Explore Any Narratives
Discover and contribute to detailed historical accounts and cultural stories. Share your knowledge and engage with enthusiasts worldwide.
Henri Poincaré, a towering figure in the annals of mathematics and physics, remains one of the most influential scientists of the late 19th and early 20th centuries. Born in 1854 in Nancy, France, Poincaré's contributions spanned multiple disciplines, earning him the title of the last universal mathematician. His work laid the groundwork for modern chaos theory, topology, and even relativity, making him a pivotal figure in the transition from classical to modern science.
Poincaré's genius was not confined to a single field. He made groundbreaking advancements in celestial mechanics, differential equations, and algebraic geometry, while also contributing to philosophy and physics. His ability to synthesize complex ideas and apply them across disciplines set him apart from his contemporaries. Today, his theories continue to influence cutting-edge research in dynamical systems, quantum mechanics, and cosmology.
Henri Poincaré was born on April 29, 1854, into a family of intellectuals and professionals. His father, Léon Poincaré, was a prominent physician, and his cousin, Raymond Poincaré, later became the President of France. From an early age, Poincaré exhibited exceptional intellectual abilities, particularly in mathematics. Despite suffering from diphtheria as a child, which temporarily impaired his physical abilities, his mental prowess remained unscathed.
Poincaré's formal education began at the Lycée in Nancy, where he excelled in all subjects, particularly mathematics. His teachers quickly recognized his extraordinary talent, and by the age of 17, he had already begun to make original contributions to the field. In 1873, he entered the École Polytechnique, one of France's most prestigious institutions, where he studied under some of the leading mathematicians of the time.
After graduating from the École Polytechnique, Poincaré continued his studies at the École des Mines, where he earned his engineering degree in 1879. That same year, he completed his doctorate in mathematics at the University of Paris, with a dissertation on partial differential equations. His thesis was so impressive that it immediately established him as a rising star in the mathematical community.
Poincaré's academic career took off rapidly. In 1879, he accepted a position as a professor at the University of Caen, where he taught for two years before moving to the University of Paris (Sorbonne) in 1881. At the Sorbonne, he spent the remainder of his career, producing an astonishing volume of work that would shape the future of mathematics and physics.
Poincaré's contributions to mathematics are vast and varied, but several key areas stand out for their lasting impact. His work in topology, differential equations, and celestial mechanics revolutionized these fields and laid the foundation for modern mathematical research.
One of Poincaré's most famous contributions is the Poincaré Conjecture, which he formulated in 1904. This conjecture, which deals with the characterization of the three-dimensional sphere, remained one of the most significant unsolved problems in mathematics for nearly a century. The conjecture states:
"Any simply connected, closed three-dimensional manifold is homeomorphic to the three-dimensional sphere."
The conjecture's complexity stumped mathematicians for decades, but it was finally proven by Grigori Perelman in 2002–2003, using techniques from geometric analysis and Ricci flow. Perelman's proof was so groundbreaking that it earned him the Fields Medal in 2006, though he famously declined the award.
In 1889, Poincaré won the prestigious King Oscar II Prize for his work on the three-body problem, a fundamental issue in celestial mechanics that seeks to predict the motion of three celestial bodies interacting through gravity. His memoir on the subject introduced several groundbreaking concepts, including:
Although Poincaré's original memoir contained a critical error, his corrected work laid the foundation for the study of nonlinear dynamics and chaotic systems. Today, his ideas are applied in fields ranging from climate modeling to fluid dynamics and astrophysics.
Poincaré's influence extended beyond pure mathematics into the realm of physics, where his ideas helped shape the development of modern theoretical frameworks. His work on electrodynamics and relativity was particularly influential, providing key insights that would later be expanded upon by Albert Einstein.
Between 1905 and 1906, Poincaré independently derived several foundational concepts of special relativity, including:
Poincaré's contributions to relativity were so significant that Einstein himself acknowledged his debt to Poincaré's ideas. While Einstein is often credited with the development of special relativity, Poincaré's work provided critical mathematical and conceptual groundwork.
In addition to his mathematical and scientific contributions, Poincaré was a profound thinker in the philosophy of science. He is best known for his advocacy of conventionalism, the idea that scientific theories are not absolute truths but rather useful conventions that help us understand the world. Poincaré argued that:
Poincaré's philosophical views continue to resonate in contemporary debates about the nature of mathematical and scientific knowledge. His emphasis on intuition and practicality has influenced generations of mathematicians and philosophers, shaping the way we think about the relationship between theory and reality.
Henri Poincaré's legacy is one of unparalleled intellectual achievement and interdisciplinary innovation. His work in mathematics, physics, and philosophy has left an indelible mark on the scientific community, influencing everything from chaos theory to relativity. In the next part of this series, we will delve deeper into Poincaré's specific contributions to topology, celestial mechanics, and his enduring impact on modern science.
Henri Poincaré's contributions to topology and algebraic geometry fundamentally transformed these fields, introducing concepts that remain central to modern mathematics. His work in topology, in particular, laid the groundwork for the study of manifolds and homotopy theory, areas that continue to drive research in both pure and applied mathematics.
Poincaré is often credited with founding the field of algebraic topology, a branch of mathematics that uses tools from abstract algebra to study topological spaces. His 1895 paper, Analysis Situs, introduced several key concepts, including:
These ideas were revolutionary because they provided a rigorous mathematical framework for studying shapes and spaces that defied traditional geometric analysis. Poincaré's approach allowed mathematicians to explore properties of spaces that remain unchanged under continuous deformations, such as stretching or bending, but not tearing or gluing.
The impact of Poincaré's topological innovations extends far beyond pure mathematics. In theoretical physics, his ideas have been applied to the study of string theory, quantum field theory, and condensed matter physics. For example, the concept of topological invariants is crucial in understanding the behavior of topological insulators, materials that conduct electricity on their surfaces but not through their interiors.
In addition, Poincaré's work on algebraic geometry provided new methods for solving systems of polynomial equations, which are fundamental in cryptography and computational algebra. His 1910–1911 proofs in algebraic geometry demonstrated the power of combining geometric intuition with algebraic techniques, a approach that continues to inspire mathematicians today.
Another cornerstone of Poincaré's legacy is the Poincaré Recurrence Theorem, a fundamental result in the study of dynamical systems. This theorem states that in a conservative system with a finite volume of phase space, almost every trajectory will eventually return arbitrarily close to its initial position. The theorem has profound implications for our understanding of statistical mechanics and ergodic theory.
The Recurrence Theorem can be summarized as follows:
"In a system where energy and volume are conserved, and where the system is bounded, any state that the system can reach will be revisited infinitely often, given enough time."
This idea challenges the notion of irreversibility in physical systems, suggesting that even in chaotic systems, certain patterns will repeat over time. Poincaré's theorem was a direct response to the second law of thermodynamics, which posits that entropy in a closed system tends to increase over time, leading to a state of maximum disorder.
The Recurrence Theorem has had a lasting impact on statistical mechanics, particularly in the study of ergodic systems, where the system's trajectory eventually explores all possible states consistent with its energy. This concept is crucial for understanding the behavior of gases and other complex systems where individual particle interactions are too numerous to track.
In chaos theory, the Recurrence Theorem highlights the unpredictable yet deterministic nature of chaotic systems. While Poincaré's work on the three-body problem showed that small changes in initial conditions can lead to vastly different outcomes, the Recurrence Theorem suggests that, over infinite time, the system will return to a state arbitrarily close to its starting point. This duality—between unpredictability and recurrence—remains a central theme in the study of dynamical systems.
Henri Poincaré's contributions to physics are as significant as his mathematical achievements. His work on electrodynamics and relativity provided critical insights that shaped the development of modern physics, influencing figures like Albert Einstein and Hendrik Lorentz.
In the early 1900s, Poincaré was deeply engaged in the study of electromagnetic theory, particularly the work of James Clerk Maxwell and Hendrik Lorentz. He recognized that the equations governing electromagnetism should remain unchanged under certain transformations, a principle that would later become a cornerstone of special relativity.
Poincaré's 1905 paper, On the Dynamics of the Electron, introduced the concept of the Lorentz group, a set of transformations that preserve the form of Maxwell's equations. He also proposed that the speed of light is a universal constant, a idea that Einstein would later incorporate into his theory of relativity. Poincaré's work demonstrated that the laws of physics should be covariant—meaning they retain their form—under these transformations, a principle that is fundamental to modern physics.
Poincaré was among the first to explore the implications of time dilation, a phenomenon where time appears to pass more slowly for an object in motion relative to a stationary observer. He introduced the twin paradox, a thought experiment where one twin travels at near-light speed and returns to find the other twin has aged more. This paradox illustrates the relativistic effects of time and has become a staple in discussions of special relativity.
Additionally, Poincaré's work on the geometry of spacetime anticipated Einstein's general theory of relativity. He suggested that the three dimensions of space and the one dimension of time could be treated as a single, four-dimensional continuum, an idea that Einstein would later formalize in his theory of general relativity. Poincaré's insights into the interplay between space and time were groundbreaking, paving the way for a new understanding of the universe.
Beyond his technical contributions, Poincaré was a profound thinker in the philosophy of mathematics and science. His views on intuition, conventionalism, and the nature of mathematical truth have had a lasting impact on how we understand the development and application of scientific theories.
Poincaré was a strong advocate for the role of intuition in mathematical discovery. He believed that while formal proofs and logical rigor are essential, the initial spark of mathematical insight often comes from an intuitive grasp of the problem. In his 1908 book, Science and Method, he wrote:
"It is by logic that we prove, but by intuition that we discover."
This emphasis on intuition was a response to the growing trend of formalism in mathematics, which sought to reduce all mathematical truths to purely logical statements. Poincaré argued that such an approach ignored the creative and often non-linear process of mathematical discovery, where intuition guides the mathematician toward meaningful problems and solutions.
Poincaré is perhaps best known for his philosophy of conventionalism, which posits that scientific theories and mathematical principles are not absolute truths but rather useful conventions that help us organize and understand the world. He argued that:
This view challenged the prevailing notion that scientific theories are direct reflections of reality. Instead, Poincaré suggested that they are tools that allow us to make sense of complex phenomena. His conventionalism has influenced later philosophers of science, including Thomas Kuhn and Paul Feyerabend, who explored the role of paradigms and scientific revolutions in shaping our understanding of the world.
Henri Poincaré's contributions to mathematics, physics, and philosophy are nothing short of revolutionary. His work in topology, chaos theory, and relativity laid the foundation for many of the scientific advancements of the 20th and 21st centuries. In the final part of this series, we will explore Poincaré's enduring legacy, his influence on contemporary science, and the ongoing relevance of his ideas in today's research.
Henri Poincaré's influence extends far beyond his lifetime, shaping the trajectory of mathematics, physics, and philosophy in profound ways. His ideas continue to inspire researchers, and his theories remain foundational in fields ranging from chaos theory to quantum mechanics. This section explores how Poincaré's work has stood the test of time and continues to drive innovation in contemporary science.
Poincaré's groundbreaking work on the three-body problem and chaos theory has had a lasting impact on modern science. His discovery of homoclinic points and the unpredictability of certain dynamical systems laid the foundation for what we now recognize as deterministic chaos. Today, chaos theory is applied in diverse fields such as:
Poincaré's insights into chaos have also influenced the development of fractal geometry, a field that studies complex, self-similar structures found in nature. His work remains a cornerstone of modern nonlinear dynamics, guiding researchers as they explore the boundaries between order and disorder.
Poincaré's contributions to topology have found unexpected applications in theoretical physics, particularly in the study of topological phases of matter. These phases, which include topological insulators and quantum Hall systems, exhibit properties that are robust against local perturbations, making them ideal for applications in quantum computing and spintronics.
The Poincaré conjecture, though proven by Grigori Perelman, continues to inspire research in higher-dimensional geometry and string theory. In string theory, the topology of Calabi-Yau manifolds—complex, multi-dimensional shapes—plays a crucial role in determining the properties of the universe. Poincaré's early work on manifolds and homotopy theory provided the mathematical framework that makes such explorations possible.
While Albert Einstein is often credited with the development of special relativity, Poincaré's contributions were instrumental in shaping the theory. His work on the Lorentz transformations and the principle of relativity provided the mathematical foundation that Einstein built upon. This section examines how Poincaré's ideas continue to resonate in modern physics.
Poincaré's ability to bridge mathematics and physics was one of his greatest strengths. His work on electrodynamics and the geometry of spacetime anticipated many of the concepts that would later become central to Einstein's general theory of relativity. Key areas where Poincaré's influence is still felt include:
Poincaré's emphasis on the unification of physical laws also foreshadowed the modern quest for a theory of everything, which seeks to reconcile quantum mechanics and general relativity into a single, coherent framework.
Poincaré's philosophical views, particularly his advocacy for conventionalism and the role of intuition in scientific discovery, continue to shape debates in the philosophy of science. His ideas challenge the notion that scientific theories are objective truths, instead suggesting that they are human constructs shaped by our need to make sense of the world.
In contemporary discussions, Poincaré's conventionalism is often contrasted with scientific realism, the view that scientific theories describe reality as it truly is. This debate remains relevant in fields such as quantum mechanics, where interpretations like the Copenhagen interpretation and many-worlds theory reflect different philosophical perspectives on the nature of reality.
Additionally, Poincaré's emphasis on intuition has influenced modern approaches to mathematical education and problem-solving. Educators and researchers alike recognize the importance of fostering intuitive understanding alongside formal training, a balance that Poincaré championed throughout his career.
The practical applications of Poincaré's theories are evident in many of today's technological advancements. From artificial intelligence to space exploration, his ideas continue to drive innovation and discovery. This section highlights some of the most notable examples of Poincaré's enduring influence.
Poincaré's work on dynamical systems and chaos theory has found applications in machine learning and artificial intelligence. Techniques inspired by his theories are used to model complex, nonlinear systems, such as:
Poincaré's emphasis on intuition also resonates in the development of AI systems, where human-like reasoning and problem-solving skills are increasingly valued.
In the field of astrophysics, Poincaré's contributions to celestial mechanics remain indispensable. His work on the three-body problem is used to model the interactions between stars, planets, and other celestial bodies, helping scientists understand the dynamics of solar systems and galaxies.
Poincaré's insights into chaotic systems are also crucial for space mission planning. For example, the Lagrange points—regions in space where the gravitational forces of two large bodies balance out—are used to position satellites and space telescopes. These points, first studied by Poincaré, are essential for missions like the James Webb Space Telescope, which relies on them to maintain its orbit.
Henri Poincaré's legacy is one of unparalleled intellectual brilliance and interdisciplinary innovation. His contributions to mathematics, physics, and philosophy have left an indelible mark on the scientific community, influencing generations of researchers and shaping the course of modern science. From his foundational work in topology and chaos theory to his groundbreaking insights into relativity and the philosophy of science, Poincaré's ideas continue to inspire and challenge us.
As we reflect on Poincaré's achievements, several key takeaways emerge:
In a world where science and technology are advancing at an unprecedented pace, Poincaré's legacy serves as a reminder of the power of curiosity, creativity, and interdisciplinary collaboration. His ideas continue to guide researchers as they explore the frontiers of knowledge, from the depths of quantum mechanics to the vast expanse of the cosmos. As we look to the future, we can be certain that the genius of Henri Poincaré will continue to illuminate the path forward, inspiring new generations to push the boundaries of what is possible.
In the words of Poincaré himself:
"Science is built up with facts, as a house is with stones. But a collection of facts is no more a science than a heap of stones is a house."
This sentiment captures the essence of Poincaré's approach to science—a blend of rigorous analysis, creative insight, and a deep appreciation for the interconnectedness of all knowledge. His legacy is not just a collection of theories and proofs but a testament to the enduring power of human intellect and imagination.
Your personal space to curate, organize, and share knowledge with the world.
Discover and contribute to detailed historical accounts and cultural stories. Share your knowledge and engage with enthusiasts worldwide.
Connect with others who share your interests. Create and participate in themed boards about any topic you have in mind.
Contribute your knowledge and insights. Create engaging content and participate in meaningful discussions across multiple languages.
Already have an account? Sign in here
Émile Borel: A Pioneering Mathematician and Physicist The Early Life and Education of Émile Borel Émile Borel, born on...
View Board
Explore the remarkable legacy of Henri Cartan, the pioneering mathematician whose groundbreaking contributions to algebr...
View Board
Isaac Newton was a pioneering scientist whose laws of motion and universal gravitation revolutionized our understanding ...
View Board
> **Meta Description:** Explore the life and legacy of Albert Einstein, the genius who reshaped physics with relativity,...
View Board
Discover the life of Aldo Pontremoli, a pioneering Italian physicist who founded Italy's first physics institute and joi...
View Board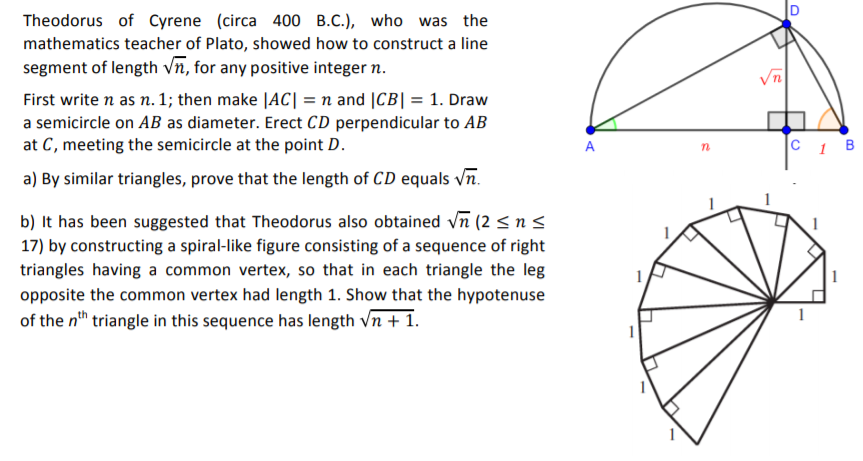
Theodorus of Cyrene, the ancient Greek mathematician and Plato's teacher, revolutionized geometry with his work on irrat...
View Board
Jean Baptiste Joseph Delambre: A Life of Astronomical Pursuits The Early Life and Education Jean Baptiste Joseph Delam...
View Board
Max Born was a renowned theoretical physicist and Nobel laureate known for his statistical interpretation of quantum mec...
View Board
Henri Lebesgue: The Mathematician Who Revolutionized Integration Henri Lebesgue was a French mathematician whose ground...
View Board
Discover how Pierre-Simon Laplace revolutionized science with his groundbreaking work in mathematics, astronomy, and pro...
View Board
Explore the life of Paul Painlevé, a groundbreaking mathematician and innovative political leader, whose dual legacy in ...
View Board
George Gamow: The Unbelievable Journey of a Theoretical Physicist and Cosmologist The Enigmatic Man Behind the Cosmic B...
View Board
John von Neumann, the 20th-century polymath, revolutionized computing, game theory, nuclear physics, and AI. Explore his...
View Board
John Napier, a Scottish mathematician, invented logarithms, revolutionizing calculations and paving the way for signific...
View Board
Discover the life and work of Albert Einstein, a renowned physicist and one of the most influential scientists in histor...
View Board
Arthur Eddington: Pioneering Relativity and Stellar Science Arthur Stanley Eddington stands as one of the most influenti...
View Board
Discover the life and legacy of Gaston Julia, the brilliant mathematician who pioneered fractals and Julia sets, shaping...
View Board
Discover Jean-Baptiste Joseph Delambre, the pioneering astronomer of the 18th century who revolutionized geodesy and cel...
View Board
**Meta Description:** Explore the life and legacy of Pierre-Simon Laplace, the visionary mathematician who shaped cele...
View Board
"Discover Pierre-Simon Laplace's legacy: the 'French Newton' who revolutionized math, astronomy & probability. Learn his...
View Board
Comments