Explore Any Narratives
Discover and contribute to detailed historical accounts and cultural stories. Share your knowledge and engage with enthusiasts worldwide.
Henri Lebesgue was a French mathematician whose groundbreaking work on measure theory and the Lebesgue integral transformed the landscape of real analysis, probability, and Fourier series. His 1902 dissertation, Intégrale, longueur, aire, introduced a new way of understanding integration that went beyond the limitations of the Riemann integral, paving the way for modern mathematical analysis.
Henri Léon Lebesgue was born on June 28, 1875, in Beauvais, France. From an early age, he displayed a keen interest in mathematics, which led him to pursue higher education at the prestigious École Normale Supérieure in Paris. There, he studied under the guidance of Émile Borel, whose work on measure theory would later influence Lebesgue’s own contributions.
After graduating, Lebesgue began his teaching career at the Lycée Central in Nancy in 1899, where he taught until 1902. During this period, he developed the foundational ideas that would culminate in his revolutionary dissertation.
Before Lebesgue’s work, the Riemann integral, developed by Bernhard Riemann, was the standard method for integration. However, the Riemann integral had significant limitations, particularly in dealing with discontinuous functions. This restriction hindered progress in areas such as Fourier series and probability theory, where discontinuous functions frequently arise.
Lebesgue recognized these limitations and sought to develop a more general and flexible approach to integration. His solution was to shift the focus from the domain of the function to its codomain, a radical departure from previous methods.
In 1902, Lebesgue published his dissertation, Intégrale, longueur, aire, which introduced the concept of the Lebesgue integral. This work was groundbreaking for several reasons:
Lebesgue’s approach involved defining the measure of a set first and then constructing the integral based on these measures. This method allowed for the integration of functions that were not continuous, a significant advancement over the Riemann integral.
In 1901, Lebesgue published a paper titled Sur une généralisation de l'intégrale définie in the Comptes Rendus. This paper laid the groundwork for his later dissertation by introducing the idea of generalizing the definite integral to handle more complex functions.
By 1905, Lebesgue had made significant progress in applying his integral to Fourier series. He proved that term-by-term integration was valid for bounded Lebesgue-integrable functions, a result that had far-reaching implications for the study of these series. Additionally, his work contributed to the Riemann–Lebesgue lemma, a key result in the analysis of Fourier coefficients.
In 1910, Lebesgue extended his theory of integration and differentiation to n-dimensional space. This generalization was crucial for the development of multivariable calculus and had applications in physics and engineering. He also introduced the concept of countably additive set functions, which became a cornerstone of modern measure theory.
The Lebesgue Differentiation Theorem, proved in 1912, is one of Lebesgue’s most enduring contributions. This theorem states that for a measurable function, the derivative exists almost everywhere, providing a deep connection between integration and differentiation. It remains a fundamental result in real analysis.
Lebesgue’s contributions to mathematics were widely recognized during his lifetime. He received several prestigious awards, including:
These awards underscored the significance of his work and its impact on the mathematical community. Lebesgue’s theories were not only theoretical breakthroughs but also had practical applications in various fields, from probability to partial differential equations.
Lebesgue’s work laid the foundation for several key areas of modern mathematics. His measure theory and Lebesgue integral are central to:
By 1922, Lebesgue had published nearly 90 papers, many of which were foundational to modern mathematical research. His later work focused on pedagogy and the history of mathematics, ensuring that his ideas were accessible to future generations of mathematicians.
Lebesgue’s dissertation is often cited as one of the finest in the history of mathematics, and his theories remain a core part of graduate curricula in mathematics and applied sciences. His influence extends beyond pure mathematics, impacting fields such as data science, statistics, and machine learning, where measure-theoretic probability plays a crucial role.
Henri Lebesgue passed away on July 26, 1941, but his contributions to mathematics continue to resonate. His development of the Lebesgue integral and measure theory revolutionized the way mathematicians approach integration and analysis. Today, his ideas are foundational to numerous fields, from probability to data science, demonstrating the enduring power of his work.
In the next part of this series, we will delve deeper into Lebesgue’s specific contributions to Fourier series, probability theory, and his later work in geometry and topology. Stay tuned for a more detailed exploration of his mathematical achievements and their modern applications.
Henri Lebesgue made groundbreaking contributions to Fourier series, a field that had long puzzled mathematicians due to issues of convergence and representation. His work provided the rigorous foundation needed to address these challenges, particularly through his development of the Lebesgue integral.
One of Lebesgue’s most significant achievements in this area was his 1905 proof that term-by-term integration is valid for bounded Lebesgue-integrable functions. This result was crucial because it allowed mathematicians to integrate Fourier series term by term, a process that was not generally valid under the Riemann integral.
His work also contributed to the Riemann–Lebesgue lemma, which states that the Fourier coefficients of a Lebesgue-integrable function tend to zero as the frequency increases. This lemma is fundamental in the study of Fourier analysis and has applications in signal processing and partial differential equations.
Lebesgue’s theories have had a lasting impact on harmonic analysis and functional analysis. His approach to integration allowed for the study of more complex functions, including those with discontinuities and infinite variations. This flexibility has been essential in:
Measure theory, as developed by Lebesgue, became the cornerstone of modern probability theory. Before Lebesgue, probability lacked a rigorous mathematical foundation, relying heavily on intuitive notions of likelihood and expectation. Lebesgue’s work provided the tools needed to formalize these concepts.
In 1933, Andrey Kolmogorov used Lebesgue’s measure theory to develop the axiomatic foundation of probability. Kolmogorov’s axioms, which define probability spaces in terms of measure spaces, are directly inspired by Lebesgue’s work. This axiomatization allowed probability to be treated as a rigorous branch of mathematics.
Key concepts in Kolmogorov’s framework, such as probability measures and random variables, are defined using Lebesgue’s theory. For example:
The influence of Lebesgue’s measure theory extends to statistics and data science. Modern statistical methods, such as Bayesian inference and stochastic processes, rely on measure-theoretic probability. For instance:
While Lebesgue is best known for his work in real analysis and measure theory, he also made significant contributions to geometry and topology. His later work explored the connections between these fields and his theories of integration.
In 1911, Lebesgue introduced the concept of the covering dimension, a topological invariant that generalizes the notion of dimension for arbitrary topological spaces. This concept, now known as the Lebesgue covering dimension, is defined using open covers of a space and has become a fundamental tool in dimension theory.
The Lebesgue covering dimension is particularly important in:
In 1921, Lebesgue proved a theorem on dimensional invariance, showing that the dimension of a topological space is a well-defined invariant. This result resolved a long-standing question in topology and provided a rigorous foundation for the study of dimensions in abstract spaces.
Lebesgue also contributed to the study of tiling problems, which involve covering a space with non-overlapping shapes. His work in this area has applications in crystallography and materials science, where tiling patterns are used to model the structure of crystals and other periodic structures.
In the later years of his career, Lebesgue shifted his focus to mathematical education and the history of mathematics. He believed that understanding the historical development of mathematical ideas was crucial for both teaching and research.
Lebesgue was a strong advocate for rigorous mathematical education. He emphasized the importance of teaching students the foundational concepts of analysis and measure theory, rather than relying on intuitive or heuristic methods. His educational writings include:
Lebesgue’s approach to education influenced generations of mathematicians, shaping the way real analysis and measure theory are taught in universities today.
Lebesgue also wrote extensively on the history of mathematics, particularly the development of integration and analysis. His historical works provide valuable insights into the evolution of mathematical thought, from the early days of Newton and Leibniz to the modern era.
One of his notable historical contributions was his analysis of the work of Bernhard Riemann and Camille Jordan. Lebesgue highlighted the limitations of their approaches to integration and measure, showing how his own theories addressed these shortcomings. His historical commentary remains a valuable resource for understanding the progression of mathematical ideas.
Henri Lebesgue’s work has had a profound and lasting impact on mathematics. His development of the Lebesgue integral and measure theory revolutionized real analysis, probability, and Fourier analysis. These theories are now fundamental to numerous fields, from physics and engineering to data science and machine learning.
Lebesgue’s contributions extended beyond pure mathematics. His work in geometry and topology provided new tools for understanding complex structures, while his educational and historical writings ensured that his ideas would be accessible to future generations.
Today, Lebesgue’s theories are taught in universities worldwide, and his name is synonymous with rigor and innovation in mathematical analysis. His legacy continues to inspire mathematicians and scientists, demonstrating the enduring power of his contributions.
In the final part of this series, we will explore Lebesgue’s influence on modern computational mathematics and his role in shaping the future of mathematical research. Stay tuned for a deeper dive into his lasting impact on the world of mathematics.
Henri Lebesgue’s theories continue to shape computational mathematics, particularly in areas requiring precise handling of uncertainty and complex functions. His Lebesgue integral provides the mathematical foundation for numerical analysis and statistical computing, enabling algorithms to process data with discontinuities and irregular distributions.
In numerical integration, Lebesgue’s approach allows for the approximation of integrals over functions that traditional methods struggle with. This is critical in:
Lebesgue’s work underpins machine learning through its reliance on measure-theoretic probability. Key examples include:
Modern algorithms frequently encounter non-smooth data, making Lebesgue’s tools indispensable for rigorous analysis and optimization.
As mathematics evolves, Lebesgue’s ideas remain at the forefront of interdisciplinary research. His theories continue to inspire new developments in areas such as quantum computing and topological data analysis.
Researchers are exploring how Lebesgue’s concepts can address challenges in:
"Lebesgue’s integral is not just a tool—it is the language through which modern mathematics speaks to complexity."
Academic institutions worldwide continue to honor Lebesgue through:
These efforts ensure that Lebesgue’s vision of rigorous, generalizable mathematics remains accessible to future generations.
Henri Lebesgue transformed mathematics by redefining how we approach integration, measurement, and analysis. His 1902 dissertation not only generalized the Riemann integral but also laid the groundwork for modern probability theory, Fourier analysis, and functional analysis.
Key takeaways from his legacy include:
Today, Lebesgue’s ideas permeate fields from to , proving that his work transcends theoretical mathematics. As new challenges arise, his theories continue to offer solutions, demonstrating the enduring power of his insights.
In closing, Henri Lebesgue’s legacy is a testament to the profound impact one mind can have on an entire discipline. His rigorous, innovative approach not only solved longstanding problems but also opened doors to future discoveries. As mathematics progresses, Lebesgue’s name will remain synonymous with the depth, beauty, and utility of modern mathematical thought.




Your personal space to curate, organize, and share knowledge with the world.
Discover and contribute to detailed historical accounts and cultural stories. Share your knowledge and engage with enthusiasts worldwide.
Connect with others who share your interests. Create and participate in themed boards about any topic you have in mind.
Contribute your knowledge and insights. Create engaging content and participate in meaningful discussions across multiple languages.
Already have an account? Sign in here
Émile Borel: A Pioneering Mathematician and Physicist The Early Life and Education of Émile Borel Émile Borel, born on...
View Board
John Napier, a Scottish mathematician, invented logarithms, revolutionizing calculations and paving the way for signific...
View Board
Isaac Newton was a pioneering scientist whose laws of motion and universal gravitation revolutionized our understanding ...
View Board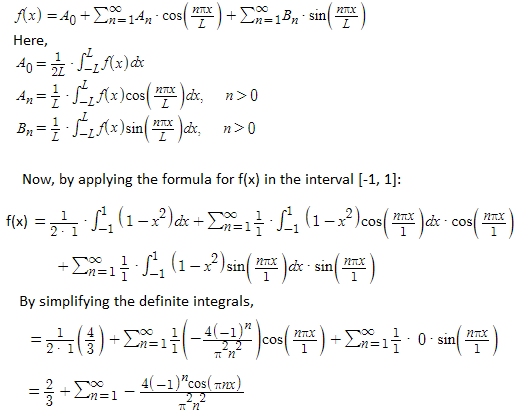
Explore the life and groundbreaking innovations of Jean-Baptiste Joseph Fourier, the French mathematician and physicist ...
View Board
Explore the life and legacy of Jules Henri Poincaré, a prodigy whose innovative work bridged mathematics and physics. Di...
View Board
"Explore Henri Poincaré's groundbreaking work in math, physics, and philosophy, shaping modern science through chaos the...
View Board
Discover how Isaac Newton revolutionized science with his laws of motion, universal gravitation, and optics. Explore his...
View Board
Explore the remarkable legacy of Henri Cartan, the pioneering mathematician whose groundbreaking contributions to algebr...
View Board
"Explore the Omicron symbol (Ο, ο) in math & science! Learn its role in Big O notation, algorithm analysis, and more. Di...
View Board
Explore the inspirational journey of Émile Picard, a pioneering French mathematician whose groundbreaking work in comple...
View Board
John von Neumann, the 20th-century polymath, revolutionized computing, game theory, nuclear physics, and AI. Explore his...
View Board
Discover the life and work of Albert Einstein, a renowned physicist and one of the most influential scientists in histor...
View Board
Explore the life and legacy of Dmitri Mendeleev, the visionary architect of the periodic table. Discover how his groundb...
View Board
Descubre cómo Henri Lebesgue revolucionó el análisis matemático con su integral, superando límites clásicos y sentando b...
View Board
**Meta Description:** Explore the life and legacy of Hermann von Helmholtz, the 19th-century polymath who revolutionized...
View Board
> **Meta Description:** Explore the life and legacy of Albert Einstein, the genius who reshaped physics with relativity,...
View Board
"Explore Jacques Hadamard's legacy: Prime Number Theorem proof, functional analysis, and impact on modern tech. Discover...
View Board
Discover the life and legacy of Gaston Julia, the brilliant mathematician who pioneered fractals and Julia sets, shaping...
View Board
768 **Meta Description:** Explore the life of Enrico Fermi, the architect of the nuclear age. From quantum theory to th...
View Board
Explore the monumental legacy of Ernest Rutherford, the father of nuclear physics, in our insightful article. Delve into...
View Board
Comments