Explore Any Narratives
Discover and contribute to detailed historical accounts and cultural stories. Share your knowledge and engage with enthusiasts worldwide.
The intriguing phrase Zak-Antamar-H-Symbolh-enos-Ma8hmatikoy-Oramatisth invites a deep dive into the world of mathematical notation and its visionaries. This phrase translates from Greek as "Zak-Antamar: The Symbol of a Mathematical Visionary," suggesting a focus on the powerful intersection of mathematical symbols and the thinkers who revolutionize them. While not a widely recognized proper name, the concept serves as a perfect lens to examine how symbolic innovation has fundamentally shaped mathematical progress. This article explores the history, significance, and future of the symbols that underpin mathematical thought.
Mathematical symbols are the fundamental building blocks for expressing complex ideas with precision and clarity. A mathematical symbol is a grapheme used to represent objects, operations, or relations. Without a standardized glossary of mathematical symbols, the global collaboration that defines modern mathematics would be impossible. These symbols form a universal language, allowing ideas discovered in one part of the world to be seamlessly shared, challenged, and built upon by scholars everywhere.
The history of mathematics is filled with examples where a new notation convention catalyzed an entire field. The adoption of symbolic algebra in the 16th and 17th centuries, pioneered by mathematicians like François Viète, freed mathematics from verbose descriptions. This allowed for the manipulation of abstract equations and paved the way for calculus. The notation we use today is not static; it evolves within subfields like category theory to express increasingly abstract concepts.
Notation is convention-driven—symbols acquire meaning by community use. This collective agreement is what makes mathematics a truly cumulative science.
While the name Zak Antamar may not appear in historical records, many true visionaries have left an indelible mark through their use of symbols. Figures like Évariste Galois introduced notations for group theory that unlocked the solvability of polynomial equations. Emmy Noether's work in abstract algebra relied on and advanced symbolic clarity, influencing countless physicists and mathematicians. Their legacies demonstrate how a mathematical visionary often creates or refines the symbolic toolkit for future generations.
The impact is profound. Srinivasa Ramanujan, with his intuitive and sometimes unconventional notation, produced thousands of groundbreaking theorems. The development of function notation by Leonhard Euler provided a framework for analysis that is still used today. These pioneers did not just discover new truths; they forged the symbols needed to convey them, much like the concept embodied in our central phrase.
A major modern trend is the digitization and standardization of mathematical symbols. The Unicode Standard and MathML are critical to this evolution. They ensure that specialized symbols render correctly across all digital platforms, from academic papers to educational websites.
The idea of a mathematical visionary's symbol also extends across cultures. While Western mathematics heavily employs Greek and Latin letters, other traditions have developed rich, localized notation systems. For instance, Modern Arabic mathematical notation adapts core concepts to Arabic script and right-to-left layout. This localization is crucial for pedagogy and demonstrates that the conceptual meaning of a symbol can transcend its graphical form.
This cultural dimension highlights an important truth. The essence of a mathematical idea is separate from the symbol used to denote it. A community's choice of notation—whether using Greek letters or Arabic script—serves the needs of its learners and practitioners. The visionary aspect lies in creating systems that effectively communicate profound ideas within a specific cultural and linguistic context.
A rise in educational content underscores the public hunger for understanding mathematical symbols. Numerous YouTube channels, mobile apps, and online glossaries are dedicated to explaining symbols to students and enthusiasts. This aligns with the spirit of a mathematical visionary as an educator who demystifies complex notation. These resources bridge the gap between abstract symbolism and intuitive understanding, which is the first step toward future innovation.
Authoritative, aggregated quantitative data on symbol usage across papers or curricula are scarce, but the proliferation of educational media clearly indicates high demand for this knowledge.
As we conclude this first part, we have established the critical importance of symbols in mathematics. We have seen their historical power, their digital evolution, and their cultural variations. In the next section, we will delve deeper into specific symbol classes, analyze the process of symbolic innovation, and further explore the profile of a true mathematical visionary.
To understand the legacy of a mathematical visionary, one must first master the language they speak: the diverse classes of symbols. The glossary of mathematical symbols is vast, but it can be organized into functional categories. These categories include operators, relations, constants, and variables. Each class serves a distinct purpose in constructing the logical sentences that form mathematical proofs and theories.
Operators, like + (addition) and ∫ (integration), denote actions to be performed. Relation symbols, such as = (equals) and > (greater than), specify how entities compare. The power of these symbols lies in their universal recognition. A mathematician in any country instantly understands the statement “π > 3”. This universality is the bedrock upon which global mathematical research is built.
As mathematics advances into specialized domains, so too does its symbolic notation. Fields like category theory and homotopy type theory have developed intricate suites of symbols. These symbols, like arrows (→, ⇒) and diagrams, are not merely shorthand. They are essential tools for visualizing and manipulating highly abstract structures that are difficult to convey in words alone.
How does a new symbol enter the mathematical lexicon? The journey from a visionary's idea to widespread convention is rarely straightforward. Unlike a formal language with a governing body, mathematical notation evolves organically through community use and publication. A researcher might introduce a new symbol in a groundbreaking paper. Its adoption hinges on utility, clarity, and the influence of its proponent.
No single global authority changes symbol meaning frequently; developments are driven by notation conventions in subfields and digital standards.
The process is exemplified by historical cases. Gottfried Leibniz's notation for calculus (dx, ∫) competed with Isaac Newton's fluxions. Leibniz's more suggestive symbols ultimately prevailed in most of the world due to their intuitive power. This shows that a successful symbolic innovation often feels natural and reveals underlying structure, a hallmark of visionary thinking.
In the modern era, standardizing a new symbol faces unique challenges and opportunities. Digital publishing and computational mathematics require symbols to be machine-readable. Therefore, widespread adoption often depends on inclusion in key standards.
The concept of a Zak-Antamar-H-Symbolh-enos-Ma8hmatikoy-Oramatisth invites us to look beyond the most famous names. History is filled with thinkers whose symbolic contributions were pivotal yet sometimes overlooked. George Boole's algebraic symbols for logic (∧, ∨) laid the foundation for the digital age. John Conway's notation for surreal numbers and game theory created entire new fields of study.
These visionaries share a common trait: they saw the need for a new language to describe newly discovered landscapes of thought. Their symbols acted as keys, unlocking doors for others to follow. Their work underscores that the creation of effective notation is itself a profound mathematical act, inseparable from the discovery process.
For a true mathematical visionary, symbols are not just logical tools; they are vessels for visualization. The way symbols are arranged on a page can illuminate structure and suggest new pathways. The evolution of notation for tensors, for example, from cumbersome index-laden expressions to more diagrammatic "birdtrack" notations, directly aids intuition. This visual dimension is crucial for fostering the insights that drive mathematics forward.
Modern tools amplify this. Software that dynamically links symbolic expressions to graphical representations allows students and researchers to "see" the meaning behind the symbols. This bridges the gap between abstract formalism and geometric intuition, a gap that visionary notation has always sought to close.
A powerful example of symbolic adaptation is found in Modern Arabic mathematical notation. This system adapts the core framework of Western mathematical symbols to the Arabic script and a right-to-left presentation. It is a testament to the principle that the conceptual meaning of a mathematical idea can be conveyed through different symbolic forms.
This localization has significant pedagogical impact. Students learn foundational concepts like algebra and calculus using notation that aligns with their native reading direction and script. Studies suggest this can reduce cognitive load and improve comprehension. It demonstrates how a community of educators can act as collective visionaries, tailoring the symbolic language of mathematics to serve their learners better.
Educational localization shows how symbols' appearance and directionality affect pedagogy, ensuring mathematical literacy is accessible across linguistic barriers.
While centralized, authoritative statistics on global symbol usage are scarce, analysis of large digital corpora like the arXiv preprint server provides insights. Such analyses can track the rise of specific notations within subfields. For instance, the use of the tensor product symbol (⊗) has seen a marked increase in physics and computer science papers over the last two decades, reflecting the growth of quantum information and applied category theory.
As we have seen, the world of mathematical symbols is dynamic, culturally sensitive, and deeply tied to innovation. The visionary, whether an individual like the enigmatic "Zak Antamar" or a collective of educators, plays the crucial role of a linguist, crafting the words for new ideas. In the final part, we will look toward the future, examining emerging trends in symbolic communication and the enduring quest for the perfect notation.
The trajectory of mathematical symbols points toward greater digital integration, accessibility, and perhaps even artificial intelligence-assisted innovation. The ongoing work of the Unicode Consortium and the World Wide Web Consortium (W3C) on standards like MathML 4 ensures that the digital representation of mathematics will keep pace with its conceptual growth. This future is not just about preserving old symbols but creating an ecosystem where new notations can flourish and be shared instantly across the globe.
Emerging fields like quantum computing and data science are already demanding new symbolic conventions. The need to represent quantum circuits, complex data structures, and machine learning architectures will inevitably lead to symbolic innovation. The next generation of mathematical visionaries will be those who can devise notations that are both computationally tractable and intuitively clear for human researchers. Their symbols will become the blueprints for future discoveries.
A provocative frontier is the role of artificial intelligence in notation. Could AI systems analyze mathematical structures and suggest optimal symbolic representations? Research into automated theorem proving and symbolic computation already touches on this area. An AI might propose a novel notation that minimizes cognitive load or maximizes the reveal of hidden patterns, acting as a collaborative partner in the visionary process.
Underlying the history and future of notation is a deep, almost philosophical quest: the search for a symbol that perfectly encapsulates an idea. This is the core of the Zak-Antamar-H-Symbolh-enos-Ma8hmatikoy-Oramatisth concept. A perfect symbol is elegant, memorable, and suggestive of its meaning and properties. It becomes so natural that mathematicians forget it was ever invented. The integral sign ∫ elegantly suggests summation, and the equals sign = represents balance with perfect simplicity.
The creative leap often comes from notation that clarifies structure, turning opaque complexity into navigable terrain.
This quest is never-ending because mathematics itself is never-ending. Each new abstraction, from sheaves to ∞-categories, challenges the community to find its visual and symbolic voice. The success of a notation can even be measured by how it enables further discovery. Good notation does not just describe; it inspires and guides the imagination toward new theorems and connections.
Despite trends toward standardization and digitization, the choice of symbols remains a deeply human, sometimes even aesthetic, decision. Individual mathematicians and research communities develop notational preferences and styles. These personal touches are part of the culture of mathematics. The enduring lesson from figures like Euler or Ramanujan is that personal intuition often guides the creation of the most powerful and lasting symbols.
Our exploration of the theme suggested by Zak-Antamar-H-Symbolh-enos-Ma8hmatikoy-Oramatisth reveals a fundamental truth. Mathematical symbols are not mere abbreviations. They are the very DNA of mathematical thought. They carry the genetic instructions for logic, structure, and creativity. A visionary, in this context, is a geneticist, splicing and crafting new strands of this DNA to give birth to new fields of intellectual inquiry.
The story of mathematical notation is a story of human progress. It mirrors our journey from clay tablets and verbose rhetoric to digital manuscripts and global collaboration. Each symbol added to the global glossary represents a victory for clarity over confusion, for shared understanding over isolated insight. It is a collective project spanning centuries and cultures.
Whether you are a student, an educator, or a practicing researcher, engaging deeply with mathematical symbols is essential. Here are the critical lessons from our journey:
In conclusion, the enigmatic phrase that guided this article serves as a powerful metaphor. The symbol of a mathematical visionary is more than a character on a page. It is a catalyst, a bridge, and a legacy. From the historical giants who gave us our foundational notation to the unnamed educators adapting symbols for their classrooms, visionaries understand that the medium is intimately tied to the message.
The future of mathematics depends on this continued symbolic innovation. As we tackle problems of increasing complexity in climate science, medicine, and fundamental physics, we will need new languages to describe new realities. The next great mathematical visionary might be working right now, struggling to express a revolutionary idea. Their breakthrough may come not just in a new theorem, but in the very symbol they choose to represent it—a symbol that, in time, will become obvious and indispensable to us all.
The search for the perfect symbol, the quest to be a Ma8hmatikoy Oramatisth, is ultimately the search for perfect understanding. It is a journey without a final destination, but each step forward—each new, clever, or beautifully simple symbol adopted by the community—enlarges the realm of human knowledge and connects us more deeply to the logical structure of the universe.
Your personal space to curate, organize, and share knowledge with the world.
Discover and contribute to detailed historical accounts and cultural stories. Share your knowledge and engage with enthusiasts worldwide.
Connect with others who share your interests. Create and participate in themed boards about any topic you have in mind.
Contribute your knowledge and insights. Create engaging content and participate in meaningful discussions across multiple languages.
Already have an account? Sign in here

Descubre el legado matemático de Émile Picard, visionario del siglo XIX. Explora sus teoremas, métodos y contribuciones ...
View Board
Explore Charles Hermite's key math contributions: proving e's transcendence, Hermite polynomials, and shaping quantum me...
View Board
Explore the extraordinary legacy of Charles Hermite in modern mathematics through his pioneering contributions to number...
View Board
Discover the life and legacy of Gaston Julia, the brilliant mathematician who pioneered fractals and Julia sets, shaping...
View Board
Explore the life and legacy of Jacques Hadamard, a pivotal mathematician of the 20th century whose innovations in number...
View Board
Descubre cómo Henri Lebesgue revolucionó el análisis matemático con su integral, superando límites clásicos y sentando b...
View Board
Descubre la vida y legado de Jacques Hadamard, el genio matemático francés que revolucionó el análisis matemático, demos...
View Board
Entdecken Sie das Leben und Werk von Évariste Galois, dem mathematischen Genie, das die moderne Algebra revolutionierte....
View Board
Discover Euclid, the Father of Geometry, and his timeless work *Elements*. Explore his life, groundbreaking theorems, an...
View Board
Explore the inspirational journey of Émile Picard, a pioneering French mathematician whose groundbreaking work in comple...
View Board
Explore the remarkable legacy of Henri Cartan, the pioneering mathematician whose groundbreaking contributions to algebr...
View Board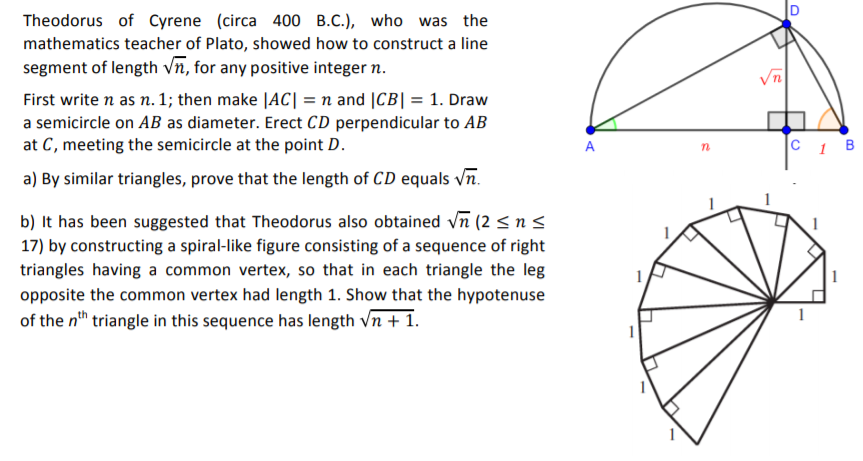
Theodorus of Cyrene, the ancient Greek mathematician and Plato's teacher, revolutionized geometry with his work on irrat...
View Board
Descubre cómo Gastón Julia revolucionó las matemáticas con sus conjuntos fractales, sentando las bases de la geometría m...
View Board
"Explore Jacques Hadamard's legacy: Prime Number Theorem proof, functional analysis, and impact on modern tech. Discover...
View Board
Descubre cómo Joseph Fourier revolucionó la ciencia con sus series matemáticas y la ecuación del calor, sentando las bas...
View Board
Mae Jemison: A Pioneering Astronaut and Champion of STEM Education The world was awe-struck when Mae Jemison became the...
View Board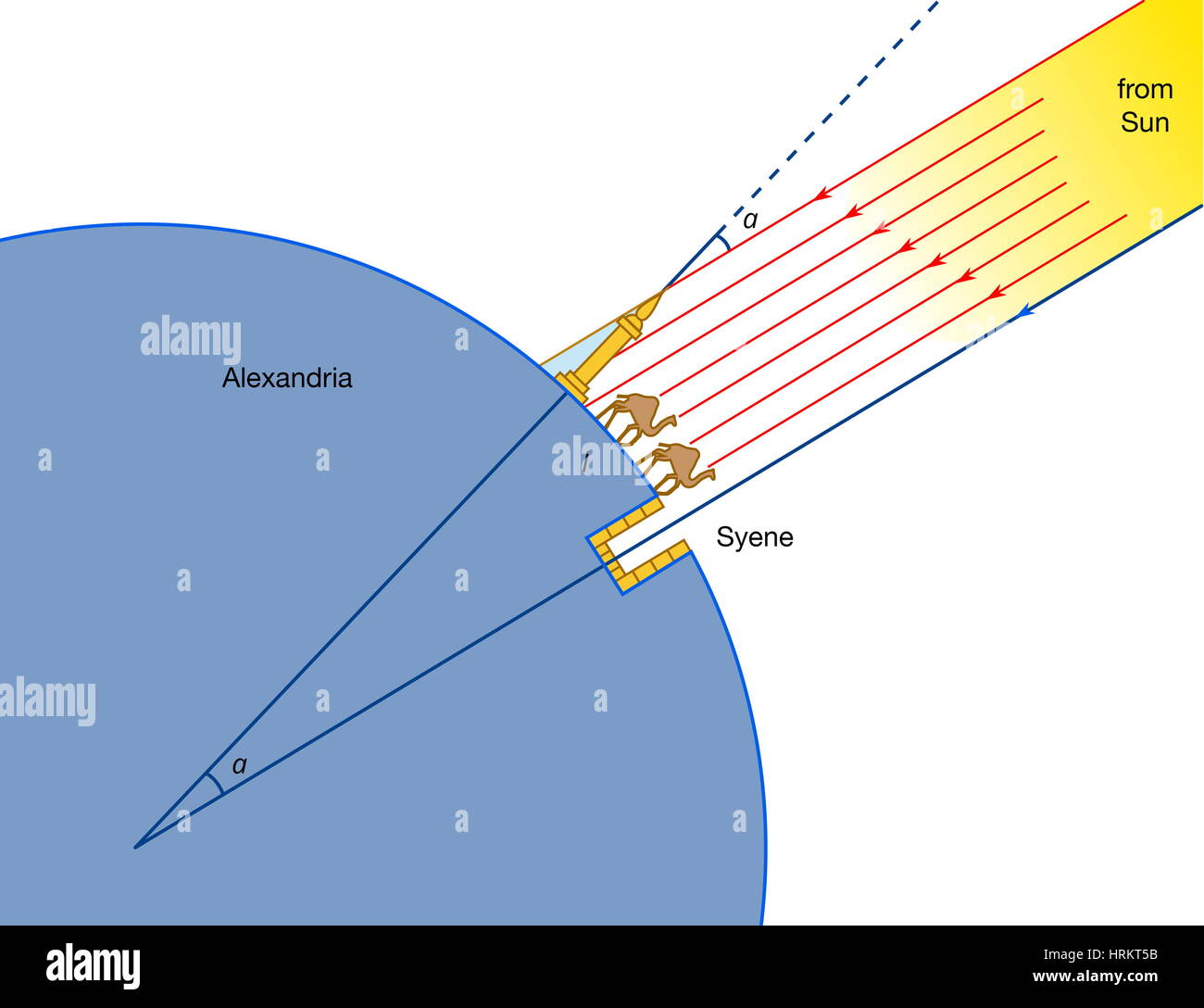
Eratosthenes: The Ptolemaic Genius of ancient Greece Eratosthenes of Cyrene (c. 276–194 BC) was not only a polymath and...
View Board
Jean Baptiste Joseph Delambre: A Life of Astronomical Pursuits The Early Life and Education Jean Baptiste Joseph Delam...
View BoardÉmile Borel: A Pioneering Mathematician and Physicist The Early Life and Education of Émile Borel Émile Borel, born on...
View Board
James Clerk Maxwell unified electricity and magnetism into a single mathematical framework, his work laying the foundati...
View Board
Comments