Explore Any Narratives
Discover and contribute to detailed historical accounts and cultural stories. Share your knowledge and engage with enthusiasts worldwide.
Jacques Hadamard fue un matemático francés cuya genialidad excepcional transformó múltiples campos del análisis matemático y dejó una huella perdurable en la ciencia. Reconocido mundialmente por probar el teorema de los números primos, su legado abarca desde ecuaciones diferenciales hasta la computación cuántica moderna. Este artículo explora la vida y las contribuciones inigualables de un genio cuyas ideas continúan resonando en el siglo XXI.
Jacques-Salomon Hadamard nació el 8 de diciembre de 1865 en Versalles, Francia. Desde una edad muy temprana, su talento intelectual fue evidente, destacando notablemente en el prestigioso Concours Général a partir de 1875. Este entorno académico riguroso fue el crisol donde se forjó su futuro como uno de los grandes matemáticos de su tiempo.
Hadamard se formó en la célebre École Normale Supérieure, donde desarrolló una profunda pasión por el análisis complejo. En 1892, obtuvo su doctorado con una tesis sobre funciones definidas por series de Taylor. El joven investigador no tardó en captar la atención de la comunidad científica, ganando el Grand Prix des Sciences Mathématiques por su ensayo sobre la función zeta de Riemann.
Este premio fue solo el comienzo de una carrera llena de logros. Su trabajo doctoral sentó las bases para sus futuras exploraciones en áreas tan diversas como las ecuaciones diferenciales y el análisis funcional. La precisión y profundidad de sus primeros trabajos ya anunciaban el genio de proporciones iniguales en el que se convertiría.
Su tesis doctoral y el ensayo premiado sobre la función zeta evidenciaron una capacidad analítica fuera de lo común, marcando el inicio de una producción científica monumental.
El año 1896 se convertiría en un hito en la historia de las matemáticas. De manera independiente a Charles-Jean de la Vallée Poussin, Jacques Hadamard consiguió demostrar el emblemático teorema de los números primos. Este resultado, largamente conjeturado, describe la distribución asintótica de los números primos.
El teorema establece formalmente que, si π(n) denota la cantidad de números primos menores o iguales a n, entonces se cumple la aproximación:
π(n) ≈ n / ln(n) a medida que n → ∞.
Esta demostración no solo resolvía uno de los problemas más importantes de la teoría de números del siglo XIX, sino que consolidó a Hadamard como una figura de primer orden en el panorama matemático mundial. El uso de métodos del análisis complejo para resolver un problema de teoría de números fue considerado una hazaña de gran ingenio.
La prueba del teorema tuvo un impacto revolucionario. Validó definitivamente la conexión profunda entre la teoría analítica de números y la función zeta de Riemann. Este logro le valió importantes reconocimientos, como el Premio Bordin en 1896, y estableció un nuevo estándar en la investigación matemática.
En 1893, tres años antes de su gran teorema, Hadamard ya había hecho otra contribución fundamental. Publicó su famosa desigualdad de Hadamard, un resultado elegante y poderoso para los determinantes de ciertas matrices. Este trabajo es la piedra angular de las ahora conocidas como matrices de Hadamard.
Una matriz de Hadamard es una matriz cuadrada cuyas entradas son +1 o -1 y cuyas filas son mutuamente ortogonales. La desigualdad establece un límite superior absoluto para el valor del determinante de una matriz con entradas complejas acotadas en módulo.
La relevancia de este descubrimiento fue más allá de las matemáticas puras. Las matrices de Hadamard encontraron aplicaciones prácticas en:
La desigualdad de 1893 demostró la capacidad de Hadamard para crear conceptos abstractos con aplicaciones prácticas de largo alcance, trascendiendo su propia época.
La vida de Jacques Hadamard estuvo profundamente entrelazada con los acontecimientos históricos de su época. En 1896, el mismo año de su gran demostración, contrajo matrimonio con su novia de infancia. Su etapa profesional en Burdeos, de 1893 a 1897, fue particularmente prolífica. Allí ocupó una cátedra de astronomía y mecánica racional y publicó la asombrosa cantidad de 29 trabajos profundos en temas muy variados.
Hadamard, de origen judío, fue un activista comprometido. Participó activamente en la defensa de Alfred Dreyfus durante el famoso caso que dividió a Francia, combatiendo el antisemitismo desde su posición de prestigio. Este compromiso social y político marcó su carácter tanto como sus logros académicos.
Su carrera docente prosiguió en instituciones de élite como la Sorbona y el Collège de France, donde sucedió al gran Henri Poincaré en la Academia de Ciencias en 1912. Sin embargo, la Segunda Guerra Mundial truncó su vida en Europa. En 1941, huyendo del régimen de Vichy, se exilió en los Estados Unidos, donde trabajó en la Universidad de Columbia. Su pensamiento, sin embargo, trascendía fronteras e influyó en movimientos posteriores como el grupo Bourbaki.
La primera parte de la vida y obra de Jacques Hadamard revela al genio matemático de proporciones iniguales que forjó herramientas abstractas con consecuencias prácticas eternas. Su dominio del análisis funcional, su rigor en la teoría de números y su creatividad inagotable son solo la introducción a un legado que continúa en pleno siglo XXI.
La vasta obra de Jacques Hadamard se extiende mucho más allá del teorema de los números primos. Sus contribuciones al análisis funcional y a la teoría de las ecuaciones diferenciales parciales fueron igualmente revolucionarias y cimentaron su estatus de pensador total en matemáticas. Su capacidad para abordar problemas fundamentales desde ángulos novedosos transformó estas disciplinas.
Una de las ideas más influyentes de Hadamard es la noción de un "problema bien planteado" en el contexto de las ecuaciones diferenciales parciales. Postuló que para que un problema matemático tenga significado físico y sea resoluble, debe cumplir tres condiciones esenciales. Esta conceptualización disciplinó el campo y guió generaciones de investigadores.
Este marco conceptual no solo fue teórico; proporcionó un criterio riguroso para evaluar la validez de modelos en física matemática e ingeniería. Muchos problemas que antes parecían intratables pudieron ser reformulados siguiendo los principios de Hadamard.
La definición de problemas bien planteados por Hadamard es una piedra angular en la formulación matemática de fenómenos físicos, asegurando soluciones significativas y estables.
Hadamard fue un pionero en el desarrollo temprano del análisis funcional, un área que estudia espacios de funciones y operadores. Su libro "Leçons sur le calcul des variations", publicado en 1910, es considerado una obra fundacional. En ella, sistematizó y expandió el cálculo de variaciones, conectándolo con ideas emergentes en topología y análisis.
Su trabajo en esta área sentó las bases para desarrollos posteriores de figuras como Banach y Hilbert. Hadamard comprendió que muchos problemas de análisis clásico podían reformularse de manera más clara y poderosa dentro del contexto de espacios funcionales de dimensión infinita. Esta visión abstracta y unificadora es característica de su genio.
Por sus múltiples contribuciones, recibió premios de la más alta distinción, como el Premio Poncelet en 1898. Además, su liderazgo fue reconocido con la presidencia de la Sociedad Matemática de Francia en 1906 y una cátedra permanente en el prestigioso Collège de France.
Además de su producción puramente matemática, Hadamard dedicó una profunda reflexión al proceso mismo del descubrimiento. Su libro de 1945, "Psychology of Invention in the Mathematical Field", es un estudio seminal sobre la creatividad. En él, investigó los procesos mentales subyacentes a los momentos de insight y descubrimiento científico.
Hadamard basó su investigación en entrevistas personales con algunos de los grandes matemáticos y físicos de su tiempo, incluidos Henri Poincaré y Albert Einstein. A partir de estos testimonios, propuso un modelo de creatividad en dos etapas que sigue siendo relevante en la filosofía de la mente y la ciencia cognitiva actual.
Hadamard argumentó que el trabajo inconsciente es fundamental para la innovación. Su análisis conectaba la creatividad matemática con procesos psicológicos universales, desmitificando la idea del genio como un mero ejercicio de lógica fría y consciente.
Su modelo de dos etapas para la invención matemática ha influido en estudios modernos sobre libre albedrío, innovación y los procesos cerebrales detrás del pensamiento creativo.
El impacto del trabajo de Jacques Hadamard no se detuvo en el siglo XX. Por el contrario, sus conceptos y herramientas encuentran aplicaciones vibrantes en tecnologías de vanguardia como la computación cuántica y el procesamiento de señales. Esta capacidad de trascender su época es el sello de un verdadero visionario.
Quizás la aplicación más fascinante y contemporánea de su legado es la puerta de Hadamard en computación cuántica. Esta operación fundamental actúa sobre un qubit, la unidad básica de información cuántica. La puerta crea un estado de superposición, permitiendo al qubit estar simultáneamente en un estado |0⟩ y |1⟩ con igual probabilidad.
Esta transformación, inspirada directamente en las matrices de Hadamard, es la base de algoritmos cuánticos poderosos, como el algoritmo de búsqueda de Grover y el algoritmo de factorización de Shor. La conexión es profunda: la ortogonalidad y las propiedades espectrales de sus matrices del siglo XIX resultaron ser ideales para manipular la superposición cuántica.
En el ámbito de las comunicaciones y el procesamiento digital, las matrices de Hadamard son indispensables. Se utilizan en la construcción de códigos de corrección de errores, como los códigos de Reed-Muller, que protegen la integridad de los datos en transmisiones satelitales y almacenamiento digital. Su propiedad de ortogonalidad permite separar señales de manera eficiente.
En el procesamiento de imágenes y señales, la transformada de Walsh-Hadamard es una herramienta fundamental para la compresión y el análisis espectral. Es una versión más simple y computacionalmente eficiente que la transformada de Fourier, ampliamente utilizada en algoritmos de compresión de video y en procesamiento de señales de radar.
La versatilidad y utilidad práctica de un concepto matemático puro inventado por Hadamard es un testimonio de su profunda intuición. Sus ideas no solo resolvieron problemas abstractos, sino que también diseñaron, sin saberlo, las herramientas para tecnologías futuras.
Desde los satélites que orbitan la Tierra hasta los laboratorios de computación cuántica, el trabajo de Hadamard proporciona una infraestructura matemática crítica para la tecnología moderna.
Esta segunda parte del recorrido por la vida de Jacques Hadamard revela la asombrosa amplitud de su mente. Desde los fundamentos del análisis hasta los secretos de la creatividad y las aplicaciones tecnológicas más avanzadas, su legado es un monumento al pensamiento matemático puro y aplicado. Su figura se agiganta como la de un verdadero arquitecto del conocimiento científico del siglo XX y más allá.
La carrera de Jacques Hadamard se caracterizó por una productividad asombrosa y sostenida a lo largo de más de siete décadas. Sus períodos más intensos, como su estancia en Burdeos, fueron verdaderas tormentas de creatividad matemática. Los datos cuantitativos de su producción ofrecen una perspectiva clara de la magnitud de su genio y dedicación.
Entre los años 1893 y 1897, mientras ocupaba un puesto en Burdeos, Hadamard publicó la impresionante cantidad de 29 trabajos científicos profundos. Estos artículos no fueron meras notas triviales; abordaron temas fundamentales y variados, desde el análisis complejo hasta la teoría de números y las ecuaciones diferenciales. Esta etapa demostró su capacidad para trabajar en múltiples frentes con igual maestría.
A lo largo de su vida, su producción no decayó. Publicó cientos de artículos y varios libros fundamentales. Esta enorme productividad se explica no solo por su talento innato, sino también por su método riguroso y su habilidad para identificar problemas centrales en cada campo que tocaba. Su obra escrita es un mapa del pensamiento matemático avanzado de su época.
El reconocimiento a su trabajo llegó pronto y se mantuvo constante. Hadamard acumuló los más altos honores que el mundo académico francés e internacional podía otorgar. Estos premios no fueron solo distinciones personales, sino indicadores del valor transformador de sus contribuciones para las matemáticas como disciplina.
La trayectoria de premios de Hadamard —desde el Grand Prix hasta la silla en el Collège de France— es un testimonio del respeto unánime que inspiró entre sus contemporáneos.
Sus posiciones de liderazgo fueron igualmente destacadas. Suceder a Henri Poincaré, uno de los últimos polímatas universales, en la Academia de Ciencias en 1912, fue un reconocimiento simbólico de que él mismo ocupaba ese estatus. Como presidente de la Sociedad Matemática de Francia, guió la comunidad científica durante un período de gran fermentación intelectual.
La influencia de Jacques Hadamard no se ha desvanecido con el tiempo. Por el contrario, su legado se estudia, se analiza y se celebra en formatos modernos y accesibles. Su vida y obra continúan inspirando a nuevas generaciones de matemáticos, científicos e incluso público general interesado en la historia de las ideas.
El legado de este genio matemático ha encontrado un nuevo hogar en la era digital. En 2023, por ejemplo, se publicaron videos y podcasts educativos dedicados a desglosar su vida y sus contribuciones más importantes. Estos recursos hacen que su trabajo sea más accesible y demuestran el interés continuo en figuras que moldearon nuestra comprensión del mundo.
Biografías en línea, artículos de divulgación y entradas en enciclopedias digitales mantienen viva su memoria. Este fenómeno subraya una verdad fundamental: las contribuciones de Hadamard tienen una calidad atemporal. Sus definiciones, teoremas y marcos conceptuales son tan claros y potentes hoy como lo fueron hace un siglo.
La forma de hacer matemáticas de Hadamard, con su énfasis en el rigor, la generalidad y la claridad estructural, influyó profundamente en el nacimiento del influyente grupo Bourbaki en la década de 1930. Este colectivo de matemáticos franceses buscaba refundar las matemáticas sobre bases axiomáticas sólidas, un espíritu que resonaba con el trabajo sistematizador de Hadamard en análisis funcional.
Su idea de los problemas bien planteados se convirtió en un estándar en el análisis de ecuaciones diferenciales parciales, disciplina fundamental para la física teórica y la ingeniería. Su enfoque abstracto pero rigurosamente fundamentado ayudó a pivotar las matemáticas del siglo XX hacia una mayor abstracción, sin perder de vista las aplicaciones.
Al repasar la vida y obra de Jacques Hadamard, surge la imagen de un arquitecto intelectual de proporciones inigualables. Su genio no residió en un solo descubrimiento espectacular, sino en una serie de contribuciones fundamentales que redefinieron múltiples campos. Hadamard fue un puente entre el siglo XIX y el XX, entre la matemática clásica y la moderna, y entre la teoría pura y sus aplicaciones más insospechadas.
Podemos resumir su grandeza en varios pilares interconectados que explican por qué su legado es tan perdurable y respetado.
Jacques Hadamard encarnó la unión perfecta entre el pensador abstracto más puro y el arquitecto de herramientas que, en última instancia, modelan nuestro mundo tecnológico.
Finalmente, la figura de Hadamard trasciende el ámbito estricto de las matemáticas. Su activismo en el caso Dreyfus nos habla de un científico comprometido con la justicia y la verdad en el ámbito social. Su exilio durante la guerra refleja los trastornos del siglo XX que impactaron incluso a las mentes más brillantes. Y su libro sobre psicología de la invención lo conecta con las humanidades y las ciencias cognitivas.
Hoy, cuando un científico enuncia un problema bien planteado, cuando un ingeniero utiliza un código para proteger datos, o cuando un físico cuántico aplica una puerta de Hadamard a un qubit, están, conscientemente o no, caminando sobre los cimientos que este genio francés ayudó a construir. Jacques Hadamard no solo resolvió ecuaciones y demostró teoremas; dio forma a la forma misma en que pensamos sobre problemas complejos.
Su historia es un recordatorio poderoso de que la búsqueda más abstracta del conocimiento puro puede, con el tiempo, revelarse como la fuente más práctica para las revoluciones tecnológicas y conceptuales del futuro. Por eso, Jacques Hadamard sigue siendo, y seguirá siendo, un genio matemático de proporciones verdaderamente inigualables.



Your personal space to curate, organize, and share knowledge with the world.
Discover and contribute to detailed historical accounts and cultural stories. Share your knowledge and engage with enthusiasts worldwide.
Connect with others who share your interests. Create and participate in themed boards about any topic you have in mind.
Contribute your knowledge and insights. Create engaging content and participate in meaningful discussions across multiple languages.
Already have an account? Sign in here

Descubre cómo Henri Lebesgue revolucionó el análisis matemático con su integral, superando límites clásicos y sentando b...
View Board
Descubre el legado matemático de Émile Picard, visionario del siglo XIX. Explora sus teoremas, métodos y contribuciones ...
View Board
Explore the extraordinary legacy of Charles Hermite in modern mathematics through his pioneering contributions to number...
View Board
Explore the inspirational journey of Émile Picard, a pioneering French mathematician whose groundbreaking work in comple...
View Board
Descubre cómo Joseph Fourier revolucionó la ciencia con sus series matemáticas y la ecuación del calor, sentando las bas...
View Board
Explore the life and legacy of Jacques Hadamard, a pivotal mathematician of the 20th century whose innovations in number...
View Board
Descubre cómo Gastón Julia revolucionó las matemáticas con sus conjuntos fractales, sentando las bases de la geometría m...
View Board
Explore Charles Hermite's key math contributions: proving e's transcendence, Hermite polynomials, and shaping quantum me...
View Board
Discover the life and legacy of Gaston Julia, the brilliant mathematician who pioneered fractals and Julia sets, shaping...
View Board
Explore the life and groundbreaking innovations of Jean-Baptiste Joseph Fourier, the French mathematician and physicist ...
View Board
"Explore Jacques Hadamard's legacy: Prime Number Theorem proof, functional analysis, and impact on modern tech. Discover...
View Board
Discover the power of mathematical symbols and the visionaries behind them. Explore history, innovation, and the future ...
View Board
Entdecken Sie das Leben und Werk von Évariste Galois, dem mathematischen Genie, das die moderne Algebra revolutionierte....
View Board
Explore the remarkable legacy of Henri Cartan, the pioneering mathematician whose groundbreaking contributions to algebr...
View Board
Henri Lebesgue: The Mathematician Who Revolutionized Integration Henri Lebesgue was a French mathematician whose ground...
View Board
Discover how Pierre-Simon Laplace revolutionized science with his groundbreaking work in mathematics, astronomy, and pro...
View Board
Discover Euclid, the Father of Geometry, and his timeless work *Elements*. Explore his life, groundbreaking theorems, an...
View BoardÉmile Borel: A Pioneering Mathematician and Physicist The Early Life and Education of Émile Borel Émile Borel, born on...
View Board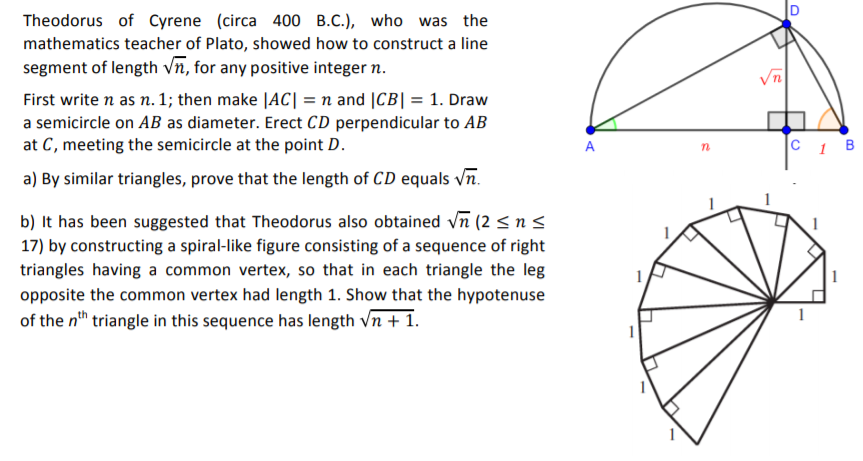
Theodorus of Cyrene, the ancient Greek mathematician and Plato's teacher, revolutionized geometry with his work on irrat...
View Board
Archimedes, the genius of ancient Greece, revolutionized mathematics, physics, and engineering with discoveries like pi,...
View Board
Comments