Explore Any Narratives
Discover and contribute to detailed historical accounts and cultural stories. Share your knowledge and engage with enthusiasts worldwide.
Jean-Baptiste Joseph Fourier fue un matemático y físico francés cuyo legado revolucionó la ciencia. Conocido como el maestro de las series matemáticas, su trabajo sentó las bases del análisis moderno de funciones y la física matemática. Sus ideas, como las series de Fourier y la ecuación del calor, siguen impulsando avances en ingeniería, procesamiento de señales y climatología.
Fourier calculó que la Tierra debería ser unos 32°C más fría sin un mecanismo atmosférico que retiene calor, un concepto pionero del efecto invernadero.
Su vida, marcada por la adversidad y el genio, transcurrió desde la Revolución Francesa hasta la Restauración. Fourier no solo teorizó; observó, experimentó y conectó matemáticas puras con fenómenos físicos tangibles. Este artículo explora su trayectoria, sus contribuciones fundamentales y su influencia perdurable en el mundo actual.
Joseph Fourier nació el 21 de marzo de 1768 en Auxerre, Francia. Fue el noveno hijo de un sastre y, tras quedar huérfano a una edad temprana, enfrentó una infancia difícil. Pese a estas circunstancias, su talento natural para las matemáticas se manifestó pronto y le abrió las puertas de su educación.
Recibió formación inicial en la escuela local, dirigida por maestros que reconocieron su potencial. Gracias a su brillantez, ingresó a la Escuela Militar de Auxerre y posteriormente a la prestigiosa École Normale Supérieure en París. Su carrera académica floreció en un contexto histórico turbulento, la Revolución Francesa, que influyó profundamente en su vida y oportunidades.
Su primera incursión en la enseñanza fue como profesor en la misma escuela militar donde estudió. Allí comenzó a desarrollar un interés profundo por la física matemática, particularmente por los problemas relacionados con la propagación del calor. Este interés marcaría el rumbo de sus investigaciones más famosas.
Una faceta menos conocida de Fourier fue su rol en la expedición de Napoleón a Egipto en 1798. Napoleón, reconociendo el valor de los intelectuales, reclutó a un grupo de científicos y eruditos. Fourier fue nombrado secretario del Instituto de Egipto, una institución fundada en El Cairo para estudiar la antigua y la nueva realidad egipcia.
Durante su estancia, Fourier participó activamente en exploraciones arqueológicas y en la administración del sistema educativo de la región. Contribuyó significativamente a la recopilación y estudio de antigüedades egipcias. Esta experiencia enriqueció su perspectiva científica, exponiéndolo a problemas de organización y observación a gran escala.
De regreso a Francia en 1801, llevó consigo no solo experiencia administrativa, sino también una profunda curiosidad por los fenómenos naturales. Fue nombrado prefecto del departamento de Isère, con sede en Grenoble, un puesto que ocupó hasta 1814. A pesar de sus deberes administrativos, fue en este periodo donde desarrolló su teoría analítica del calor.
La contribución más célebre de Fourier, presentada primero en 1807, es la ecuación del calor. Se trata de una ecuación diferencial parcial parabólica que describe matemáticamente cómo se difunde el calor en un sólido a lo largo del tiempo.
Su obra maestra, Théorie analytique de la chaleur (Teoría Analítica del Calor), publicada en 1822, sistematizó esta teoría. En ella, Fourier demostró que el flujo de calor es proporcional al gradiente de temperatura, un principio fundamental de la termodinámica. Su enfoque fue profundamente innovador al tratar el calor como una onda que podía descomponerse en componentes más simples.
La teoría no fue aceptada de inmediato. Matemáticos de la talla de Lagrange y Laplace cuestionaron su rigor, especialmente el uso de series infinitas para representar funciones arbitrarias, incluso discontinuas. Sin embargo, la potencia y utilidad práctica de su método eran innegables.
En 1811, Fourier presentó una versión revisada de su memoria a la Academia de Ciencias de París, la cual ganó el Gran Premio de la institución. Este reconocimiento, aunque no silenció todas las críticas, consolidó el valor de su trabajo. Las objeciones sobre el rigor fueron posteriormente abordadas y resueltas por matemáticos del siglo XIX como Dirichlet y Riemann.
Para resolver su ecuación del calor, Fourier desarrolló una herramienta matemática extraordinaria: las series de Fourier. Esta técnica permite descomponer cualquier función periódica, sin importar su complejidad, en una suma infinita de funciones seno y coseno simples, cada una con una amplitud y frecuencia específica.
Este método no solo resolvía la ecuación del calor, sino que abría una puerta a nuevas áreas de investigación. Fourier introdujo de manera implícita lo que hoy conocemos como la transformada de Fourier, aunque la formalización completa llegaría después. Su visión estableció un puente permanente entre el análisis matemático abstracto y las aplicaciones en ingeniería y física.
Las series de Fourier se convirtieron en la herramienta clave para resolver problemas de valores en la frontera. Estos problemas, que involucran ecuaciones diferenciales con condiciones específicas en los límites de un dominio, son ubicuos en la física. Desde el estudio de las vibraciones de una cuerda hasta el análisis de las manchas solares y las mareas, el método de Fourier ofrecía una solución sistemática y elegante.
Joseph Fourier no solo fue un genio matemático, sino también un visionario de la ciencia climática. En 1824, en sus escritos sobre las temperaturas terrestres, formuló una pregunta fundamental. Se preguntó por qué la Tierra era tan cálida y propuso la existencia de un mecanismo atmosférico que atrapa el calor, un concepto seminal del efecto invernadero.
Fourier realizó cálculos simples pero profundos sobre el balance energético del planeta. Comparó la energía recibida del Sol con la que la Tierra irradia de vuelta al espacio. Sus cálculos indicaban que, teóricamente, nuestro planeta debería ser mucho más frío de lo que es.
Fourier estimó una diferencia térmica de aproximadamente 32°C, calculando una temperatura superficial promedio esperada de -16°C, frente a los +16°C observados en la realidad. Esta discrepancia solo podía explicarse por la atmósfera.
Identificó que la atmósfera actúa como una barrera parcialmente transparente. Deja pasar la radiación solar de onda corta, pero es más opaca a la radiación infrarroja de onda larga que emite la superficie terrestre caliente. Aunque no conocía los gases específicos responsables, sugirió correctamente que el vapor de agua era un componente clave en este proceso de retención de calor.
Esta perspicaz intuición, publicada entre 1824 y 1827, sentó las bases conceptuales para la climatología moderna. Fourier puso el foco en la interacción entre energía y atmósfera, un principio central en los modelos climáticos actuales. Su trabajo es un testimonio temprano del poder de la física matemática para explicar fenómenos globales complejos.
El impacto más tangible y extendido del trabajo de Fourier se observa en el procesamiento digital de señales. La transformada de Fourier, derivada de sus series, es el algoritmo fundamental que permite analizar las componentes de frecuencia de cualquier señal.
Esta herramienta convierte una señal del dominio del tiempo (cómo varía en cada instante) al dominio de la frecuencia (qué tonos o frecuencias la componen). Esta conversión es la piedra angular de innumerables tecnologías de la era digital. Se estima que más del 90% de los algoritmos en procesamiento de señales se basan directa o indirectamente en los principios de Fourier.
Las aplicaciones de la transformada de Fourier son omnipresentes en nuestra vida diaria. Sin ellas, las comunicaciones modernas y el entretenimiento digital no existirían en su forma actual.
Los métodos de Fourier trascendieron la teoría del calor para infiltrarse en prácticamente todas las ramas de la física y la ingeniería. Su enfoque de descomponer problemas complejos en oscillaciones simples demostró ser universalmente poderoso.
En áreas como la acústica, la óptica y la mecánica cuántica, las series y transformadas de Fourier son herramientas de análisis indispensables. Permiten estudiar patrones de difracción de la luz, las vibraciones en estructuras, y las funciones de onda de las partículas subatómicas. Este enfoque unificador es un sello distintivo de su legado.
La revolución digital se aceleró con el desarrollo del algoritmo de la Transformada Rápida de Fourier (FFT) en 1965. Este algoritmo hizo computacionalmente viable aplicar la transformada de Fourier a señales digitales en tiempo real.
La magnitud de la contribución de Fourier fue celebrada oficialmente dos siglos después de sus descubrimientos más importantes. En 2018, la Sociedad Matemática Francesa, en colaboración con otras instituciones, declaró el "Año Nacional Fourier".
Este homenaje extendido tuvo como objetivo destacar la profunda y continua influencia de su trabajo en la ciencia moderna. Se organizaron conferencias, exposiciones y publicaciones especiales en toda Francia, dirigidas tanto a la comunidad académica como al público general. El evento consolidó a Fourier no solo como una figura histórica, sino como un pilar de la ciencia contemporánea.
El camino hacia la aceptación total de las ideas de Fourier dentro de las matemáticas puras fue riguroso. Las críticas iniciales de Lagrange y otros sobre la convergencia de las series para funciones discontinuas señalaban un vacío de rigor. Este vacío, sin embargo, impulsó décadas de investigación fructífera.
Matemáticos del más alto nivel dedicaron sus esfuerzos a formalizar y generalizar las intuiciones de Fourier. Este proceso de rigorización fue esencial para el avance del análisis matemático en el siglo XIX y más allá.
Este proceso demuestra cómo una idea física potente y útil puede impulsar el desarrollo de matemáticas abstractas de primer nivel, creando un ciclo virtuoso entre teoría y aplicación.
El pensamiento de Joseph Fourier encuentra nuevas y sorprendentes aplicaciones en las fronteras tecnológicas del siglo XXI. Su legado no es un relicario del pasado, sino un conjunto de herramientas activas que impulsan la innovación. En campos como la inteligencia artificial y la modelación climática, sus principios matemáticos son más relevantes que nunca.
En el ámbito del aprendizaje automático y el análisis de datos, las transformadas de Fourier son cruciales para el procesamiento de señales y el análisis espectral. Los algoritmos de IA utilizan estas técnicas para preprocesar datos de audio, imágenes y series temporales, extrayendo características fundamentales que mejoran la precisión de los modelos. Este es un ejemplo perfecto de cómo las matemáticas del siglo XIX alimentan la revolución digital actual.
Los modelos climáticos globales, esenciales para entender el cambio climático y proyectar escenarios futuros, dependen en gran medida de métodos espectrales derivados del trabajo de Fourier. Estos métodos permiten resolver eficientemente las complejas ecuaciones diferenciales que describen la dinámica de la atmósfera y los océanos.
Su pionera conceptualización del efecto invernadero es el punto de partida teórico para toda la ciencia del clima. Los científicos hoy cuantifican el forzamiento radiativo de gases como el CO2 utilizando un marco conceptual que Fourier vislumbró hace 200 años. Su legado, por tanto, es central en los esfuerzos globales por la sostenibilidad y la comprensión de nuestro impacto en el planeta.
Más allá de sus fórmulas y teoremas, la mayor contribución de Fourier puede ser su enfoque filosófico hacia la ciencia. En una época dominada por el racionalismo puro, él defendió y practicó la primacía de la observación y el experimento. Creía que las matemáticas debían surgir del estudio de los fenómenos naturales, no al revés.
Esta postura lo enfrentó a contemporáneos más teóricos, pero también lo convirtió en un puente fundamental. Su trabajo demuestra que los avances más profundos a menudo ocurren en la intersección entre matemáticas puras y física aplicada. Su carrera, que abarcó desde la administración en Egipto hasta la termodinámica y el análisis matemático, es un testimonio del pensamiento interdisciplinario.
"El estudio profundo de la naturaleza es la fuente más fértil de descubrimientos matemáticos." - Esta frase, atribuida al espíritu de su trabajo, encapsula su creencia en una ciencia fundamentada en la observación del mundo real.
En 1822, Fourier fue elegido Secretario Perpetuo de la Académie des Sciences de París. Este prestigioso cargo le permitió influir en la dirección de la ciencia francesa y europea de la época. Utilizó esta plataforma para promover no solo sus propias ideas, sino también el trabajo de otros científicos y la importancia de la investigación experimental.
Su participación en la expedición a Egipto y su labor en el Instituto de Egipto también reflejan su visión de la ciencia como una empresa cultural y humanística amplia. Fourier entendía que el conocimiento matemático y la exploración geográfica y arqueológica eran partes de un mismo impulso por comprender el mundo en su totalidad.
Al revisar la vida y obra de Jean-Baptiste Joseph Fourier, es imposible no maravillarse ante la amplitud y profundidad de su impacto. De un origen humilde y una infancia difícil, se elevó a través del intelecto puro para convertirse en un arquitecto de conceptos que definen nuestra comprensión moderna del universo físico y digital.
Su historia es la de un visionario cuyas ideas, inicialmente cuestionadas, se convirtieron en los cimientos de múltiples disciplinas científicas y tecnológicas. Fourier nos enseñó que a veces, la herramienta matemática más poderosa es una nueva forma de ver y descomponer un problema.
Para consolidar su extraordinario legado, podemos enumerar sus aportes fundamentales que resuenan hasta hoy:
Joseph Fourier falleció en París el 16 de mayo de 1830, pero su espíritu de investigación y su obra monumental están más vivos que nunca. Cada vez que un archivo de música se comprime en formato MP3, una imagen médica se reconstruye en una resonancia magnética, o un modelo climático simula el futuro de nuestro planeta, estamos utilizando extensiones directas de su genio.
Su legado es un recordatorio poderoso de que las contribuciones científicas más trascendentales a menudo son aquellas que proporcionan un nuevo lenguaje o una nueva lente para observar la realidad. Fourier nos dio ambas cosas: un lenguaje matemático para describir cualquier oscilación y una lente para ver el calor, las ondas y las señales de una manera completamente nueva.
Desde las aplicaciones más prácticas en nuestros teléfonos inteligentes hasta las especulaciones más abstractas en física teórica, el trabajo de Fourier sigue siendo un pilar indispensable. Su historia nos inspira a valorar la curiosidad interdisciplinaria, a perseverar frente al escepticismo y a confiar en que las matemáticas, cuando se nutren de los problemas del mundo real, pueden revelar una belleza y una utilidad inagotables. El maestro de las series matemáticas, en efecto, sigue transformando la ciencia y, con ella, nuestro mundo.



Your personal space to curate, organize, and share knowledge with the world.
Discover and contribute to detailed historical accounts and cultural stories. Share your knowledge and engage with enthusiasts worldwide.
Connect with others who share your interests. Create and participate in themed boards about any topic you have in mind.
Contribute your knowledge and insights. Create engaging content and participate in meaningful discussions across multiple languages.
Already have an account? Sign in here

Descubre cómo Henri Lebesgue revolucionó el análisis matemático con su integral, superando límites clásicos y sentando b...
View Board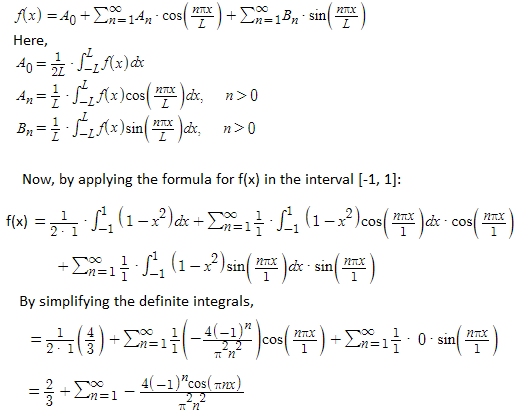
Explore the life and groundbreaking innovations of Jean-Baptiste Joseph Fourier, the French mathematician and physicist ...
View Board
Descubre la vida y legado de Jacques Hadamard, el genio matemático francés que revolucionó el análisis matemático, demos...
View Board
Explore the inspirational journey of Émile Picard, a pioneering French mathematician whose groundbreaking work in comple...
View Board
Descubre el legado matemático de Émile Picard, visionario del siglo XIX. Explora sus teoremas, métodos y contribuciones ...
View BoardÉmile Borel: A Pioneering Mathematician and Physicist The Early Life and Education of Émile Borel Émile Borel, born on...
View Board
Discover how Pierre-Simon Laplace revolutionized science with his groundbreaking work in mathematics, astronomy, and pro...
View Board
Discover the groundbreaking legacy of Louis de Broglie, the pioneering scientist behind wave-particle duality. This insi...
View Board
Explore Roger Penrose's groundbreaking contributions to physics, black holes, quantum consciousness, and aperiodic tilin...
View Board
Louis Néel Nobel laureate revolutionized magnetism research with discovery of antiferromagnetism advancing condensed mat...
View Board
André-Marie Ampère: A Pioneer in the History of Electricity The Early Life and Education André-Marie Ampère, often rega...
View Board
Erwin Schrödinger's groundbreaking work in quantum mechanics, his famous thought experiment Schrödinger's cat, and his c...
View Board
Descubre cómo Carl Wieman, premio Nobel de Física, revolucionó la educación científica. De atrapar átomos a transformar ...
View Board
Henri Lebesgue: The Mathematician Who Revolutionized Integration Henri Lebesgue was a French mathematician whose ground...
View Board
James Clerk Maxwell unified electricity and magnetism into a single mathematical framework, his work laying the foundati...
View Board
Discover the enduring legacy of Léon Brillouin, a 20th-century visionary physicist who bridged theoretical and applied s...
View Board
"Explore Henri Poincaré's groundbreaking work in math, physics, and philosophy, shaping modern science through chaos the...
View Board
Explore the life and legacy of Evangelista Torricelli, the 17th-century Italian physicist whose invention of the baromet...
View Board
Max Born was a renowned theoretical physicist and Nobel laureate known for his statistical interpretation of quantum mec...
View Board
Discover Alan Turing's groundbreaking contributions to computing, AI, and WWII codebreaking. Explore his legacy and endu...
View Board
Comments