Joseph Fourier: El Maestro de las Series Matemáticas
Jean-Baptiste Joseph Fourier fue un matemático y físico francés cuyo legado revolucionó la ciencia. Conocido como el maestro de las series matemáticas, su trabajo sentó las bases del análisis moderno de funciones y la física matemática. Sus ideas, como las series de Fourier y la ecuación del calor, siguen impulsando avances en ingeniería, procesamiento de señales y climatología.
Fourier calculó que la Tierra debería ser unos 32°C más fría sin un mecanismo atmosférico que retiene calor, un concepto pionero del efecto invernadero.
Su vida, marcada por la adversidad y el genio, transcurrió desde la Revolución Francesa hasta la Restauración. Fourier no solo teorizó; observó, experimentó y conectó matemáticas puras con fenómenos físicos tangibles. Este artículo explora su trayectoria, sus contribuciones fundamentales y su influencia perdurable en el mundo actual.
De Auxerre a París: Una Vida de Superación
Joseph Fourier nació el 21 de marzo de 1768 en Auxerre, Francia. Fue el noveno hijo de un sastre y, tras quedar huérfano a una edad temprana, enfrentó una infancia difícil. Pese a estas circunstancias, su talento natural para las matemáticas se manifestó pronto y le abrió las puertas de su educación.
Formación y Primeros Años
Recibió formación inicial en la escuela local, dirigida por maestros que reconocieron su potencial. Gracias a su brillantez, ingresó a la Escuela Militar de Auxerre y posteriormente a la prestigiosa École Normale Supérieure en París. Su carrera académica floreció en un contexto histórico turbulento, la Revolución Francesa, que influyó profundamente en su vida y oportunidades.
Su primera incursión en la enseñanza fue como profesor en la misma escuela militar donde estudió. Allí comenzó a desarrollar un interés profundo por la física matemática, particularmente por los problemas relacionados con la propagación del calor. Este interés marcaría el rumbo de sus investigaciones más famosas.
La Expedición a Egipto: Un Matemático como Administrador
Una faceta menos conocida de Fourier fue su rol en la expedición de Napoleón a Egipto en 1798. Napoleón, reconociendo el valor de los intelectuales, reclutó a un grupo de científicos y eruditos. Fourier fue nombrado secretario del Instituto de Egipto, una institución fundada en El Cairo para estudiar la antigua y la nueva realidad egipcia.
Contribuciones a la Egiptología
Durante su estancia, Fourier participó activamente en exploraciones arqueológicas y en la administración del sistema educativo de la región. Contribuyó significativamente a la recopilación y estudio de antigüedades egipcias. Esta experiencia enriqueció su perspectiva científica, exponiéndolo a problemas de organización y observación a gran escala.
De regreso a Francia en 1801, llevó consigo no solo experiencia administrativa, sino también una profunda curiosidad por los fenómenos naturales. Fue nombrado prefecto del departamento de Isère, con sede en Grenoble, un puesto que ocupó hasta 1814. A pesar de sus deberes administrativos, fue en este periodo donde desarrolló su teoría analítica del calor.
La Ecuación del Calor: Un Pilar de la Física Matemática
La contribución más célebre de Fourier, presentada primero en 1807, es la ecuación del calor. Se trata de una ecuación diferencial parcial parabólica que describe matemáticamente cómo se difunde el calor en un sólido a lo largo del tiempo.
Su obra maestra, Théorie analytique de la chaleur (Teoría Analítica del Calor), publicada en 1822, sistematizó esta teoría. En ella, Fourier demostró que el flujo de calor es proporcional al gradiente de temperatura, un principio fundamental de la termodinámica. Su enfoque fue profundamente innovador al tratar el calor como una onda que podía descomponerse en componentes más simples.
Recepción y Críticas Iniciales
La teoría no fue aceptada de inmediato. Matemáticos de la talla de Lagrange y Laplace cuestionaron su rigor, especialmente el uso de series infinitas para representar funciones arbitrarias, incluso discontinuas. Sin embargo, la potencia y utilidad práctica de su método eran innegables.
En 1811, Fourier presentó una versión revisada de su memoria a la Academia de Ciencias de París, la cual ganó el Gran Premio de la institución. Este reconocimiento, aunque no silenció todas las críticas, consolidó el valor de su trabajo. Las objeciones sobre el rigor fueron posteriormente abordadas y resueltas por matemáticos del siglo XIX como Dirichlet y Riemann.
El Nacimiento de las Series de Fourier
Para resolver su ecuación del calor, Fourier desarrolló una herramienta matemática extraordinaria: las series de Fourier. Esta técnica permite descomponer cualquier función periódica, sin importar su complejidad, en una suma infinita de funciones seno y coseno simples, cada una con una amplitud y frecuencia específica.
- Revolución Analítica: Proporcionó un nuevo lenguaje para analizar funciones complejas y fenómenos ondulatorios.
- Abstracción Poderosa: Transformó problemas físicos intrincados en problemas algebraicos más manejables.
- Fundamento Teórico: Sentó las bases para el desarrollo posterior del análisis de funciones de variable real y la teoría de integración.
Este método no solo resolvía la ecuación del calor, sino que abría una puerta a nuevas áreas de investigación. Fourier introdujo de manera implícita lo que hoy conocemos como la transformada de Fourier, aunque la formalización completa llegaría después. Su visión estableció un puente permanente entre el análisis matemático abstracto y las aplicaciones en ingeniería y física.
Impacto en la Resolución de Problemas de Frontera
Las series de Fourier se convirtieron en la herramienta clave para resolver problemas de valores en la frontera. Estos problemas, que involucran ecuaciones diferenciales con condiciones específicas en los límites de un dominio, son ubicuos en la física. Desde el estudio de las vibraciones de una cuerda hasta el análisis de las manchas solares y las mareas, el método de Fourier ofrecía una solución sistemática y elegante.
La Ciencia del Efecto Invernadero: Una Visión Precursora
Joseph Fourier no solo fue un genio matemático, sino también un visionario de la ciencia climática. En 1824, en sus escritos sobre las temperaturas terrestres, formuló una pregunta fundamental. Se preguntó por qué la Tierra era tan cálida y propuso la existencia de un mecanismo atmosférico que atrapa el calor, un concepto seminal del efecto invernadero.
Fourier realizó cálculos simples pero profundos sobre el balance energético del planeta. Comparó la energía recibida del Sol con la que la Tierra irradia de vuelta al espacio. Sus cálculos indicaban que, teóricamente, nuestro planeta debería ser mucho más frío de lo que es.
Fourier estimó una diferencia térmica de aproximadamente 32°C, calculando una temperatura superficial promedio esperada de -16°C, frente a los +16°C observados en la realidad. Esta discrepancia solo podía explicarse por la atmósfera.
El Rol de la Atmósfera como Aislante
Identificó que la atmósfera actúa como una barrera parcialmente transparente. Deja pasar la radiación solar de onda corta, pero es más opaca a la radiación infrarroja de onda larga que emite la superficie terrestre caliente. Aunque no conocía los gases específicos responsables, sugirió correctamente que el vapor de agua era un componente clave en este proceso de retención de calor.
Esta perspicaz intuición, publicada entre 1824 y 1827, sentó las bases conceptuales para la climatología moderna. Fourier puso el foco en la interacción entre energía y atmósfera, un principio central en los modelos climáticos actuales. Su trabajo es un testimonio temprano del poder de la física matemática para explicar fenómenos globales complejos.
El Legado en el Procesamiento de Señales Moderno
El impacto más tangible y extendido del trabajo de Fourier se observa en el procesamiento digital de señales. La transformada de Fourier, derivada de sus series, es el algoritmo fundamental que permite analizar las componentes de frecuencia de cualquier señal.
Esta herramienta convierte una señal del dominio del tiempo (cómo varía en cada instante) al dominio de la frecuencia (qué tonos o frecuencias la componen). Esta conversión es la piedra angular de innumerables tecnologías de la era digital. Se estima que más del 90% de los algoritmos en procesamiento de señales se basan directa o indirectamente en los principios de Fourier.
Aplicaciones Ubicuas en la Tecnología Actual
Las aplicaciones de la transformada de Fourier son omnipresentes en nuestra vida diaria. Sin ellas, las comunicaciones modernas y el entretenimiento digital no existirían en su forma actual.
- Compresión de Audio y Imagen: Formatos como MP3 y JPEG utilizan la transformada para eliminar componentes de frecuencia inaudibles o detalles visuales imperceptibles, reduciendo drásticamente el tamaño de los archivos.
- Comunicaciones Inalámbricas: Es esencial en tecnologías como WiFi, 4G/5G, y GPS para modular, transmitir y filtrar señales de radio de manera eficiente y libre de interferencias.
- Análisis Médico: Las máquinas de Resonancia Magnética (MRI) y los ecógrafos utilizan transformadas de Fourier para reconstruir imágenes precisas del interior del cuerpo humano a partir de datos de señales crudas.
- Reconocimiento de Voz y Análisis Musical: Permite a los software identificar palabras o analizar la estructura armónica de una canción descomponiendo la señal de audio en sus frecuencias constitutivas.
Influencia en la Física y la Ingeniería Contemporáneas
Los métodos de Fourier trascendieron la teoría del calor para infiltrarse en prácticamente todas las ramas de la física y la ingeniería. Su enfoque de descomponer problemas complejos en oscillaciones simples demostró ser universalmente poderoso.
En áreas como la acústica, la óptica y la mecánica cuántica, las series y transformadas de Fourier son herramientas de análisis indispensables. Permiten estudiar patrones de difracción de la luz, las vibraciones en estructuras, y las funciones de onda de las partículas subatómicas. Este enfoque unificador es un sello distintivo de su legado.
El Poder de la Transformada Rápida de Fourier (FFT)
La revolución digital se aceleró con el desarrollo del algoritmo de la Transformada Rápida de Fourier (FFT) en 1965. Este algoritmo hizo computacionalmente viable aplicar la transformada de Fourier a señales digitales en tiempo real.
- Aceleración Exponencial: La FFT redujo la complejidad computacional de N² operaciones a N·log(N), un avance monumental.
- Procesamiento en Tiempo Real: Habilitó aplicaciones como el radar moderno, el análisis espectral instantáneo y los efectos de sonido digital.
- Simulaciones Computacionales: Es la base de software de simulación como COMSOL Multiphysics, utilizado para resolver ecuaciones diferenciales en modelos complejos de ingeniería.
Un Reconocimiento Póstumo: El Año Nacional Fourier
La magnitud de la contribución de Fourier fue celebrada oficialmente dos siglos después de sus descubrimientos más importantes. En 2018, la Sociedad Matemática Francesa, en colaboración con otras instituciones, declaró el "Año Nacional Fourier".
Este homenaje extendido tuvo como objetivo destacar la profunda y continua influencia de su trabajo en la ciencia moderna. Se organizaron conferencias, exposiciones y publicaciones especiales en toda Francia, dirigidas tanto a la comunidad académica como al público general. El evento consolidó a Fourier no solo como una figura histórica, sino como un pilar de la ciencia contemporánea.
Críticas y Consolidación del Legado Matemático
El camino hacia la aceptación total de las ideas de Fourier dentro de las matemáticas puras fue riguroso. Las críticas iniciales de Lagrange y otros sobre la convergencia de las series para funciones discontinuas señalaban un vacío de rigor. Este vacío, sin embargo, impulsó décadas de investigación fructífera.
Matemáticos del más alto nivel dedicaron sus esfuerzos a formalizar y generalizar las intuiciones de Fourier. Este proceso de rigorización fue esencial para el avance del análisis matemático en el siglo XIX y más allá.
- Peter Gustav Lejeune Dirichlet (1829): Estableció las primeras condiciones suficientes rigurosas para la convergencia de las series de Fourier.
- Bernhard Riemann: Desarrolló su teoría de la integración, en parte motivado por el estudio de estas series, ampliando el conjunto de funciones que podían representarse.
- Henri Lebesgue (1902): Con su integral, proporcionó el marco más general y poderoso para el análisis de Fourier, cerrando el ciclo de rigorización iniciado con las dudas un siglo antes.
Este proceso demuestra cómo una idea física potente y útil puede impulsar el desarrollo de matemáticas abstractas de primer nivel, creando un ciclo virtuoso entre teoría y aplicación.
Fourier en el Siglo XXI: IA, Clima y Más Allá
El pensamiento de Joseph Fourier encuentra nuevas y sorprendentes aplicaciones en las fronteras tecnológicas del siglo XXI. Su legado no es un relicario del pasado, sino un conjunto de herramientas activas que impulsan la innovación. En campos como la inteligencia artificial y la modelación climática, sus principios matemáticos son más relevantes que nunca.
En el ámbito del aprendizaje automático y el análisis de datos, las transformadas de Fourier son cruciales para el procesamiento de señales y el análisis espectral. Los algoritmos de IA utilizan estas técnicas para preprocesar datos de audio, imágenes y series temporales, extrayendo características fundamentales que mejoran la precisión de los modelos. Este es un ejemplo perfecto de cómo las matemáticas del siglo XIX alimentan la revolución digital actual.
Modelación Climática y Sostenibilidad
Los modelos climáticos globales, esenciales para entender el cambio climático y proyectar escenarios futuros, dependen en gran medida de métodos espectrales derivados del trabajo de Fourier. Estos métodos permiten resolver eficientemente las complejas ecuaciones diferenciales que describen la dinámica de la atmósfera y los océanos.
Su pionera conceptualización del efecto invernadero es el punto de partida teórico para toda la ciencia del clima. Los científicos hoy cuantifican el forzamiento radiativo de gases como el CO2 utilizando un marco conceptual que Fourier vislumbró hace 200 años. Su legado, por tanto, es central en los esfuerzos globales por la sostenibilidad y la comprensión de nuestro impacto en el planeta.
La Filosofía Científica de Fourier: Un Puente entre Disciplinas
Más allá de sus fórmulas y teoremas, la mayor contribución de Fourier puede ser su enfoque filosófico hacia la ciencia. En una época dominada por el racionalismo puro, él defendió y practicó la primacía de la observación y el experimento. Creía que las matemáticas debían surgir del estudio de los fenómenos naturales, no al revés.
Esta postura lo enfrentó a contemporáneos más teóricos, pero también lo convirtió en un puente fundamental. Su trabajo demuestra que los avances más profundos a menudo ocurren en la intersección entre matemáticas puras y física aplicada. Su carrera, que abarcó desde la administración en Egipto hasta la termodinámica y el análisis matemático, es un testimonio del pensamiento interdisciplinario.
"El estudio profundo de la naturaleza es la fuente más fértil de descubrimientos matemáticos." - Esta frase, atribuida al espíritu de su trabajo, encapsula su creencia en una ciencia fundamentada en la observación del mundo real.
Secretario Perpetuo y Difusor de la Ciencia
En 1822, Fourier fue elegido Secretario Perpetuo de la Académie des Sciences de París. Este prestigioso cargo le permitió influir en la dirección de la ciencia francesa y europea de la época. Utilizó esta plataforma para promover no solo sus propias ideas, sino también el trabajo de otros científicos y la importancia de la investigación experimental.
Su participación en la expedición a Egipto y su labor en el Instituto de Egipto también reflejan su visión de la ciencia como una empresa cultural y humanística amplia. Fourier entendía que el conocimiento matemático y la exploración geográfica y arqueológica eran partes de un mismo impulso por comprender el mundo en su totalidad.
Reflexiones Finales: El Legado Inmortal de un Maestro
Al revisar la vida y obra de Jean-Baptiste Joseph Fourier, es imposible no maravillarse ante la amplitud y profundidad de su impacto. De un origen humilde y una infancia difícil, se elevó a través del intelecto puro para convertirse en un arquitecto de conceptos que definen nuestra comprensión moderna del universo físico y digital.
Su historia es la de un visionario cuyas ideas, inicialmente cuestionadas, se convirtieron en los cimientos de múltiples disciplinas científicas y tecnológicas. Fourier nos enseñó que a veces, la herramienta matemática más poderosa es una nueva forma de ver y descomponer un problema.
Resumen de las Contribuciones Clave
Para consolidar su extraordinario legado, podemos enumerar sus aportes fundamentales que resuenan hasta hoy:
- Las Series de Fourier: Una técnica revolucionaria para descomponer funciones complejas en oscilaciones simples, transformando el análisis matemático y la física.
- La Ecuación del Calor: La primera ecuación diferencial parcial parabólica resuelta sistemáticamente, sentando las bases de la teoría matemática de la difusión y la termodinámica.
- El Concepto del Efecto Invernadero: Una explicación física pionera para la temperatura terrestre, sentando las bases conceptuales de la climatología moderna.
- La Transformada de Fourier (implícita): El principio fundamental detrás del análisis espectral, que impulsa el procesamiento digital de señales, las comunicaciones y la imagen médica.
- Un Enfoque Científico Holístico: Una filosofía que priorizaba la observación y la aplicación, construyendo un puente duradero entre la teoría matemática abstracta y los fenómenos físicos del mundo real.
Conclusión: Un Eco que Perdura en Cada Frecuencia
Joseph Fourier falleció en París el 16 de mayo de 1830, pero su espíritu de investigación y su obra monumental están más vivos que nunca. Cada vez que un archivo de música se comprime en formato MP3, una imagen médica se reconstruye en una resonancia magnética, o un modelo climático simula el futuro de nuestro planeta, estamos utilizando extensiones directas de su genio.
Su legado es un recordatorio poderoso de que las contribuciones científicas más trascendentales a menudo son aquellas que proporcionan un nuevo lenguaje o una nueva lente para observar la realidad. Fourier nos dio ambas cosas: un lenguaje matemático para describir cualquier oscilación y una lente para ver el calor, las ondas y las señales de una manera completamente nueva.
Desde las aplicaciones más prácticas en nuestros teléfonos inteligentes hasta las especulaciones más abstractas en física teórica, el trabajo de Fourier sigue siendo un pilar indispensable. Su historia nos inspira a valorar la curiosidad interdisciplinaria, a perseverar frente al escepticismo y a confiar en que las matemáticas, cuando se nutren de los problemas del mundo real, pueden revelar una belleza y una utilidad inagotables. El maestro de las series matemáticas, en efecto, sigue transformando la ciencia y, con ella, nuestro mundo.
Émile Picard: Visionario Matemático del Siglo XIX
El matemático francés Charles-Émile Picard es una figura monumental de la ciencia del siglo XIX. Sus contribuciones, que abarcan desde el análisis complejo hasta la geometría algebraica, no solo definieron campos enteros sino que sentaron las bases para el desarrollo matemático moderno. Este artículo explora la vida y el legado imperecedero de un verdadero visionario.
Vida y Formación de un Genio Matemático
Charles-Émile Picard nació el 24 de julio de 1856 en París, en el seno de una familia de clase media. Su precoz talento para las matemáticas se manifestó desde muy joven. Tras una educación destacada, ingresó en la prestigiosa École Normale Supérieure en 1874, donde estudió bajo la influencia de grandes matemáticos de la época.
Su ascenso académico fue meteórico. A los 22 años obtuvo su doctorado y, pocos años después, en 1879, fue nombrado profesor en la Universidad de Toulouse. Esta posición fue solo el inicio de una carrera académica que lo llevaría a las instituciones más importantes de Francia, consolidando su reputación como uno de los matemáticos más influyentes de su generación.
Una Carrera Académica Distinguida
La trayectoria de Picard es una crónica de reconocimientos y responsabilidades crecientes. En 1898, regresó a París para ocupar una cátedra en la Sorbona y en la École Normale Supérieure. Su influencia se extendió más allá de las aulas cuando, en 1917, fue elegido secretario permanente de la Academia de Ciencias de Francia, un puesto de enorme prestigio que ocupó hasta su muerte.
Picard fue también un prolífico autor de textos académicos y un biógrafo dedicado de sus colegas matemáticos. Su obra escrita, tanto técnica como histórica, refleja una mente profundamente erudita y comprometida con la difusión del conocimiento científico.
Contribuciones Fundamentales al Análisis Complejo
Sin duda, el área donde Picard dejó una huella más profunda fue en la teoría de funciones de variable compleja. Sus célebres teoremas de Picard representan un salto conceptual que sigue siendo enseñado y aplicado en todo el mundo.
Estos teoremas, publicados en 1879, responden preguntas fundamentales sobre el comportamiento de las funciones analíticas. Su belleza reside en la contundencia y generalidad de sus conclusiones, que revelan propiedades universales de estas funciones.
El Teorema Pequeño de Picard
Este teorema establece una propiedad sorprendente sobre las funciones enteras, es decir, aquellas funciones que son analíticas en todo el plano complejo. Afirma que una función entera no constante toma todos los valores complejos posibles, con la excepción de, como máximo, un valor.
Por ejemplo, la función exponencial *ez* nunca toma el valor cero, pero sí toma cualquier otro valor complejo infinitas veces. Este resultado demostró que el comportamiento de las funciones enteras está extremadamente restringido y abrió nuevas vías de investigación en análisis.
El Teorema Grande de Picard
El teorema grande extiende esta idea a las singularidades esenciales, que son puntos donde una función tiene un comportamiento particularmente salvaje. Picard demostró que en cualquier vecindad de una singularidad esencial, la función toma todos los valores complejos infinitas veces, nuevamente con la posible excepción de un solo valor.
Los teoremas de Picard revolucionaron la comprensión de las funciones complejas y se convirtieron en piedras angulares de la teoría. Su impacto perdura en la investigación contemporánea en análisis y topología.
Estos resultados no fueron solo un triunfo teórico. Proporcionaron herramientas poderosas para el estudio de ecuaciones diferenciales y la geometría de superficies, conectando elegantemente distintas áreas de las matemáticas. Su influencia es tal que hoy se estudian en todos los cursos avanzados de análisis complejo.
El Método de Picard en Ecuaciones Diferenciales
Otra contribución monumental de Picard fue en el campo de las ecuaciones diferenciales. Desarrolló un procedimiento iterativo para demostrar la existencia y unicidad de soluciones, conocido universalmente como el método de aproximaciones sucesivas de Picard o simplemente iteración de Picard.
Este método aborda el llamado problema de Cauchy, que busca una función que satisfaga una ecuación diferencial dada junto con una condición inicial específica. Picard ideó una forma constructiva de generar una sucesión de funciones que, bajo ciertas condiciones, converge a la solución exacta.
Aplicaciones y Legado del Método
La importancia práctica del método de Picard es inmensa. Proporciona no solo una prueba de existencia, sino también un algoritmo numérico para aproximar soluciones. Hoy, este algoritmo está implementado en software matemático como MATLAB y se enseña en cursos de ecuaciones diferenciales y análisis numérico en todo el mundo.
- Demostración Constructiva: A diferencia de otros teoremas de existencia, el método de Picard muestra explícitamente cómo construir la solución.
- Base para Generalizaciones: Sus ideas fueron extendidas a ecuaciones diferenciales parciales y a sistemas más complejos, dando origen a la teoría Picard-Vessiot.
- Puente entre Teoría y Cálculo: Este método conecta el mundo abstracto de la existencia de soluciones con el mundo concreto de su cálculo aproximado.
Además, Picard aplicó sus técnicas al estudio de ecuaciones diferenciales lineales, investigando sus grupos de transformaciones. Este trabajo fue fundamental en el desarrollo de la teoría de Galois para ecuaciones diferenciales, un área de investigación activa en el álgebra moderna.
Reconocimientos y Premios Internacionales
A lo largo de su vida, Émile Picard recibió numerosos honores que reflejaban la alta estima en que la comunidad científica internacional lo tenía. Sus primeros trabajos fueron reconocidos rápidamente por las instituciones más prestigiosas.
Entre sus galardones más destacados se encuentran el Premio Poncelet en 1886 y el Grand Prix des Sciences Mathématiques de la Academia de Ciencias en 1888. Estos premios consolidaron su reputación como el matemático líder de su generación en Francia.
Honores Nacionales y Distinciones Extranjeras
El reconocimiento a Picard trascendió las fronteras de las matemáticas y de Francia. Fue condecorado con la Grande Croix de la Légion d'Honneur en 1932, la más alta distinción de la República Francesa. Además, recibió la Medalla de Oro Mittag-Leffler, un premio internacional de gran prestigio en matemáticas.
Su influencia global se evidencia en su membresía honoraria en 37 sociedades científicas de todo el mundo y en los doctorados honoris causa que le otorgaron cinco universidades extranjeras. Fue un verdadero ciudadano del mundo de la ciencia, respetado y admirado por sus pares en todos los continentes.
Picard fue elegido miembro de la Academia de Ciencias de Francia en 1889, a la temprana edad de 33 años, un testimonio del impacto inmediato y profundo de su trabajo.
Estos honores no fueron solo personales; también reflejaron el resurgimiento de la escuela matemática francesa en la escena mundial, con Picard como uno de sus principales embajadores y protagonistas. Su liderazgo ayudó a definir la dirección de la investigación matemática durante décadas.
Pionero en Geometría Algebraica y Topología
La visión unificadora de Émile Picard se extendió más allá del análisis hacia la geometría algebraica. Su trabajo en esta área fue pionero y sentó las bases conceptuales para desarrollos futuros. Picard exploró la teoría de las superficies algebraicas y las funciones de dos variables complejas, un territorio vasto y poco explorado en su época.
Su colaboración con Georges Simart resultó en la monumental obra en dos volúmenes Théorie des fonctions algébriques de deux variables indépendantes, publicada entre 1897 y 1906. Este tratado sistematizó el estudio de las integrales en superficies algebraicas y estableció conexiones profundas con el análisis complejo, influyendo directamente en la escuela italiana de geometría algebraica.
El Grupo de Picard y las Integrales de Picard
Una de las contribuciones más perdurables de Picard en esta área es la introducción del concepto que hoy lleva su nombre: el grupo de Picard. Originalmente, Picard lo definió como un grupo de transformaciones relacionado con ecuaciones diferenciales lineales. Este concepto abstracto demostró ser extraordinariamente fértil.
En la geometría algebraica moderna, el grupo de Picard de una variedad algebraica clasifica los haces de línea sobre ella. Esta noción es central en la disciplina y un pilar en la investigación contemporánea. Las integrales que estudió, conocidas como integrales de Picard, también abrieron nuevas vías en el cálculo de períodos y en la teoría de Hodge.
El trabajo de Picard en superficies algebraicas fue descrito por sus contemporáneos como "iluminador", proporcionando el andamiaje algebraico necesario para estudiar objetos geométricos complejos de dimensión superior.
Su enfoque combinaba el rigor analítico con la intuición geométrica. Este estilo característico permitió que sus resultados trascendieran las barreras entre especialidades, creando un lenguaje común para matemáticos de diferentes campos. Su legado en este ámbito es tan sólido que sus términos y conceptos siguen en uso más de un siglo después.
Obras Magnas y su Impacto Educativo
Picard no fue solo un investigador genial; fue también un maestro y divulgador excepcional. Sus obras escritas se caracterizan por su claridad, exhaustividad y accesibilidad. Él creía firmemente que el conocimiento matemático avanzado debía ser comunicado de manera eficaz para prosperar.
Su Traîté d'analyse, publicado en tres volúmenes entre 1891 y 1896, se convirtió instantáneamente en un clásico. Este tratado cubría no solo análisis puro, sino también sus aplicaciones a problemas de elasticidad, teoría del calor y electricidad. Fue un texto de referencia para generaciones de estudiantes e investigadores en Francia y en el extranjero.
El Legado de un Expositor Claro
La habilidad pedagógica de Picard se refleja en la estructura lógica y la progresión gradual de sus libros. Sus escritos evitaban la oscuridad innecesaria, privilegiando una exposición que llevaba al lector desde los principios fundamentales hasta los teoremas más avanzados. Esta filosofía tuvo un impacto profundo en la educación matemática superior del siglo XX.
- Integración de Teoría y Aplicación: Sus textos mostraban constantemente cómo la matemática abstracta podía resolver problemas concretos de física e ingeniería.
- Formación de Futuros Investigadores: Muchos matemáticos prominentes de la siguiente generación aprendieron análisis y geometría directamente de los libros de Picard.
- Preservación Digital: Hoy, obras como sus notas de clase de 1891-1892 sobre cálculo integral están digitalizadas y disponibles en el Internet Archive, permitiendo que nuevas generaciones accedan a su enseñanza.
Además de sus tratados técnicos, Picard escribió biografías de colegas matemáticos franceses y uno de los primeros textos en francés sobre la teoría de la relatividad. Este compromiso con la historia y la filosofía de la ciencia completaba su perfil como un intelectual completo, preocupado por el contexto humano y cultural del descubrimiento científico.
Aplicaciones Prácticas e Influencia en la Física Matemática
La genialidad de Picard no se limitó a la torre de marfil de la matemática pura. Tenía un agudo interés por las aplicaciones prácticas de su trabajo. Creía que la elegancia de la teoría debía encontrar su contraparte en la utilidad para explicar el mundo natural y resolver problemas de ingeniería.
Una de sus contribuciones aplicadas más notables fue una solución elegante al problema de la transmisión de pulsos eléctricos en cables telegráficos. Este trabajo demostró cómo las ecuaciones diferenciales y el análisis complejo podían modelar y optimizar sistemas de comunicación, un campo de enorme importancia durante la Segunda Revolución Industrial.
Puente entre Disciplinas Científicas
Picard operó como un puente vital entre las matemáticas y otras ciencias. Sus métodos se aplicaron en la teoría de la elasticidad, ayudando a comprender la deformación de materiales. También trabajó en problemas relacionados con la propagación del calor, un área fundamental para la termodinámica y la ingeniería mecánica.
Picard representa el ideal del matemático del siglo XIX: un unificador que veía la teoría pura y la aplicada como dos caras de la misma moneda. Su obra es un testimonio del poder de las ideas abstractas para transformar la tecnología.
Esta visión integradora ha dejado una huella indeleble. Sus técnicas se emplean hoy en la física matemática moderna, particularmente en el estudio de ecuaciones no lineales como las ecuaciones de Painlevé. La fórmula Picard-Lefschetz, que surge de su trabajo en topología, es una herramienta esencial en la teoría de campos cuánticos y en la teoría de cuerdas, conectando su legado con la física teórica más avanzada del siglo XXI.
Liderazgo Académico y Contexto Histórico
La carrera de Picard se desarrolló en un período de grandes tensiones internacionales, particularmente entre Francia y Alemania. Su liderazgo científico estuvo inevitablemente marcado por este contexto. Tras la Primera Guerra Mundial, Picard jugó un papel central en el boicot científico a Alemania que duró desde 1917 hasta bien entrada la década de 1920.
Como secretario permanente de la Academia de Ciencias, utilizó su influencia para promover una política de aislamiento de los científicos alemanes. Esta postura, aunque controvertida hoy, reflejaba el intenso nacionalismo y el dolor de la posguerra en Francia. Fue una figura clave en la reorganización de la comunidad científica francesa tras el conflicto.
Un Hombre de Fe y Ciencia
Picard fue también un católico devoto en una época donde la relación entre fe y ciencia era a menudo tensa. No vio contradicción entre sus creencias religiosas y su trabajo científico. De hecho, fue miembro activo de organizaciones de científicos católicos y escribió sobre la compatibilidad de ambos mundos.
Su fe lo llevó a interesarse por la dimensión ética y filosófica del quehacer científico. Este aspecto de su pensamiento, menos conocido que sus teoremas, muestra la profundidad de un intelectual que reflexionaba sobre el lugar del hombre en el universo. Su biografía en Catholicscientists.org destaca precisamente este facetas de su vida.
- Secretario Permanente (1917-1941): Dirigió la Academia de Ciencias durante 24 años, moldeando la política científica francesa.
- Defensor de la "Ciencia Francesa": Promovió activamente los logros y el estilo nacional de hacer matemáticas.
- Mentor de una Nueva Generación: Bajo su tutela, se formaron numerosos matemáticos que continuaron su legado en análisis y geometría.
El contexto histórico de Picard es esencial para comprender la dimensión completa de su figura. Fue un producto de su tiempo: un patriota francés, un hombre de fe y un científico de ambición universal. Sus decisiones, tanto científicas como personales, estuvieron impregnadas de los valores y conflictos de la Europa de entresiglos.
El Legado Perdurable de Émile Picard
La influencia de Émile Picard en las matemáticas modernas es comparable a la de los gigantes en cuyos hombros se paró. Su capacidad para sintetizar ideas de análisis, geometría y álgebra creó un cuerpo de trabajo fundacional que sigue generando investigación más de un siglo después. Su legado no se mide solo en teoremas, sino en marcos conceptuales que redefinieron disciplinas enteras.
Los llamados teoremas de Picard siguen siendo herramientas esenciales en el análisis complejo contemporáneo. Su generalidad y profundidad los han convertido en resultados de referencia, presentes en todos los textos serios sobre la materia. Son un testamento del poder del pensamiento abstracto para revelar verdades universales sobre las funciones.
Impacto en la Investigación Contemporánea
En el siglo XXI, las ideas de Picard siguen vivas en áreas de vanguardia. En topología algebraica, la fórmula Picard-Lefschetz es fundamental para entender la monodromía y los ciclos evanescentes. Esta conexión entre su trabajo en análisis y la topología moderna ilustra la previsión extraordinaria de su pensamiento.
En el campo computacional, el método de iteración de Picard es un algoritmo básico en el análisis numérico de ecuaciones diferenciales. Está implementado en bibliotecas de software como MATLAB y SciPy, utilizadas por millones de ingenieros y científicos para resolver problemas prácticos en física, biología y finanzas.
- Teoría de Funciones: Sus teoremas se aplican en el estudio de dinámicas complejas y sistemas dinámicos.
- Geometría Algebraica Moderna: El grupo de Picard es un invariante central en la clasificación de variedades algebraicas.
- Física Matemática: Sus técnicas aparecen en la teoría de ecuaciones integrables y sistemas Hamiltonianos.
El matemático Jean Dieudonné señaló que Picard "poseía el don raro de ver las conexiones profundas entre campos aparentemente dispares de las matemáticas". Esta visión unificadora es quizás su contribución más valiosa y perdurable.
Su obra escrita, especialmente el Traîté d'analyse, sigue siendo estudiada no solo por su contenido histórico, sino por la claridad ejemplar de su exposición. Muchos de los enfoques pedagógicos que introdujo se han convertido en estándar en la enseñanza de las matemáticas avanzadas.
El Visionario y su Visión Unificadora de la Ciencia
Picard encarnó el ideal del científico integral del siglo XIX. No reconocía barreras rígidas entre la matemática pura y aplicada, ni entre disciplinas teóricas. Para él, el análisis, el álgebra y la geometría eran facetas de una sola verdad matemática que podía, a su vez, iluminar los fenómenos naturales.
Esta visión holística lo llevó a contribuir en campos tan diversos como la telegrafía, la elasticidad y la teoría del calor. Abordó cada problema con el mismo rigor y elegancia, estableciendo un estándar de excelencia que influyó en generaciones de científicos franceses y europeos.
Una Filosofía de la Ciencia Integrada
Picard creía en la unidad del conocimiento. Su trabajo biográfico sobre otros matemáticos refleja su interés por el contexto humano e histórico del descubrimiento científico. Escribió sobre la relatividad cuando esta teoría era aún novedosa, demostrando una curiosidad intelectual que trascendía su especialización inmediata.
Su fe católica no era un aspecto separado de su vida científica, sino parte de una cosmovisión coherente. En una época de creciente especialización y secularización, Picard defendió la posibilidad de una mente científica que también fuera espiritual. Esta integridad personal añade una dimensión profundamente humana a su legado.
Como líder académico durante más de dos décadas en la Academia de Ciencias, promovió activamente esta visión de ciencia unificada. Apoyó investigaciones que cruzaban fronteras disciplinarias y fomentó colaboraciones entre matemáticos, físicos e ingenieros. Su liderazgo ayudó a definir la identidad de la ciencia francesa en la escena internacional durante un período crucial.
Conclusión: La Huella Indeleble de un Genio
Émile Picard falleció el 11 de diciembre de 1941, en un París ocupado por las fuerzas nazis. Su muerte marcó el final de una era en las matemáticas francesas. Sin embargo, sus ideas habían trascendido ya las fronteras de su tiempo y de su nación, convirtiéndose en patrimonio universal de la ciencia.
La evaluación histórica de su obra solo ha crecido con el tiempo. Donde sus contemporáneos veían teoremas brillantes, las generaciones posteriores han descubierto estructuras profundas y conexiones fecundas. Su nombre está grabado en conceptos fundamentales que los matemáticos usan a diario en laboratorios y aulas de todo el mundo.
Resumen de Contribuciones Clave
El legado de Picard puede resumirse en varias contribuciones monumentales que transformaron permanentemente el paisaje matemático:
- Teoremas de Picard: Resultados fundamentales en análisis complejo sobre el rango de funciones enteras y el comportamiento cerca de singularidades esenciales.
- Método de Iteración de Picard: Una herramienta constructiva para probar existencia y unicidad de soluciones a ecuaciones diferenciales, con aplicaciones prácticas inmediatas.
- Grupo de Picard: Un concepto algebraico-geométrico central en la clasificación de variedades algebraicas, con ramificaciones en topología y física teórica.
- Obra Expositiva Magistral: Tratados que educaron a generaciones de matemáticos y establecieron estándares de claridad y rigor.
- Visión Unificadora: La demostración práctica de cómo la matemática pura y aplicada pueden enriquecerse mutuamente.
El obituario de la Royal Society of Edinburgh destacó que Picard "combinaba una potencia creativa excepcional con un dominio técnico consumado y una claridad expositiva rara vez igualada". Esta triple combinación explica la profundidad y longevidad de su impacto.
Relevancia en el Siglo XXI
En la era digital del siglo XXI, la visión de Picard resulta más pertinente que nunca. La explosión de datos y la complejidad de los sistemas modernos requieren exactamente el tipo de pensamiento interdisciplinario que él practicó. Sus métodos numéricos están en el corazón de algoritmos que modelan desde el clima global hasta los mercados financieros.
Su insistencia en la claridad expositiva anticipó la importancia actual de la comunicación científica efectiva. En un mundo saturado de información, la capacidad de articular ideas complejas con precisión y elegancia es más valiosa que nunca. Picard fue un maestro de este arte.
Finalmente, su ejemplo como científico con una visión ética y filosófica del mundo ofrece un modelo inspirador. En una época de especialización extrema y frecuente divorcio entre la ciencia y las humanidades, Picard demostró que es posible, y deseable, cultivar una mente científica integral.
Reflexión Final: El Matemático Completo
Charles-Émile Picard fue mucho más que el autor de algunos teoremas brillantes. Fue un arquitecto intelectual que ayudó a construir los cimientos de las matemáticas modernas. Su trabajo conectó análisis con geometría, teoría con aplicación, y el siglo XIX con el futuro de la disciplina.
Su vida nos recuerda que los avances científicos más significativos a menudo provienen de mentes que se niegan a ser confinadas por las fronteras artificiales entre campos. La curiosidad sin límites y la búsqueda de conexiones profundas fueron las fuerzas motrices de su genio.
Hoy, cuando los matemáticos aplican el teorema de Picard para estudiar fractales, cuando los físicos usan la fórmula Picard-Lefschetz en teoría cuántica de campos, o cuando los ingenieros implementan su método de iteración en software de simulación, están participando de un legado que comenzó en la mente de un visionario parisino del siglo XIX. La obra de Émile Picard vive en cada uno de estos descubrimientos y aplicaciones, un testimonio permanente del poder transformador de las ideas matemáticas cuando son concebidas con profundidad, claridad y una visión amplia del mundo.
Su historia es un recordatorio de que la verdadera grandeza en la ciencia no se mide solo por resultados específicos, sino por la capacidad de abrir nuevos caminos de pensamiento para quienes vendrán después. En este sentido, Picard fue, y sigue siendo, un verdadero gigante cuyos hombros aún sostienen a los exploradores del conocimiento matemático.
Jacques Hadamard: Un Genio Matemático de Proporciones Iniguales
Jacques Hadamard fue un matemático francés cuya genialidad excepcional transformó múltiples campos del análisis matemático y dejó una huella perdurable en la ciencia. Reconocido mundialmente por probar el teorema de los números primos, su legado abarca desde ecuaciones diferenciales hasta la computación cuántica moderna. Este artículo explora la vida y las contribuciones inigualables de un genio cuyas ideas continúan resonando en el siglo XXI.
La Formación Temprana de un Prodigio
Jacques-Salomon Hadamard nació el 8 de diciembre de 1865 en Versalles, Francia. Desde una edad muy temprana, su talento intelectual fue evidente, destacando notablemente en el prestigioso Concours Général a partir de 1875. Este entorno académico riguroso fue el crisol donde se forjó su futuro como uno de los grandes matemáticos de su tiempo.
El Camino Hacia el Doctorado y el Primer Gran Reconocimiento
Hadamard se formó en la célebre École Normale Supérieure, donde desarrolló una profunda pasión por el análisis complejo. En 1892, obtuvo su doctorado con una tesis sobre funciones definidas por series de Taylor. El joven investigador no tardó en captar la atención de la comunidad científica, ganando el Grand Prix des Sciences Mathématiques por su ensayo sobre la función zeta de Riemann.
Este premio fue solo el comienzo de una carrera llena de logros. Su trabajo doctoral sentó las bases para sus futuras exploraciones en áreas tan diversas como las ecuaciones diferenciales y el análisis funcional. La precisión y profundidad de sus primeros trabajos ya anunciaban el genio de proporciones iniguales en el que se convertiría.
Su tesis doctoral y el ensayo premiado sobre la función zeta evidenciaron una capacidad analítica fuera de lo común, marcando el inicio de una producción científica monumental.
La Demostración Histórica del Teorema de los Números Primos
El año 1896 se convertiría en un hito en la historia de las matemáticas. De manera independiente a Charles-Jean de la Vallée Poussin, Jacques Hadamard consiguió demostrar el emblemático teorema de los números primos. Este resultado, largamente conjeturado, describe la distribución asintótica de los números primos.
El teorema establece formalmente que, si π(n) denota la cantidad de números primos menores o iguales a n, entonces se cumple la aproximación:
π(n) ≈ n / ln(n) a medida que n → ∞.
Esta demostración no solo resolvía uno de los problemas más importantes de la teoría de números del siglo XIX, sino que consolidó a Hadamard como una figura de primer orden en el panorama matemático mundial. El uso de métodos del análisis complejo para resolver un problema de teoría de números fue considerado una hazaña de gran ingenio.
Las Consecuencias y el Impacto del Teorema
La prueba del teorema tuvo un impacto revolucionario. Validó definitivamente la conexión profunda entre la teoría analítica de números y la función zeta de Riemann. Este logro le valió importantes reconocimientos, como el Premio Bordin en 1896, y estableció un nuevo estándar en la investigación matemática.
- Solución a un problema centenario: Confirmó matemáticamente la intuición de Gauss y Legendre sobre la distribución de los primos.
- Síntesis de disciplinas: Fusionó la teoría de números con el análisis complejo, abriendo nuevas vías de investigación.
- Reconocimiento inmediato: Secundado por el premio Bordin, situó a Hadamard en la élite científica francesa e internacional.
La Desigualdad de Hadamard y las Matrices que Llevan su Nombre
En 1893, tres años antes de su gran teorema, Hadamard ya había hecho otra contribución fundamental. Publicó su famosa desigualdad de Hadamard, un resultado elegante y poderoso para los determinantes de ciertas matrices. Este trabajo es la piedra angular de las ahora conocidas como matrices de Hadamard.
Una matriz de Hadamard es una matriz cuadrada cuyas entradas son +1 o -1 y cuyas filas son mutuamente ortogonales. La desigualdad establece un límite superior absoluto para el valor del determinante de una matriz con entradas complejas acotadas en módulo.
La relevancia de este descubrimiento fue más allá de las matemáticas puras. Las matrices de Hadamard encontraron aplicaciones prácticas en:
- Teoría de códigos y señales: Optimizando transmisiones y minimizando errores.
- Ecuaciones integrales: Proporcionando herramientas para su resolución.
- Computación cuántica: Siendo la base de la puerta de Hadamard, una operación fundamental en los algoritmos cuánticos.
La desigualdad de 1893 demostró la capacidad de Hadamard para crear conceptos abstractos con aplicaciones prácticas de largo alcance, trascendiendo su propia época.
La Vida Personal y el Contexto Histórico
La vida de Jacques Hadamard estuvo profundamente entrelazada con los acontecimientos históricos de su época. En 1896, el mismo año de su gran demostración, contrajo matrimonio con su novia de infancia. Su etapa profesional en Burdeos, de 1893 a 1897, fue particularmente prolífica. Allí ocupó una cátedra de astronomía y mecánica racional y publicó la asombrosa cantidad de 29 trabajos profundos en temas muy variados.
Compromiso Político y la Huida del Régimen de Vichy
Hadamard, de origen judío, fue un activista comprometido. Participó activamente en la defensa de Alfred Dreyfus durante el famoso caso que dividió a Francia, combatiendo el antisemitismo desde su posición de prestigio. Este compromiso social y político marcó su carácter tanto como sus logros académicos.
Su carrera docente prosiguió en instituciones de élite como la Sorbona y el Collège de France, donde sucedió al gran Henri Poincaré en la Academia de Ciencias en 1912. Sin embargo, la Segunda Guerra Mundial truncó su vida en Europa. En 1941, huyendo del régimen de Vichy, se exilió en los Estados Unidos, donde trabajó en la Universidad de Columbia. Su pensamiento, sin embargo, trascendía fronteras e influyó en movimientos posteriores como el grupo Bourbaki.
La primera parte de la vida y obra de Jacques Hadamard revela al genio matemático de proporciones iniguales que forjó herramientas abstractas con consecuencias prácticas eternas. Su dominio del análisis funcional, su rigor en la teoría de números y su creatividad inagotable son solo la introducción a un legado que continúa en pleno siglo XXI.
Contribuciones Clave en Análisis y Ecuaciones Diferenciales
La vasta obra de Jacques Hadamard se extiende mucho más allá del teorema de los números primos. Sus contribuciones al análisis funcional y a la teoría de las ecuaciones diferenciales parciales fueron igualmente revolucionarias y cimentaron su estatus de pensador total en matemáticas. Su capacidad para abordar problemas fundamentales desde ángulos novedosos transformó estas disciplinas.
El Concepto de Problema Bien Planteado
Una de las ideas más influyentes de Hadamard es la noción de un "problema bien planteado" en el contexto de las ecuaciones diferenciales parciales. Postuló que para que un problema matemático tenga significado físico y sea resoluble, debe cumplir tres condiciones esenciales. Esta conceptualización disciplinó el campo y guió generaciones de investigadores.
- Existencia de una solución: Debe existir al menos una solución al problema planteado.
- Unicidad de la solución: Esa solución debe ser única bajo las condiciones dadas.
- Dependencia continua de los datos: La solución debe cambiar de forma continua con cambios pequeños en las condiciones iniciales o de contorno.
Este marco conceptual no solo fue teórico; proporcionó un criterio riguroso para evaluar la validez de modelos en física matemática e ingeniería. Muchos problemas que antes parecían intratables pudieron ser reformulados siguiendo los principios de Hadamard.
La definición de problemas bien planteados por Hadamard es una piedra angular en la formulación matemática de fenómenos físicos, asegurando soluciones significativas y estables.
Fundamentos del Análisis Funcional y el Cálculo de Variaciones
Hadamard fue un pionero en el desarrollo temprano del análisis funcional, un área que estudia espacios de funciones y operadores. Su libro "Leçons sur le calcul des variations", publicado en 1910, es considerado una obra fundacional. En ella, sistematizó y expandió el cálculo de variaciones, conectándolo con ideas emergentes en topología y análisis.
Su trabajo en esta área sentó las bases para desarrollos posteriores de figuras como Banach y Hilbert. Hadamard comprendió que muchos problemas de análisis clásico podían reformularse de manera más clara y poderosa dentro del contexto de espacios funcionales de dimensión infinita. Esta visión abstracta y unificadora es característica de su genio.
Por sus múltiples contribuciones, recibió premios de la más alta distinción, como el Premio Poncelet en 1898. Además, su liderazgo fue reconocido con la presidencia de la Sociedad Matemática de Francia en 1906 y una cátedra permanente en el prestigioso Collège de France.
El Legado en Psicología de la Creatividad Matemática
Además de su producción puramente matemática, Hadamard dedicó una profunda reflexión al proceso mismo del descubrimiento. Su libro de 1945, "Psychology of Invention in the Mathematical Field", es un estudio seminal sobre la creatividad. En él, investigó los procesos mentales subyacentes a los momentos de insight y descubrimiento científico.
Las Entrevistas a Grandes Figuras y el Modelo de Dos Etapas
Hadamard basó su investigación en entrevistas personales con algunos de los grandes matemáticos y físicos de su tiempo, incluidos Henri Poincaré y Albert Einstein. A partir de estos testimonios, propuso un modelo de creatividad en dos etapas que sigue siendo relevante en la filosofía de la mente y la ciencia cognitiva actual.
- Etapa de Generación (Inconsciente): Una fase de incubación donde la mente, de forma subconsciente, combina ideas y conceptos de manera libre y caótica.
- Etapa de Selección (Consciente): Un momento de iluminación o "Eureka" donde una idea coherente emerge a la conciencia para ser examinada y verificada lógicamente.
Hadamard argumentó que el trabajo inconsciente es fundamental para la innovación. Su análisis conectaba la creatividad matemática con procesos psicológicos universales, desmitificando la idea del genio como un mero ejercicio de lógica fría y consciente.
Su modelo de dos etapas para la invención matemática ha influido en estudios modernos sobre libre albedrío, innovación y los procesos cerebrales detrás del pensamiento creativo.
Influencia y Aplicaciones en la Ciencia Moderna
El impacto del trabajo de Jacques Hadamard no se detuvo en el siglo XX. Por el contrario, sus conceptos y herramientas encuentran aplicaciones vibrantes en tecnologías de vanguardia como la computación cuántica y el procesamiento de señales. Esta capacidad de trascender su época es el sello de un verdadero visionario.
La Puerta de Hadamard en Computación Cuántica
Quizás la aplicación más fascinante y contemporánea de su legado es la puerta de Hadamard en computación cuántica. Esta operación fundamental actúa sobre un qubit, la unidad básica de información cuántica. La puerta crea un estado de superposición, permitiendo al qubit estar simultáneamente en un estado |0⟩ y |1⟩ con igual probabilidad.
Esta transformación, inspirada directamente en las matrices de Hadamard, es la base de algoritmos cuánticos poderosos, como el algoritmo de búsqueda de Grover y el algoritmo de factorización de Shor. La conexión es profunda: la ortogonalidad y las propiedades espectrales de sus matrices del siglo XIX resultaron ser ideales para manipular la superposición cuántica.
- Base de algoritmos cuánticos: Es una operación esencial para lograr el paralelismo cuántico.
- Conexión matemática directa: Implementa físicamente las propiedades de las matrices que él estudió.
- Legado en tecnología futura: Coloca a Hadamard como una figura paterna indirecta de un campo científico revolucionario.
Aplicaciones en Teoría de Códigos y Procesamiento de Señales
En el ámbito de las comunicaciones y el procesamiento digital, las matrices de Hadamard son indispensables. Se utilizan en la construcción de códigos de corrección de errores, como los códigos de Reed-Muller, que protegen la integridad de los datos en transmisiones satelitales y almacenamiento digital. Su propiedad de ortogonalidad permite separar señales de manera eficiente.
En el procesamiento de imágenes y señales, la transformada de Walsh-Hadamard es una herramienta fundamental para la compresión y el análisis espectral. Es una versión más simple y computacionalmente eficiente que la transformada de Fourier, ampliamente utilizada en algoritmos de compresión de video y en procesamiento de señales de radar.
La versatilidad y utilidad práctica de un concepto matemático puro inventado por Hadamard es un testimonio de su profunda intuición. Sus ideas no solo resolvieron problemas abstractos, sino que también diseñaron, sin saberlo, las herramientas para tecnologías futuras.
Desde los satélites que orbitan la Tierra hasta los laboratorios de computación cuántica, el trabajo de Hadamard proporciona una infraestructura matemática crítica para la tecnología moderna.
Esta segunda parte del recorrido por la vida de Jacques Hadamard revela la asombrosa amplitud de su mente. Desde los fundamentos del análisis hasta los secretos de la creatividad y las aplicaciones tecnológicas más avanzadas, su legado es un monumento al pensamiento matemático puro y aplicado. Su figura se agiganta como la de un verdadero arquitecto del conocimiento científico del siglo XX y más allá.
La Productividad y los Reconocimientos de un Genio Incansable
La carrera de Jacques Hadamard se caracterizó por una productividad asombrosa y sostenida a lo largo de más de siete décadas. Sus períodos más intensos, como su estancia en Burdeos, fueron verdaderas tormentas de creatividad matemática. Los datos cuantitativos de su producción ofrecen una perspectiva clara de la magnitud de su genio y dedicación.
Una Producción Científica Monumental
Entre los años 1893 y 1897, mientras ocupaba un puesto en Burdeos, Hadamard publicó la impresionante cantidad de 29 trabajos científicos profundos. Estos artículos no fueron meras notas triviales; abordaron temas fundamentales y variados, desde el análisis complejo hasta la teoría de números y las ecuaciones diferenciales. Esta etapa demostró su capacidad para trabajar en múltiples frentes con igual maestría.
A lo largo de su vida, su producción no decayó. Publicó cientos de artículos y varios libros fundamentales. Esta enorme productividad se explica no solo por su talento innato, sino también por su método riguroso y su habilidad para identificar problemas centrales en cada campo que tocaba. Su obra escrita es un mapa del pensamiento matemático avanzado de su época.
- 29 trabajos en 5 años (Burdeos): Una media de casi seis publicaciones de alto impacto por año.
- Libros fundacionales: Como "Leçons sur le calcul des variations" (1910) y su obra sobre psicología de la invención (1945).
- Amplitud temática: Sus publicaciones cubrieron análisis, teoría de números, física matemática y filosofía de la ciencia.
Premios y Posiciones de Liderazgo
El reconocimiento a su trabajo llegó pronto y se mantuvo constante. Hadamard acumuló los más altos honores que el mundo académico francés e internacional podía otorgar. Estos premios no fueron solo distinciones personales, sino indicadores del valor transformador de sus contribuciones para las matemáticas como disciplina.
La trayectoria de premios de Hadamard —desde el Grand Prix hasta la silla en el Collège de France— es un testimonio del respeto unánime que inspiró entre sus contemporáneos.
Sus posiciones de liderazgo fueron igualmente destacadas. Suceder a Henri Poincaré, uno de los últimos polímatas universales, en la Academia de Ciencias en 1912, fue un reconocimiento simbólico de que él mismo ocupaba ese estatus. Como presidente de la Sociedad Matemática de Francia, guió la comunidad científica durante un período de gran fermentación intelectual.
El Legado Perdurable y su Estudio Contemporáneo
La influencia de Jacques Hadamard no se ha desvanecido con el tiempo. Por el contrario, su legado se estudia, se analiza y se celebra en formatos modernos y accesibles. Su vida y obra continúan inspirando a nuevas generaciones de matemáticos, científicos e incluso público general interesado en la historia de las ideas.
Hadamard en la Cultura Digital y los Medios Modernos
El legado de este genio matemático ha encontrado un nuevo hogar en la era digital. En 2023, por ejemplo, se publicaron videos y podcasts educativos dedicados a desglosar su vida y sus contribuciones más importantes. Estos recursos hacen que su trabajo sea más accesible y demuestran el interés continuo en figuras que moldearon nuestra comprensión del mundo.
Biografías en línea, artículos de divulgación y entradas en enciclopedias digitales mantienen viva su memoria. Este fenómeno subraya una verdad fundamental: las contribuciones de Hadamard tienen una calidad atemporal. Sus definiciones, teoremas y marcos conceptuales son tan claros y potentes hoy como lo fueron hace un siglo.
- Podcasts y documentales: Análisis modernos de su vida, como el video biográfico de 2023, que llegan a una audiencia global.
- Recursos educativos en línea: Sus conceptos se enseñan en cursos digitales de análisis funcional, teoría de números y computación cuántica.
- Inspiración permanente: Sigue siendo citado como ejemplo de profundidad, amplitud y creatividad científica.
Influencia en Escuelas de Pensamiento y en el Grupo Bourbaki
La forma de hacer matemáticas de Hadamard, con su énfasis en el rigor, la generalidad y la claridad estructural, influyó profundamente en el nacimiento del influyente grupo Bourbaki en la década de 1930. Este colectivo de matemáticos franceses buscaba refundar las matemáticas sobre bases axiomáticas sólidas, un espíritu que resonaba con el trabajo sistematizador de Hadamard en análisis funcional.
Su idea de los problemas bien planteados se convirtió en un estándar en el análisis de ecuaciones diferenciales parciales, disciplina fundamental para la física teórica y la ingeniería. Su enfoque abstracto pero rigurosamente fundamentado ayudó a pivotar las matemáticas del siglo XX hacia una mayor abstracción, sin perder de vista las aplicaciones.
Conclusión: El Arquitecto del Pensamiento Matemático Moderno
Al repasar la vida y obra de Jacques Hadamard, surge la imagen de un arquitecto intelectual de proporciones inigualables. Su genio no residió en un solo descubrimiento espectacular, sino en una serie de contribuciones fundamentales que redefinieron múltiples campos. Hadamard fue un puente entre el siglo XIX y el XX, entre la matemática clásica y la moderna, y entre la teoría pura y sus aplicaciones más insospechadas.
Las Claves del Genio de Hadamard
Podemos resumir su grandeza en varios pilares interconectados que explican por qué su legado es tan perdurable y respetado.
- Amplitud Excepcional: Dominó y contribuyó de forma decisiva a la teoría de números, el análisis complejo, las ecuaciones diferenciales, el análisis funcional y el cálculo de variaciones.
- Profundidad y Rigor: Cada uno de sus trabajos se caracteriza por un nivel de profundidad y un rigor lógico implacable que los convirtió en referentes obligados.
- Capacidad de Fundamentación: Tuvo el don de establecer los cimientos de nuevas áreas, como con el concepto de problema bien planteado o las bases del análisis funcional.
- Intuición para la Utilidad: Conceptos abstractos que él investigó, como las matrices que llevan su nombre, encontraron décadas después aplicaciones cruciales en tecnología de vanguardia.
- Reflexión sobre el Proceso Creativo: Trascendió la mera producción para analizar filosóficamente cómo ocurre la invención matemática, legándonos insights valiosos sobre la mente creativa.
Jacques Hadamard encarnó la unión perfecta entre el pensador abstracto más puro y el arquitecto de herramientas que, en última instancia, modelan nuestro mundo tecnológico.
Un Legado que Trasciende las Matemáticas
Finalmente, la figura de Hadamard trasciende el ámbito estricto de las matemáticas. Su activismo en el caso Dreyfus nos habla de un científico comprometido con la justicia y la verdad en el ámbito social. Su exilio durante la guerra refleja los trastornos del siglo XX que impactaron incluso a las mentes más brillantes. Y su libro sobre psicología de la invención lo conecta con las humanidades y las ciencias cognitivas.
Hoy, cuando un científico enuncia un problema bien planteado, cuando un ingeniero utiliza un código para proteger datos, o cuando un físico cuántico aplica una puerta de Hadamard a un qubit, están, conscientemente o no, caminando sobre los cimientos que este genio francés ayudó a construir. Jacques Hadamard no solo resolvió ecuaciones y demostró teoremas; dio forma a la forma misma en que pensamos sobre problemas complejos.
Su historia es un recordatorio poderoso de que la búsqueda más abstracta del conocimiento puro puede, con el tiempo, revelarse como la fuente más práctica para las revoluciones tecnológicas y conceptuales del futuro. Por eso, Jacques Hadamard sigue siendo, y seguirá siendo, un genio matemático de proporciones verdaderamente inigualables.


Henri Lebesgue: El Arquitecto del Análisis Moderno
En el paisaje de las matemáticas del siglo XX, Henri Lebesgue se erige como una figura monumental. Sus revolucionarias contribuciones a la teoría de la medida y la integración le valieron el título de arquitecto del análisis matemático moderno. Su trabajo trascendió las limitaciones de los siglos anteriores, proporcionando herramientas esenciales para dominios tan diversos como la física cuántica y el machine learning. Esta es la historia del genio que redefinió el cálculo integral.
Los Cimientos de una Revolución Matemática
Para entender la magnitud de la obra de Lebesgue, es esencial comprender el contexto histórico en el que surgió. El cálculo integral, fundamentado por Newton y Leibniz en el siglo XVII, y luego refinado por Riemann en el XIX, presentaba una debilidad crucial. Estos métodos estaban diseñados para funciones continuas y bien comportadas, pero fallaban espectacularmente ante funciones con discontinuidades complejas. El mundo matemático necesitaba una teoría más poderosa y flexible.
La tesis de Lebesgue, "Intégrale, longueur, aire", presentada en 1902, no fue solo un doctorado: fue un nuevo cimiento para el análisis.
Fue en este escenario donde Henri Lebesgue, inspirado por las ideas de sus predecesores Émile Borel y Camille Jordan, ideó su genial enfoque. Mientras la integral de Riemann dividía el dominio de la función, la innovación de Lebesgue fue enfocarse en su codominio o rango. Este cambio de perspectiva, aparentemente sencillo, permitió medir conjuntos mucho más complejos y, en consecuencia, integrar una clase de funciones vastamente más amplia.
Una Vida Dedicada a la Precisión
Henri Léon Lebesgue nació el 28 de junio de 1875 en Beauvais, Francia, en el seno de una familia de humildes condiciones. Su brillantez intelectual fue su pasaporte para ingresar a la prestigiosa École Normale Supérieure y posteriormente a la Sorbona, donde estudió bajo la tutela de Émile Borel. Su carrera docente comenzó en el Lycée Central de Nancy (1899-1902) y culminó en cátedras de gran prestigio en la Sorbona (1910) y finalmente en el Collège de France (1920).
Su legado no se limita a sus publicaciones; también fue un educador comprometido. Tras 1922, dedicó una parte significativa de su energía a la enseñanza y a la geometría elemental, consolidando su impacto en varias generaciones de matemáticos. A lo largo de su vida, recibió numerosos reconocimientos, incluyendo el Prix Houllevigue (1912) y el Prix Poncelet (1914), que atestiguan la importancia temprana de su trabajo.
La Integral de Lebesgue: Un Cambio de Paradigma
El concepto central de la revolución lebeguiana es, sin duda, la integral de Lebesgue. Pero para llegar a ella, primero tuvo que crear una herramienta más fundamental: la teoría de la medida. La medida lebesguiana proporciona una manera rigurosa y general de asignar un "tamaño" o "volumen" a conjuntos, incluso a aquellos con estructuras muy intrincadas y no necesariamente continuas.
La construcción de su integral sigue un proceso lógico y elegante:
- Paso 1: Se define la integral para funciones simples (que toman un número finito de valores).
- Paso 2: Utilizando la medida, se aproximan funciones más complejas mediante sucesiones de funciones simples.
- Paso 3: Se define la integral de la función compleja como el límite de las integrales de las funciones simples que la aproximan.
Ventajas Clave sobre la Integral de Riemann
Este método superó las deficiencias del pasado de manera contundente. Estas son las principales ventajas de la integral de Lebesgue:
- Mayor Generalidad: Integra una clase mucho más amplia de funciones, incluyendo muchas con infinitas discontinuidades.
- Teoremas de Convergencia Potentes: Permite intercambiar límites e integrales bajo condiciones menos restrictivas (Teorema de la Convergencia Monótona, Teorema de la Convergencia Dominada).
- Completitud del Espacio: El espacio de funciones integrables según Lebesgue (espacio L^p) es completo, una propiedad fundamental para el análisis funcional.
- Cimientos para Otras Teorías: Se convirtió en la base indispensable para la teoría de probabilidades axiomática de Kolmogórov, el análisis de Fourier moderno y el estudio de ecuaciones en derivadas parciales.
La integral de Lebesgue revolucionó el análisis al extender su alcance más allá de las funciones continuas, un avance que más del 90% de los matemáticos actuales consideran fundamental para su campo.
Aplicaciones Inmediatas y Teoremas Fundacionales
El impacto de la nueva teoría fue rápido y profundo. Lebesgue mismo aplicó sus herramientas para resolver problemas pendientes y establecer resultados que hoy son pilares del currículo matemático.
El Lema de Riemann-Lebesgue y las Series de Fourier
En 1905, Lebesgue utilizó su integral para probar un resultado crucial ahora conocido como el lema de Riemann-Lebesgue. Este lema establece que los coeficientes de Fourier de una función integrable (en el sentido de Lebesgue) tienden a cero. Fue un avance monumental en la teoría de series de Fourier, proporcionando claridad sobre los límites de convergencia y sentando las bases para el análisis armónico moderno.
Su integral permitió un tratamiento riguroso de la convergencia de las series de Fourier para clases de funciones mucho más generales, resolviendo problemas que habían desconcertado a los matemáticos durante décadas.
El Teorema de Diferenciación de Lebesgue
Publicado en 1912, el teorema de diferenciación de Lebesgue es otro pilar del análisis real. En esencia, afirma que para una función localmente integrable (según Lebesgue), en casi todo punto (es decir, excepto en un conjunto de medida cero), la función es diferenciable y su derivada puede recuperarse promediando sobre intervalos que se contraen al punto.
Este teorema conecta profundamente los procesos de integración y diferenciación en un contexto generalizado y es fundamental en campos como la teoría del potencial y las ecuaciones diferenciales. Su trabajo en esta área demostró el poder unificador de su teoría de la medida.
El Legado de Lebesgue en la Teoría Matemática Moderna
Si bien la teoría de la medida y la integral son sus contribuciones más famosas, la influencia de Henri Lebesgue se extiende a otras áreas fundamentales de las matemáticas. Su trabajo no fue aislado, sino que proporcionó las herramientas para que otras disciplinas avanzaran de manera significativa. Su visión integral del análisis sentó las bases para desarrollos posteriores en topología, teoría de probabilidades y análisis funcional.
Uno de sus aportes menos conocidos pero igualmente importantes fue su trabajo en el principio de teselado e invariancia dimensional en 1921. Este principio establece resultados cruciales sobre cómo los espacios pueden ser divididos y cómo se conserva su dimensión bajo ciertas transformaciones. Sus investigaciones en este campo fueron un avance seminal que influyó directamente en el desarrollo de la topología moderna.
Impacto en la Teoría de Probabilidades Axiomática
La conexión entre la teoría de Lebesgue y la probabilidad es profunda e inseparable. Cuando Andrei Kolmogórov formuló los fundamentos axiomáticos de la teoría de probabilidades en 1933, utilizó la teoría de la medida como su columna vertebral. La medida de Lebesgue proporcionó el marco matemático riguroso necesario para definir conceptos como:
- Espacios de probabilidad como espacios de medida con medida total 1
- Variables aleatorias como funciones medibles
- Valor esperado como integrales de Lebesgue
- Convergencia casi segura basada en el concepto de "casi todo punto"
La probabilidad moderna sería inconcebible sin la integral de Lebesgue. Más del 95% de los textos avanzados de teoría de probabilidades utilizan el marco de la medida de Lebesgue como fundamento.
Aplicaciones Prácticas en la Ciencia y Tecnología Contemporáneas
La relevancia del trabajo de Lebesgue trasciende las matemáticas puras y tiene aplicaciones concretas en múltiples campos científicos y tecnológicos. Lo que comenzó como una abstracción matemática hoy impulsa avances en áreas que afectan nuestra vida diaria, desde la inteligencia artificial hasta las comunicaciones digitales.
Machine Learning y Ciencia de Datos
En el campo del machine learning y la ciencia de datos, la integral de Lebesgue proporciona los fundamentos teóricos para muchos algoritmos modernos. Los espacios de funciones integrables (espacios L^p) son esenciales para:
- Teoría de optimización en redes neuronales profundas
- Análisis de convergencia de algoritmos de aprendizaje
- Procesamiento de señales y análisis espectral
- Modelos estocásticos en aprendizaje automático
La capacidad de trabajar con funciones que pueden tener discontinuidades o comportamientos patológicos permite a los científicos de datos modelar fenómenos del mundo real con mayor precisión. La teoría de la medida subyace en conceptos avanzados como las máquinas de vectores de soporte y los procesos gaussianos.
Física Teórica y Ingeniería
En física, particularmente en mecánica cuántica y teoría cuántica de campos, la integral de Lebesgue es indispensable. La formulación matemática de la mecánica cuántica utiliza espacios de Hilbert, que son completos respecto a la norma definida por la integral de Lebesgue. Aplicaciones específicas incluyen:
- Ecuaciones de Schrödinger y operadores no acotados
- Teoría espectral de operadores en mecánica cuántica
- Integrales de camino de Feynman en teoría cuántica de campos
- Análisis de Fourier avanzado en procesamiento de imágenes médicas
En ingeniería eléctrica, el procesamiento digital de señales depende críticamente del análisis de Fourier, que a su vez se beneficia de la mayor generalidad proporcionada por la integral de Lebesgue. Esto permite el análisis de señales que no serían tratables con los métodos clásicos de Riemann.
Reconocimiento y Legado Académico
El impacto duradero del trabajo de Lebesgue se refleja no solo en sus aplicaciones prácticas, sino también en el reconocimiento continuo que recibe dentro de la comunidad matemática mundial. A pesar de haber fallecido en 1941, su influencia sigue creciendo y su nombre permanece entre los más respetados en la historia de las matemáticas.
Premios y Distinciones
A lo largo de su carrera, Lebesgue recibió numerosos premios que attestiguan la importancia de sus contribuciones. Entre los más destacados se encuentran:
- Prix Houllevigue (1912) por sus trabajos sobre integración
- Prix Poncelet (1914) de la Academia de Ciencias de Francia
- Prix Saintour (1917) por sus contribuciones matemáticas
- Prix Petit d'Ormoy en fecha no especificada
- Miembro Extranjero de la Royal Society (ForMemRS)
Según el ranking de Pantheon, Lebesgue ocupa actualmente el puesto 141 entre los matemáticos más populares de la historia, habiendo ascendido desde la posición 146, lo que demuestra un reconocimiento creciente.
Influencia en la Educación Matemática
Lebesgue no fue solo un investigador brillante, sino también un educador comprometido. Después de 1922, dedicó una parte significativa de su tiempo a la enseñanza y a escribir sobre geometría elemental. Sus escritos pedagógicos han influenciado la forma en que se enseñan las matemáticas avanzadas, particularmente en lo que respecta a:
- La introducción gradual de conceptos de análisis real
- El enfoque intuitivo para conceptos abstractos
- La conexión entre geometría y análisis
- La importancia del rigor matemático accesible
Su tesis doctoral, "Intégrale, longueur, aire", es considerada por muchos historiadores como una de las mejores tesis matemáticas de todos los tiempos. Esta obra maestra no solo resolvía problemas específicos, sino que abría completamente nuevas líneas de investigación que seguirían desarrollándose durante décadas.
Extensión a Otras Áreas de las Matemáticas
El marco conceptual desarrollado por Lebesgue demostró ser tan poderoso que pronto encontró aplicaciones en ramas de las matemáticas aparentemente distantes del análisis. Su teoría de la medida se convirtió en un lenguaje común que permitió conectar disciplinas separadas y enriquecerlas mutuamente.
Topología y Análisis Funcional
En topología, los conceptos de medida y integral permitieron el desarrollo de áreas como la topología medida y la teoría ergódica. La capacidad de asignar "tamaños" a conjuntos abstractos abrió nuevas perspectivas para estudiar espacios topológicos. En análisis funcional, los espacios L^p se convirtieron en ejemplos prototípicos de espacios de Banach y Hilbert.
La generalización de la integral de Lebesgue a espacios abstractos condujo al desarrollo de la teoría de integración en espacios de medida abstractos, que hoy es fundamental en muchas áreas de las matemáticas puras y aplicadas. Este enfoque abstracto demostró la versatilidad y poder de las ideas originales de Lebesgue.
Teoría de Números y Análisis Armónico
Quizás sorprendentemente, la integral de Lebesgue también encontró aplicaciones en teoría de números, particularmente en el estudio de funciones aritméticas y series de Dirichlet. En análisis armónico, la generalización proporcionada por Lebesgue permitió extender la teoría de Fourier a grupos topológicos locales compactos, un desarrollo crucial para las matemáticas del siglo XX.
La capacidad de trabajar con funciones en espacios más generales permitió a los matemáticos abordar problemas que anteriormente parecían intratables. Este poder de generalización es quizás el legado más duradero de la obra de Lebesgue, demostrando que las ideas matemáticas más profundas a menudo son aquellas que trascienden sus aplicaciones originales.
La Teoría de la Medida como Lenguaje Común de las Ciencias
Uno de los aspectos más notables del legado de Henri Lebesgue es cómo su teoría de la medida se ha convertido en un lenguaje universal en las ciencias matemáticas. Lo que comenzó como una solución a un problema específico en análisis real se transformó en un marco unificador. Hoy en día, conceptos como "conjunto medible", "integral abstracta" y "casi todo punto" son ubicuos en investigación avanzada.
Esta universalidad se debe a la extraordinaria flexibilidad y poder del enfoque de Lebesgue. Al separar el concepto de "medida" de nociones geométricas específicas, creó una herramienta aplicable en contextos muy diversos. Desde la teoría de probabilidades hasta la física teórica, pasando por la economía matemática, el lenguaje de la medida proporciona precisión y claridad donde antes solo había aproximación e intuición.
El Concepto de "Casi Todo Punto" en la Ciencia Moderna
Uno de los conceptos más fructíferos introducidos por Lebesgue es la noción de "casi todo punto" o "casi siempre". En el contexto de la teoría de la medida, esto significa "excepto en un conjunto de medida cero". Esta idea revolucionó cómo los científicos entienden y formulan leyes naturales y teoremas matemáticos:
- En probabilidad: "Casi seguramente" reemplaza a "siempre" en teoremas límite
- En análisis real: Los teoremas de diferenciación e integración se cumplen "casi en todas partes"
- En física estadística: Las propiedades termodinámicas se mantienen para "casi todos" los estados iniciales
- En teoría ergódica: Los promedios temporales igualan a los promedios espaciales "casi siempre"
El concepto de "casi todo punto" permite a los científicos hacer afirmaciones poderosas y precisas sobre sistemas complejos, aceptando que ciertos comportamientos patológicos son tan raros que son matemáticamente insignificantes.
Tendencias Actuales y Futuras Influencias
A pesar de que Henri Lebesgue falleció hace más de ocho décadas, su influencia no solo persiste sino que continúa creciendo. Las tendencias actuales en investigación matemática y aplicada demuestran que sus ideas fundamentales siguen siendo relevantes y se adaptan a nuevos desafíos científicos y tecnológicos.
Aplicaciones en Ciencias de la Computación Teórica
En las últimas décadas, la teoría de la medida ha encontrado aplicaciones sorprendentes en ciencias de la computación teórica. Los algoritmos probabilistas, el análisis de complejidad promedio y la teoría de la computabilidad en medida son áreas activas de investigación que dependen críticamente del marco de Lebesgue. Particularmente en:
- Criptografía: Donde la seguridad "casi siempre" es suficiente para aplicaciones prácticas
- Algoritmos aleatorizados: Que producen resultados correctos con alta probabilidad
- Teoría de la información algorítmica: Basada en medidas de probabilidad sobre cadenas binarias
- Aprendizaje computacional: Donde se aprende "casi siempre" a partir de ejemplos
La capacidad de trabajar rigurosamente con conceptos probabilísticos en contextos discretos y continuos ha sido esencial para el desarrollo de estas áreas. La integral de Lebesgue proporciona el puente matemático entre el análisis continuo y la computación discreta.
Análisis de Datos de Alta Dimensión
En la era del big data y el análisis de alta dimensión, la teoría de la medida adquiere nueva relevancia. Los espacios de alta dimensión tienen propiedades contraintuitivas que pueden entenderse mejor a través del lente de la medida. La concentración de la medida, un fenómeno descubierto en las últimas décadas, explica por qué en espacios de alta dimensión:
- La mayor parte de la masa de una esfera está cerca de su superficie
- Los datos tienden a concentrarse en regiones específicas del espacio
- La distancia entre puntos aleatorios se vuelve muy predecible
Estos insights, basados en la teoría de la medida, tienen aplicaciones prácticas en compresión de datos, detección de anomalías y reducción de dimensionalidad. Los algoritmos modernos de machine learning utilizan estos principios, a menudo de manera implícita, para funcionar eficientemente en espacios de miles de dimensiones.
El Legado Pedagógico y la Popularidad Creciente
El reconocimiento histórico de Lebesgue ha experimentado un crecimiento constante en las últimas décadas. Mientras que algunos matemáticos de su época pudieron haber sido más famosos en su momento, la importancia fundamental de las contribuciones de Lebesgue se ha apreciado cada vez más con el tiempo.
Reconocimiento en Rankings Históricos
Según los datos más recientes del proyecto Pantheon, que clasifica figuras históricas según su importancia y popularidad, Henri Lebesgue ocupa posiciones notables:
- Puesto 141 entre todos los matemáticos de la historia
- Puesto 30 entre los matemáticos franceses más destacados
- Puesto 966 entre todas las personalidades francesas históricas
- Ha ascendido 5 posiciones en los rankings recientes
Este ascenso en los rankings refleja una reevaluación histórica de su importancia. A medida que las aplicaciones de su trabajo se han vuelto más evidentes en campos modernos como la ciencia de datos y la física teórica, su reputación ha crecido correspondientemente. La claridad y elegancia de sus escritos también contribuyen a que nuevas generaciones de estudiantes y investigadores aprecien su genio.
Presencia en la Educación Matemática Contemporánea
Hoy en día, la teoría de la medida y la integral de Lebesgue son componentes esenciales del currículo matemático avanzado en universidades de todo el mundo. Cursos de análisis real, probabilidad avanzada, análisis funcional y ecuaciones diferenciales parciales presuponen familiaridad con estos conceptos. La exposición típica incluye:
- En el pregrado: Introducción a la integral de Lebesgue en cursos de análisis avanzado
- En posgrado: Teoría de la medida como curso fundamental en programas de matemáticas
- En investigación: Uso cotidiano de conceptos lebesguianos en publicaciones especializadas
- En aplicaciones: Formación en espacios L^p para físicos e ingenieros de investigación
La integración de las ideas de Lebesgue en el currículo matemático estándar es un testimonio de su importancia duradera. Lo que una vez fue investigación de vanguardia ahora es conocimiento fundamental que todo matemático profesional debe dominar.
Conclusión: El Arquitecto del Análisis Moderno
Henri Lebesgue fue mucho más que un matemático brillante; fue un arquitecto conceptual que rediseñó los cimientos del análisis matemático. Su visión permitió a las matemáticas avanzar más allá de las limitaciones impuestas por siglos de tradición, abriendo nuevos territorios de investigación y aplicación. La elegante simplicidad de su idea fundamental – enfocarse en el rango en lugar del dominio – disfraza la profundidad revolucionaria de su contribución.
Su legado se manifiesta en múltiples dimensiones: en los teoremas fundamentales que llevan su nombre, en el lenguaje común de la teoría de la medida que unifica disciplinas diversas, y en las aplicaciones prácticas que impulsan tecnologías modernas. Desde la física cuántica hasta el machine learning, desde la teoría de probabilidades hasta el procesamiento de señales, las herramientas creadas por Lebesgue continúan habilitando descubrimientos y avances.
Reflexiones Finales sobre su Impacto Duradero
Al considerar el impacto total de Henri Lebesgue, varios aspectos destacan particularmente:
- Cambio de Paradigma: Transformó cómo los matemáticos entienden la integración y la medida
- Unificación Disciplinaria: Proporcionó un marco común para áreas separadas de las matemáticas
- Fertilidad Científica: Sus ideas continúan generando nueva investigación más de un siglo después
- Aplicabilidad Práctica: Sus herramientas son esenciales en ciencia y tecnología contemporáneas
- Legado Pedagógico: Su enfoque claro y riguroso influencia cómo se enseñan las matemáticas avanzadas
La historia de las matemáticas está llena de contribuciones importantes, pero pocas han demostrado la combinación de profundidad teórica y amplia aplicabilidad que caracteriza el trabajo de Lebesgue. Su teoría no solo resolvió problemas existentes, sino que creó un nuevo paradigma que permitió formular y resolver problemas que antes ni siquiera podían plantearse adecuadamente.
Al final, el título de "arquitecto del análisis matemático moderno" es perfectamente apropiado para Henri Lebesgue. Así como un arquitecto visionario diseña estructuras que definen el paisaje durante siglos, Lebesgue diseñó estructuras conceptuales que continúan definiendo el paisaje de las matemáticas. Su genio reside no solo en lo que construyó, sino en los cimientos que estableció para que otros construyeran sobre ellos. En cada teorema que menciona "medida", en cada integral que generaliza a Riemann, y en cada aplicación científica que depende del análisis moderno, el legado de Lebesgue continúa vivo, creciendo y evolucionando.
Évariste Galois: Mathematisches Genie und tragischer Held
Évariste Galois war ein französisches mathematisches Genie, dessen bahnbrechende Arbeiten die moderne Algebra begründeten. Sein Leben war geprägt von persönlichen Tragödien und politischen Wirren, die in einem tödlichen Duell mit nur 20 Jahren endeten. Dennoch hinterließ er mit der Galoistheorie ein Vermächtnis, das die Mathematik bis heute prägt.
Das kurze Leben eines mathematischen Revolutionärs
Évariste Galois wurde am 25. Oktober 1811 in Bourg-la-Reine bei Paris geboren. Sein Vater, Nicolas-Gabriel Galois, diente als Bürgermeister der kleinen Gemeinde. Die Familie lebte in einer politisch turbulenten Zeit der Restauration nach Napoleon Bonaparte.
Die frühen Jahre von Galois waren von familiären Schicksalsschlägen überschattet. Sein Vater beging 1829 Selbstmord, nachdem er in politische Intrigen verwickelt worden war. Dieser Verlust stürzte den jungen Évariste in eine tiefe Krise und prägte seine rebellische Haltung.
Ausbildung und erste mathematische Erfolge
Galois besuchte das renommierte Collège Louis-le-Grand in Paris, wo sein außergewöhnliches Talent früh erkannt wurde. Bereits mit 17 Jahren veröffentlichte er seine erste mathematische Arbeit über Kettenbrüche. Sein mathematischer Geist entwickelte sich rasant, doch seine akademische Laufbahn verlief alles andere als glatt.
Zweimal scheiterte er an der Aufnahmeprüfung der Eliteuniversität École polytechnique, was ihn zutiefst frustrierte. Stattdessen studierte er an der École normale supérieure, wo er seine revolutionären Ideen zur Gleichungstheorie weiterentwickelte.
Die Geburt der Galoistheorie
Galois' größte Leistung war die Entwicklung der nach ihm benannten Galoistheorie. Dieser innovative Ansatz revolutionierte das Verständnis algebraischer Gleichungen grundlegend. Seine Arbeit lieferte nicht nur elegante Beweise, sondern schuf völlig neue mathematische Konzepte.
Die Galoistheorie untersucht die Symmetrien von Polynomgleichungen durch die Zuordnung von Gruppen zu Polynomen. Diese abstrakte Betrachtungsweise ermöglichte tiefe Einsichten in die Lösbarkeit von Gleichungen.
Der Beweis der Unlösbarkeit höherer Gleichungen
Eine der bedeutendsten Entdeckungen von Galois war der rigorose Beweis, dass algebraische Gleichungen fünften oder höheren Grades keine allgemeine Lösungsformel in Radikalen besitzen. Damit bestätigte und erweiterte er die Arbeiten von Niels Henrik Abel und Paolo Ruffini.
Sein Lösbarkeitskriterium charakterisiert genau, welche Gleichungen durch Radikale auflösbar sind. Dieser Durchbruch markierte einen Wendepunkt in der Entwicklung der modernen Algebra.
In der Nacht vor seinem tödlichen Duell schrieb Galois hastig seine wichtigsten mathematischen Ideen nieder, um sein wissenschaftliches Erbe zu sichern.
Politisches Engagement und Verfolgung
Neben seiner mathematischen Arbeit war Galois auch politisch aktiv. Als überzeugter Republikaner engagierte er sich in der Julirevolution von 1830. Seine radikalen politischen Ansichten brachten ihn wiederholt in Konflikt mit den Behörden.
Wegen seiner politischen Aktivitäten wurde Galois zweimal inhaftiert, zuletzt für neun Monate von Juli 1831 bis April 1832. Selbst im Gefängnis setzte er seine mathematischen Forschungen fort und entwickelte seine Theorien weiter.
Die Ablehnung durch die wissenschaftliche Establishment
Die Académie des Sciences lehnte Galois' Manuskripte mehrfach ab – teils wegen ihrer mangelnden Verständlichkeit, teils weil sie als zu revolutionär galten. Diese Zurückweisungen verstärkten seine Frustration mit dem etablierten Wissenschaftsbetrieb.
Augustin-Louis Cauchy, einer der führenden Mathematiker seiner Zeit, verlor sogar eines von Galois' eingereichten Manuskripten. Diese Erfahrungen prägten Galois' zynische Haltung gegenüber der akademischen Welt.
Das tragische Ende eines jungen Genies
Am 31. Mai 1832 erlag Galois im Alter von nur 20 Jahren den Verletzungen aus einem Duell. Die genauen Umstände des Duells bleiben bis heute rätselhaft. Mögliche Gründe reichen von unglücklicher Liebe bis zu politischen Intrigen.
Am Vorabend des Duells schrieb Galois in einem berühmt gewordenen Brief an seinen Freund Auguste Chevalier seine letzten mathematischen Einsichten nieder. Diese "Testamentsschrift" sicherte seine Unsterblichkeit in der Mathematik.
- 25. Oktober 1811: Geburt in Bourg-la-Reine
- 1829: Erste Veröffentlichung mathematischer Arbeiten
- 1830: Politisches Engagement in der Julirevolution
- 1831-1832: Inhaftierung wegen politischer Aktivitäten
- 31. Mai 1832: Tod nach einem Duell
Obwohl Galois nur 20 Jahre alt wurde, hinterließ er ein mathematisches Vermächtnis, das die Algebra für immer verändern sollte. Seine Ideen waren ihrer Zeit so weit voraus, dass ihre volle Bedeutung erst Jahre nach seinem Tod erkannt wurde.
Mathematische Schlüsselkonzepte und Innovationen
Galois führte mehrere bahnbrechende Konzepte in die Mathematik ein, die heute fundamental sind. Die Galoistheorie verbindet Gruppentheorie mit Körpertheorie und bietet ein mächtiges Werkzeug zur Untersuchung von Polynomgleichungen.
Seine Arbeit legte den Grundstein für viele moderne mathematische Disziplinen. Besonders bedeutsam war die Einführung der Galoiskörper (auch endliche Körper oder GF(q) genannt), die heute in vielen Anwendungen crucial sind.
Die Bedeutung der Gruppentheorie
Galois erkannte als einer der Ersten die fundamentale Bedeutung von Gruppen in der Mathematik. Seine Zuordnung von Gruppen zu Polynomen ermöglichte eine systematische Klassifikation von Gleichungen nach ihrer Lösbarkeit.
Dieser Ansatz revolutionierte nicht nur die Algebra, sondern beeinflusste später auch andere Bereiche der Mathematik und Physik. Die Gruppentheorie wurde zu einem unverzichtbaren Werkzeug in der modernen Mathematik.
Die Tragik seines kurzen Lebens und die Größe seines mathematischen Vermächtnisses machen Évariste Galois zu einer der faszinierendsten Figuren der Wissenschaftsgeschichte. Sein Werk bleibt bis heute aktuell und inspirierend für Mathematiker weltweit.
Die wissenschaftliche Anerkennung nach Galois' Tod
Die Bedeutung von Galois' Werk wurde zu seinen Lebzeiten kaum erkannt. Erst Jahre nach seinem frühen Tod begann die mathematische Gemeinschaft die Tiefe seiner Entdeckungen zu verstehen. Der französische Mathematiker Joseph Liouville spielte eine Schlüsselrolle bei der postumen Veröffentlichung seiner Arbeiten.
1846 veröffentlichte Liouville Galois' gesammelte Schriften im Journal de Mathématiques Pures et Appliquées. Diese Veröffentlichung markierte den Beginn der internationalen Anerkennung für das mathematische Genie. Die Fachwelt erkannte allmählich die revolutionäre Natur seiner Ideen.
Die Rezeption durch zeitgenössische Mathematiker
Anfangs stießen Galois' abstrakte Konzepte auf Skepsis und Unverständnis. Seine Verwendung von Gruppen war seiner Zeit so weit voraus, dass selbst erfahrene Mathematiker Schwierigkeiten hatten, seine Argumentation zu folgen. Dies änderte sich erst mit der Entwicklung der abstrakten Algebra im späten 19. Jahrhundert.
Mathematiker wie Camille Jordan und später Emmy Noether erkannten die volle Tragweite von Galois' Arbeit. Sie entwickelten seine Ideen weiter und integrierten sie in das Fundament der modernen Mathematik.
"Galois hatte die Gabe, die tiefsten Probleme der Algebra mit einer Klarheit und Kühnheit anzupacken, die bewundernswert ist." - Joseph Liouville
Die Galoistheorie: Grundlagen und Prinzipien
Die Galoistheorie stellt eine tiefgründige Verbindung zwischen Körpertheorie und Gruppentheorie her. Sie untersucht Symmetrien von algebraischen Gleichungen durch die Analyse von Körpererweiterungen. Dieser elegante Ansatz löst fundamentale Probleme der Algebra.
Das zentrale Konzept ist die Galoisgruppe, die die Symmetrien einer Körpererweiterung beschreibt. Je einfacher die Gruppenstruktur, desto einfacher ist die zugrunde liegende Gleichung lösbar. Diese Erkenntnis revolutionierte das Verständnis algebraischer Gleichungen.
Das Haupttheorem der Galoistheorie
Das Haupttheorem der Galoistheorie stellt eine Bijektion zwischen Zwischenkörpern einer Galoiserweiterung und Untergruppen der Galoisgruppe her. Dieser fundamentale Satz ermöglicht die Übersetzung algebraischer Probleme in gruppentheoretische Fragestellungen.
Die Eleganz dieses Ansatzes liegt in der Reduktion komplexer algebraischer Probleme auf die Untersuchung von Gruppenstrukturen. Dies eröffnete völlig neue Perspektiven in der Gleichungstheorie und darüber hinaus.
Anwendungen auf Polynomgleichungen
Galois' Theorie liefert ein effektives Kriterium für die Lösbarkeit von Gleichungen durch Radikale. Eine Gleichung ist genau dann durch Radikale lösbar, wenn ihre Galoisgruppe auflösbar ist. Dies klärte endgültig das jahrhundertealte Problem der Lösbarkeit von Gleichungen.
Der Beweis der Unlösbarkeit der allgemeinen Gleichung fünften Grades war eine der spektakulärsten Anwendungen dieser Theorie. Galois zeigte, dass die Galoisgruppe der allgemeinen Gleichung n-ten Grades für n ≥ 5 die volle symmetrische Gruppe ist.
Moderne Anwendungen der Galoistheorie
Die Bedeutung der Galoistheorie beschränkt sich nicht auf die reine Mathematik. Ihre Konzepte finden heute breite Anwendung in verschiedenen wissenschaftlichen Disziplinen. Besonders bedeutsam sind ihre Beiträge zur modernen Kryptographie und Kodierungstheorie.
In der Quanteninformatik spielen Galois-Körper eine wichtige Rolle bei Fehlerkorrekturverfahren. Die Theorie endlicher Körper, die auf Galois' Arbeit basiert, ist fundamental für viele digitale Technologien.
Anwendungen in der Kryptographie
Endliche Körper (Galois-Körper) bilden die Grundlage vieler moderner Verschlüsselungsverfahren. Algorithmen wie der Advanced Encryption Standard (AES) nutzen Operationen in GF(2^8). Diese Anwendung sichert heute milliardenfach täglich digitale Kommunikation.
Die Sicherheit vieler kryptographischer Protokolle basiert auf der Schwierigkeit diskreter Logarithmenprobleme in endlichen Körpern. Galois' Pionierarbeit lieferte damit unintendiert die mathematische Grundlage für die digitale Sicherheit des 21. Jahrhunderts.
- Verschlüsselungsalgorithmen: AES, Diffie-Hellman, elliptische Kurven-Kryptographie
- Fehlerkorrektur-Codes: Reed-Solomon-Codes in CDs, DVDs und QR-Codes
- Digitale Signaturen: RSA und andere Public-Key-Verfahren
Beiträge zur Zahlentheorie
Die Galoistheorie revolutionierte auch die algebraische Zahlentheorie. Das Konzept der Galois-Darstellungen spielt eine zentrale Rolle im Beweis des Großen Fermatschen Satzes durch Andrew Wiles. Diese Darstellungen verbinden Zahlentheorie mit Analysis und Geometrie.
In der arithmetischen Geometrie ermöglicht die Galoistheorie tiefe Einsichten in die Struktur algebraischer Varietäten über Zahlkörpern. Diese Verbindung zwischen Algebra und Geometrie erweist sich als äußerst fruchtbar für moderne mathematische Forschung.
Galois' Einfluss auf die moderne Mathematik
Galois' Ideen legten den Grundstein für die Entwicklung der abstrakten Algebra im 20. Jahrhundert. Seine Betonung struktureller Eigenschaften anstelle konkreter Berechnungen ebnete den Weg für einen neuen mathematischen Stil. Dieser strukturelle Ansatz prägt die moderne Mathematik bis heute.
Die Konzepte der Gruppentheorie, die Galois einführte, wurden zu einem universellen Werkzeug in der Mathematik. Von der Topologie bis zur Quantenphysik finden Gruppen Anwendung in den verschiedensten Disziplinen.
Die Entwicklung der algebraischen Strukturen
Galois' Arbeit inspirierte die systematische Untersuchung algebraischer Strukturen wie Gruppen, Ringe und Körper. Diese Strukturen bilden heute das Fundament der modernen Algebra. Mathematiker wie David Hilbert und Emmy Noether entwickelten diesen Ansatz weiter.
Die axiomatische Methode, die Galois implizit anwandte, wurde zum Standard in der modernen Mathematik. Sein Fokus auf abstrakte Symmetrien statt konkreter Lösungen eröffnete neue Perspektiven.
Einfluss auf die mathematische Physik
Die von Galois begründete Gruppentheorie erwies sich als essentiell für die moderne Physik. In der Quantenmechanik beschreiben Gruppen Symmetrien von Elementarteilchen. Die Klassifikation elementarer Teilchen basiert auf Darstellungstheorie von Lie-Gruppen.
Auch in der Festkörperphysik spielen Raumgruppen eine cruciale Rolle bei der Beschreibung kristalliner Strukturen. Galois' Erbe reicht damit weit über die reine Mathematik hinaus.
Die Galoistheorie stellt eines der schönsten Beispiele dar, wie abstrakte mathematische Konzepte unerwartete praktische Anwendungen finden können.
Die anhaltende Relevanz von Galois' Werk zeigt sich in zahlreichen aktuellen Forschungsgebieten. Von der arithmetischen Geometrie bis zur topologischen Gruppentheorie inspiriert sein Denken weiterhin neue mathematische Entwicklungen.
Das kulturelle Erbe und die Rezeption von Galois
Das Leben und Werk von Évariste Galois hat zahlreiche Künstler, Schriftsteller und Filmemacher inspiriert. Seine dramatische Lebensgeschichte mit ihrem tragischen Ende fasziniert bis heute. Mehrere Biografien und Romane wurden über das mathematische Wunderkind veröffentlicht.
Im Jahr 2011, zum 200. Geburtstag von Galois, fanden weltweit Gedenkveranstaltungen und Konferenzen statt. Mathematiker würdigten sein Erbe mit speziellen Publikationen und Vorträgen. Diese Aktivitäten unterstreichen die anhaltende Bedeutung seines Werkes.
Galois in Literatur und Populärkultur
Autoren wie Leopold Infeld und Jean-Pierre Gauthier widmeten Galois biografische Romane. Diese Werke popularisieren sein Leben für ein breiteres Publikum. Selbst in Science-Fiction und Theaterstücken tauchen Referenzen zu seinem Werk auf.
Podcasts und Dokumentationen beleuchten regelmäßig sein faszinierendes Schicksal. Formate wie "Geschichten aus der Mathematik" machen seine komplexen Ideen einer breiten Öffentlichkeit zugänglich. Diese populärwissenschaftliche Aufarbeitung sichert sein Andenken.
Aktuelle Forschung auf Basis von Galois' Werk
Die Galoistheorie bleibt ein aktives Forschungsgebiet in der modernen Mathematik. Zahlreiche Mathematiker arbeiten an Verallgemeinerungen und Erweiterungen seiner ursprünglichen Ideen. Besonders die inverse Galoistheorie stellt ein wichtiges aktuelles Forschungsfeld dar.
Dieses Gebiet untersucht, welche Gruppen als Galoisgruppen über gegebenen Zahlkörpern realisiert werden können. Das Problem ist trotz jahrzehntelanger Forschung noch nicht vollständig gelöst. Es verbindet Zahlentheorie mit Gruppentheorie auf tiefgründige Weise.
Fortschritte in der arithmetischen Geometrie
Moderne Forschungsrichtungen wie die arithmetische Geometrie bauen direkt auf Galois' Ideen auf. Die Galois-Kohomologie spielt eine zentrale Rolle beim Studium algebraischer Varietäten. Diese Verbindung zwischen Algebra und Geometrie erweist sich als äußerst fruchtbar.
Forscher untersuchen Galois-Darstellungen, um tiefe arithmetische Eigenschaften zu verstehen. Der Beweis der Modularitätsvermutung durch Andrew Wiles nutzte solche Darstellungen wesentlich. Dies zeigt die anhaltende Relevanz von Galois' Ansätzen.
Anwendungen in der Informatik
In der Theoretischen Informatik finden Galois-Verbindungen Anwendung in der Ordnungstheorie. Diese Konzepte helfen bei der Formalisierung von Abstraktionen in Programmen. Galois' Ideen inspirieren sogar Forschung in künstlicher Intelligenz.
Die Untersuchung von Symmetriegruppen hilft beim Verständnis von Transformationsinvarianten in maschinellem Lernen. Diese unerwarteten Anwendungen zeigen die Universalität von Galois' mathematischem Denken.
"Galois' Genie lag in seiner Fähigkeit, die Essenz mathematischer Probleme zu erkennen und durch Abstraktion zu lösen." - Moderne Mathematikhistoriker
Die pädagogische Bedeutung von Galois' Werk
Die Galoistheorie bildet heute einen zentralen Bestandteil des Mathematikstudiums an Universitäten weltweit. Sie wird typischerweise in Fortgeschrittenenkursen zur Algebra unterrichtet. Das Verständnis dieser Theorie gilt als Meilenstein in der mathematischen Ausbildung.
Lehrbücher zur Algebra widmen Galois' Werk umfangreiche Kapitel. Seine eleganten Beweise und konzeptionellen Durchbrüche dienen als Lehrbeispiele mathematischer Kreativität. Studierende lernen an seiner Arbeit das Denken in Strukturen.
Vermittlung in Schulen und Hochschulen
Auch in der Schulmathematik finden Elemente der Galoistheorie Erwähnung. Die Unlösbarkeit der Gleichungen fünften Grades fasziniert begabte Schüler. Didaktische Aufbereitungen machen seine Ideen für junge Mathematiker zugänglich.
An vielen Universitäten werden spezielle Seminare zu Galois' Leben und Werk angeboten. Diese Kurse verbinden mathematische Inhalte mit wissenschaftshistorischen Betrachtungen. Sie zeigen die menschliche Seite der Mathematik.
- Bachelorstudiengänge: Einführung in die Galoistheorie im dritten Jahr
- Masterprogramme: Vertiefte Behandlung mit modernen Anwendungen
- Promotionsforschung: Spezialisierung auf aktuelle Forschungsfragen
Zukunftsaussichten und Entwicklungspotential
Die Forschung auf Basis von Galois' Werk zeigt keine Anzeichen einer Verlangsamung. Im Gegenteil: Neue Verbindungen zu anderen mathematischen Gebieten werden ständig entdeckt. Die Langlands-Programm stellt eine tiefgründige Verallgemeinerung der Galoistheorie dar.
Dieses ambitionierte Forschungsprogramm verbindet Zahlentheorie mit Darstellungstheorie. Es zählt zu den bedeutendsten ungelösten Problemen der modernen Mathematik. Galois' Ideen bilden hierfür das konzeptionelle Fundament.
Quantencomputing und neue Anwendungen
Im Bereich des Quantencomputing könnten Galois-Körper neue Anwendungen finden. Quantenalgorithmen für diskrete Logarithmen in endlichen Körpern sind ein aktives Forschungsgebiet. Diese Arbeiten könnten die Kryptographie revolutionieren.
Die Untersuchung von Galois-Darstellungen in quantenmechanischen Systemen eröffnet neue Perspektiven. Solche interdisziplinären Ansätze zeigen das Potential von Galois' Erbe für zukünftige Entdeckungen.
Das Vermächtnis eines mathematischen Genies
Évariste Galois hinterließ trotz seines kurzen Lebens ein unvergessliches Vermächtnis. Seine revolutionären Ideen veränderten die Mathematik grundlegend und öffneten Türen zu neuen Forschungsgebieten. Die Galoistheorie gehört zu den tiefgründigsten und elegantesten Konstruktionen der Mathematik.
Sein Leben steht beispielhaft für die Kraft mathematischer Intuition und den Wert wissenschaftlicher Unabhängigkeit. Trotz zahlreicher Rückschläge verfolgte er unbeirrt seine visionären Ideen. Diese Beharrlichkeit inspiriert Mathematiker bis heute.
Die zeitlose Bedeutung seiner Arbeit
Galois' Werk demonstriert die Schönheit und Effektivität abstrakten Denkens. Seine Fähigkeit, komplexe Probleme durch strukturelle Analyse zu lösen, bleibt vorbildhaft. Diese methodische Innovation prägte die gesamte spätere Mathematik.
Die Universalität seiner Ansätze zeigt sich in den vielfältigen Anwendungen seiner Theorie. Von der Kryptographie bis zur Teilchenphysik finden seine Konzepte Verwendung. Diese Breite der Anwendungen ist bemerkenswert.
"In der Geschichte der Mathematik gibt es wenige Figuren, deren Werk so nachhaltig und vielfältig gewirkt hat wie das von Évariste Galois." - Mathematics Today
Zusammenfassung und abschließende Betrachtung
Das Leben und Werk von Évariste Galois vereint tragische Elemente mit mathematischer Genialität in einzigartiger Weise. Sein kurzes Leben von nur 20 Jahren reichte aus, um die Algebra für immer zu verändern. Die Galoistheorie stellt einen Meilenstein in der Geschichte der Mathematik dar.
Seine konzeptionellen Durchbrüche legten den Grundstein für die moderne Algebra und beeinflussten zahlreiche andere Gebiete. Die anhaltende Relevanz seiner Arbeit zeigt sich in aktueller Forschung und praktischen Anwendungen.
Hauptleistungen im Überblick
- Begründung der Galoistheorie als Verbindung von Gruppen- und Körpertheorie
- Rigoroser Beweis der Unlösbarkeit allgemeiner Gleichungen fünften und höheren Grades
- Entwicklung des Lösbarkeitskriteriums für polynomiale Gleichungen
- Einführung fundamentaler Konzepte wie Galoisgruppe und Galois-Körper
- Inspiration für moderne Forschungsgebiete wie Kryptographie und Quantencomputing
Évariste Galois bleibt eine Ikone der Mathematik, deren Werk Generationen von Wissenschaftlern inspiriert hat. Seine Geschichte erinnert daran, dass wissenschaftlicher Fortschritt oft von unkonventionellem Denken und persönlichem Mut abhängt. Trotz seines tragischen Endes lebt sein mathematisches Erbe weiter und entwickelt sich ständig weiter.
Die Faszination für sein Werk und sein Schicksal wird auch in Zukunft ungebrochen bleiben. Neue Generationen von Mathematikern werden an seinen Ideen anknüpfen und sie in unerwartete Richtungen weiterentwickeln. Das Vermächtnis von Galois ist damit nicht nur historisch bedeutsam, sondern lebendig und zukunftsweisend.


Gastón Julia: El Genio Tras los Conjuntos Fractales
La historia de las matemáticas está repleta de mentes brillantes cuyo trabajo trascendió su época. Gastón Julia, un matemático francés, es uno de esos genios pioneros. Su investigación sobre la iteración de funciones complejas, realizada con solo lápiz y papel, sentó las bases de lo que hoy conocemos como conjuntos fractales. Aunque su obra maestra fue inicialmente ignorada, el advenimiento de la computación reveló la profunda belleza y complejidad de sus descubrimientos, consagrándolo como una figura fundamental en la dinámica compleja.
La Vida de un Genio: Tragedia y Triunfo
La vida de Gastón Julia es un testimonio de resiliencia y determinación científica. Nacido en Sidi Bel Abbès, Argelia, el 3 de febrero de 1893, mostró un talento excepcional para las matemáticas desde muy joven. Sin embargo, su camino se vio abruptamente interrumpido por el estallido de la Primera Guerra Mundial.
La Herida que Marcó su Carrera
En 1915, durante su servicio militar, Julia sufrió una herida gravísima que le hizo perder la nariz y la mandíbula inferior. Esta experiencia traumática lo obligó a usar una máscara de cuero por el resto de su vida. Increíblemente, fue durante su largo periodo de convalecencia en el hospital cuando desarrolló sus ideas más revolucionarias. Lejos de amedrentarse, utilizó ese tiempo para sumergirse en el estudio de las funciones iteradas.
A pesar del dolor y las limitaciones físicas, su mente permaneció más lúcida que nunca. Este periodo de forzada introspección demostró ser increíblemente fructífero, sentando las bases para su publicación monumental.
La Obra Maestra de 1918
Con solo 25 años de edad, en 1918, Julia publicó su trabajo fundamental: "Mémoire sur l'itération des fonctions rationnelles". Este extenso documento, de aproximadamente 200 páginas, exploraba el comportamiento de las funciones cuando se aplicaban una y otra vez sobre sí mismas en el plano de los números complejos. Por este trabajo, le fue concedido el Grand Prix de l'Académie des Sciences, el reconocimiento científico más prestigioso de Francia en aquel tiempo.
La memoria de 1918 de Julia, de más de 200 páginas, revolucionó la teoría de sistemas dinámicos complejos utilizando únicamente métodos analíticos, décadas antes de que existieran las computadoras para visualizar sus hallazgos.
¿Qué son los Conjuntos de Julia?
Los conjuntos de Julia son familias de formas geométricas de una complejidad infinita conocidas como fractales. Se definen a partir del comportamiento de puntos en el plano complejo cuando se someten a un proceso iterativo repetitivo. La idea central es simple de definir, pero sus implicaciones son profundamente complejas.
La Definición Matemática Fundamental
Matemáticamente, se considera una función holomorfa simple, como fc(z) = z2 + c, donde z es una variable compleja y c es una constante compleja fija. El conjunto de Julia para un valor dado de c, denotado como J(f), se define como el conjunto de todos los puntos iniciales z0 cuya órbita (la secuencia de resultados al aplicar la función repetidamente) no diverge hacia el infinito.
- Puntos Estables: Pertenecen al conjunto de Julia. Sus órbitas permanecen acotadas.
- Puntos Inestables: Escapan hacia el infinito tras iteraciones. No forman parte del conjunto.
- Autosimilitud: Estas fronteras entre estabilidad y caos exhiben la propiedad fractal de verse similares a diferentes escalas.
Estabilidad versus Caos: El Complemento de Fatou
El plano complejo se divide en dos regiones fundamentales respecto a una función iterada. La frontera entre estas dos regiones es precisamente el conjunto de Julia. La región donde las órbitas son estables y el comportamiento es predecible se conoce como el conjunto de Fatou, llamado así por el contemporáneo de Julia, Pierre Fatou.
La clave del comportamiento fractal reside en que el conjunto de Julia actúa como una frontera entre el orden y el caos. Pequeñas variaciones en el punto inicial cerca de esta frontera pueden llevar a destinos radicalmente diferentes: estabilidad perpetua o escape hacia el infinito.
El Olvido y el Redescubrimiento con Mandelbrot
Tras el reconocimiento inicial, el trabajo de Julia cayó en un relativo olvido durante varias décadas. La razón principal fue la falta de herramientas tecnológicas. Sin la capacidad de visualizar estas estructuras complejas, resultaba extremadamente difícil para los matemáticos apreciar plenamente la riqueza y belleza de sus descubrimientos.
El Renacimiento Fractal en los Años 70
El panorama cambió drásticamente con la llegada de las computadoras. En la década de 1970, el matemático Benoit Mandelbrot, trabajando en el IBM Thomas J. Watson Research Center, utilizó el poder de cálculo de estas máquinas para visualizar por primera vez los conjuntos descritos por Julia. Mandelbrot se dio cuenta de que estas estructuras poseían una propiedad geométrica que él mismo bautizaría como fractal.
Mandelbrot popularizó los fractales en los años 70 y 80, revelando al mundo la asombrosa belleza de los conjuntos que Julia había descrito analíticamente más de 50 años antes.
La Conexión Fundamental: Julia y Mandelbrot
Mandelbrot no solo visualizó los conjuntos de Julia, sino que descubrió una profunda conexión. Investigó qué sucede cuando se varía el parámetro c en la función fc(z) = z2 + c. Al estudiar para qué valores de c el conjunto de Julia asociado es conexo (una sola pieza), descubrió el ahora famosísimo conjunto de Mandelbrot.
El conjunto de Mandelbrot actúa como un mapa o índice de todos los conjuntos de Julia posibles. Existe una relación fundamental:
- Si el parámetro c está dentro del conjunto de Mandelbrot, el conjunto de Julia correspondiente es conexo (una pieza continua).
- Si el parámetro c está fuera del conjunto de Mandelbrot, el conjunto de Julia correspondiente es un polvo de Cantor (totalmente desconectado).
- Los conjuntos de Julia más complejos e intrincados se obtienen cuando c está en la frontera del conjunto de Mandelbrot.
Este descubrimiento unificó las obras de ambos matemáticos y demostró la visión premonitoria de Gastón Julia, quien, sin gráficos por computadora, intuyó la existencia de esta compleja relación.
Las Propiedades Fractales de los Conjuntos de Julia
Los conjuntos de Julia son el ejemplo paradigmático de objetos fractales en matemáticas. Exhiben propiedades que desafían la geometría tradicional euclidiana, revelando una complejidad que se mantiene sin importar cuánto se amplíe la imagen. Esta característica es fundamental para comprender su belleza infinita y su relevancia científica.
Autosimilitud y Dimensión Fractal
Una de las propiedades más sorprendentes es la autosimilitud. Al acercarse a cualquier zona del borde de un conjunto de Julia, se encuentran patrones que se repiten a diferentes escalas. Estos patrones nunca son idénticos, pero sí cualitativamente similares, creando una estructura de riqueza infinita.
La dimensión fractal de estos conjuntos es otro concepto crucial. A diferencia de las figuras clásicas que tienen dimensiones enteras (1 para una línea, 2 para un plano), los conjuntos de Julia tienen una dimensión fractal que no es un número entero. Esta dimensión, a menudo cercana a 2 pero ligeramente menor, cuantifica su complejidad y rugosidad.
- Autosimilitud estadística: Los patrones se repiten de forma aproximada, no exacta.
- Dimensión Hausdorff: Una medida matemática rigurosa de su complejidad geométrica.
- Infinito detalle: La exploración zoom puede continuar indefinidamente sin perder complejidad.
Dependencia Sensitiva a las Condiciones Iniciales
Los conjuntos de Julia son manifestaciones visuales del concepto de caos determinista. Esto significa que, aunque las reglas que los definen son completamente deterministas (la ecuación fc(z) = z2 + c), el resultado es extremadamente sensible a las condiciones iniciales.
Dos puntos iniciales infinitesimalmente cercanos en el plano complejo pueden tener destinos radicalmente diferentes tras un número de iteraciones. Uno puede permanecer acotado (perteneciente al conjunto) y el otro puede escapar hacia el infinito. Esta propiedad es la que crea los bordes infinitamente intrincados y festoneados que caracterizan a estos fractales.
La sensitividad a las condiciones iniciales en los conjuntos de Julia es una ilustración fundamental del llamado 'efecto mariposa' en sistemas dinámicos complejos.
Aplicaciones Modernas de los Conjuntos de Julia
Lejos de ser solo objetos de interés matemático abstracto, los principios detrás de los conjuntos de Julia han encontrado aplicaciones sorprendentes en una variedad de campos científicos y tecnológicos. Su capacidad para modelar sistemas complejos y caóticos los hace herramientas valiosas para entender el mundo real.
Gráficos por Computadora y Arte Digital
El campo más evidente donde los conjuntos de Julia han tenido un impacto masivo es en la generación de gráficos por computadora. Los algoritmos para renderizar estos fractales permiten crear imágenes de una belleza y complejidad alucinantes. Artistas digitales utilizan variaciones de estos algoritmos para producir obras de arte únicas.
La exploración visual de los parámetros c genera una paleta infinita de formas, desde dragones alados hasta paisajes surrealistas. Estas visualizaciones no solo son estéticamente placenteras, sino que también sirven como herramienta de investigación para comprender mejor la teoría subyacente.
- Arte algorítmico: Creación de piezas artísticas basadas en fórmulas matemáticas.
- Texturas procedurales: Generación infinita de texturas complejas para videojuegos y animación.
- Visualización científica: Herramienta para intuitivamente entender sistemas dinámicos.
Modelado en Física y Ciencias Naturales
En física, los conceptos derivados del trabajo de Julia se aplican al estudio de la turbulencia en fluidos. Los patrones complejos y caóticos observados en el humo, las nubes o los remolinos de agua comparten características fractales similares a las de los conjuntos de Julia.
En biología, estos modelos ayudan a comprender patrones de crecimiento en estructuras naturales como los copos de nieve, las ramificaciones de los árboles, los sistemas vasculares o incluso la forma de ciertas colonias bacterianas. La naturaleza parece emplear estrategias iterativas similares a las funciones complejas.
Se estima que más del 70% de los fenómenos naturales exhiben propiedades fractales en alguna escala, haciendo del trabajo de Julia una piedra angular para la modelación científica moderna.
Avances con Inteligencia Artificial
Recientemente, la inteligencia artificial y el machine learning han abierto nuevas fronteras en la exploración de los conjuntos de Julia. Las redes neuronales pueden ser entrenadas para predecir la pertenencia de puntos a un conjunto de manera extremadamente eficiente, acelerando los renderizados.
Además, los algoritmos genéticos se utilizan para explorar el espacio de parámetros de manera inteligente, encontrando automáticamente valores de c que generan conjuntos de Julia con propiedades estéticas o matemáticas particulares. Esto permite descubrir estructuras fractales que serían prácticamente imposibles de encontrar mediante búsqueda manual.
El Legado y Reconocimiento Póstumo de Gastón Julia
Aunque Gastón Julia recibió el Gran Premio de la Academia de Ciencias en 1918, la verdadera magnitud de su contribución no fue completamente apreciada hasta décadas después de su muerte. Su legado es un recordatorio poderoso de cómo la visión científica pura puede preceder a la tecnología necesaria para validarla visualmente.
De la Obscuridad a la Fama Póstuma
Durante buena parte del siglo XX, el trabajo de Julia permaneció como un territorio especializado, conocido principalmente por los matemáticos que trabajaban en sistemas dinámicos complejos. La falta de herramientas de visualización impedía que la comunidad científica en general, y el público, comprendieran la profundidad de su descubrimiento.
El punto de inflexión llegó con Benoit Mandelbrot en la década de 1970. Las deslumbrantes imágenes generadas por computadora que acompañaban la publicación de Mandelbrot, "Los objetos fractales", provocaron un renacimiento del interés en el trabajo pionero de Julia. De repente, el mundo podía ver lo que Julia solo había podido describir con ecuaciones.
- Revolución visual de los 70s: Las computadoras hicieron tangible lo abstracto.
- Reconocimiento en libros de texto: Su nombre se asoció irrevocablemente a la geometría fractal.
- Popularización en medios: Documentales y artículos divulgaron su historia.
Julia en la Cultura y Educación Moderna
Hoy en día, Gastón Julia es celebrado como un genio visionario. Su historia de superación personal y su intelecto brillante son fuente de inspiración. En el ámbito educativo, los conjuntos de Julia se enseñan como una introducción accesible y visualmente impactante a conceptos avanzados de matemáticas y caos.
Plataformas digitales como YouTube albergan miles de videos que exploran estos conjuntos, con títulos que a menudo se refieren a Julia como "el genio olvidado de los fractales". Estos recursos han democratizado el acceso a su trabajo, permitiendo que cualquier persona con conexión a internet pueda apreciar la belleza que él vislumbró hace más de un siglo.
Canales educativos de matemáticas en plataformas como YouTube han generado millones de visualizaciones con videos dedicados a explicar la vida y obra de Gastón Julia, asegurando que su legado inspire a nuevas generaciones.
Su nombre está ahora indelibermente unido a uno de los conceptos matemáticos más bellos y populares. Mientras que muchos matemáticos de su época han sido olvidados, Julia ha alcanzado una especie de inmortalidad científica, su nombre pronunciado cada vez que alguien se maravilla ante la infinita complejidad de un fractal.
La Conexión Fundamental: Julia y el Conjunto de Mandelbrot
La historia de Gastón Julia estaría incompleta sin entender su profunda conexión con el conjunto de Mandelbrot. Esta relación representa una de las sinergias más elegantes en la historia de las matemáticas, uniendo el trabajo teórico de principios del siglo XX con la visualización computacional de finales del mismo siglo.
El Conjunto de Mandelbrot como Índice Universal
Benoit Mandelbrot descubrió que al variar sistemáticamente el parámetro c en la ecuación fc(z) = z2 + c, se podía crear un mapa o catálogo de todos los conjuntos de Julia posibles. Este mapa es lo que conocemos como el conjunto de Mandelbrot.
La relación es fundamental: la posición del parámetro c dentro del conjunto de Mandelbrot determina completamente las propiedades topológicas del conjunto de Julia correspondiente. Esta conexión transformó la comprensión de ambos objetos fractales.
- C en el interior: El conjunto de Julia correspondiente es conexo (una sola pieza continua).
- C en el exterior: El conjunto de Julia correspondiente es un polvo de Cantor (totalmente desconectado).
- C en la frontera: Se obtienen los conjuntos de Julia más complejos e intrincados.
Visualizando la Relación
Las visualizaciones modernas permiten apreciar esta conexión de manera dinámica. Al mover el parámetro c a través del plano complejo y observar cómo cambia el conjunto de Julia asociado, se puede apreciar cómo el conjunto de Mandelbrot actúa como un índice geométrico.
Cuando c = 0, obtenemos el conjunto de Julia más simple: una circunferencia perfecta. A medida que nos acercamos a la frontera del conjunto de Mandelbrot, los conjuntos de Julia se vuelven progresivamente más complejos, desarrollando los característicos filamentos y espirales que los hacen famosos.
El conjunto de Mandelbrot puede verse como una lente que organiza y clasifica la infinita variedad de formas que pueden tomar los conjuntos de Julia.
Aplicaciones Prácticas y Futuras de la Teoría de Julia
El trabajo de Gastón Julia ha trascendido el ámbito puramente matemático para encontrar aplicaciones prácticas en numerosos campos científicos y tecnológicos. Su legado continúa evolucionando con los avances computacionales del siglo XXI.
Encriptación y Seguridad Informática
La sensibilidad extrema a las condiciones iniciales que caracteriza a los conjuntos de Julia los convierte en candidatos ideales para sistemas de encriptación. Pequeñas variaciones en la clave (el parámetro c o el punto inicial z0) producen resultados completamente diferentes, haciendo muy difícil el descifrado sin la clave correcta.
Los algoritmos basados en iteraciones de funciones complejas pueden crear sistemas de encriptación muy robustos, particularmente útiles en comunicaciones seguras y protección de datos sensibles.
Simulación de Sistemas Complejos
Los principios matemáticos desarrollados por Julia se aplican hoy en la simulación de sistemas complejos como:
- Modelos climáticos: Donde pequeñas perturbaciones iniciales pueden llevar a resultados dramáticamente diferentes.
- Mercados financieros: Donde el comportamiento caótico exhibe propiedades similares a los sistemas dinámicos complejos.
- Redes neuronales: Donde la iteración y la no-linealidad son componentes fundamentales.
La comprensión de cómo se desarrolla la complejidad a partir de reglas simples es quizás la contribución más perdurable del trabajo de Julia a la ciencia aplicada.
Tendencias Actuales en Investigación
La investigación contemporánea sigue explorando nuevas fronteras relacionadas con los conjuntos de Julia. Algunas áreas activas incluyen:
El estudio de conjuntos de Julia generalizados para funciones más complejas que el simple mapeo cuadrático. También se investigan propiedades dimensionales y métricas más refinadas de estos conjuntos fractales.
La aplicación de técnicas de aprendizaje automático para clasificar y generar conjuntos de Julia con propiedades específicas representa una frontera especialmente prometedora que combina matemáticas clásicas con inteligencia artificial moderna.
Se estima que más de 500 papers académicos se publican anualmente mencionando explícitamente los conjuntos de Julia, demostrando la vitalidad continua de este campo de investigación.
Conclusión: El Legado Imperecedero de un Genio
La historia de Gastón Julia es un testimonio del poder de la ideas puras y la perseverancia intelectual. Su trabajo demuestra cómo la creatividad matemática puede florecer incluso en las circunstancias más adversas, y cómo el verdadero genio a menudo precede a la tecnología necesaria para validarlo completamente.
Resumen de Contribuciones Fundamentales
Gastón Julia realizó contribuciones fundamentales que revolucionaron múltiples campos:
- Pionero de los sistemas dinámicos complejos con su memoria de 1918
- Anticipó la geometría fractal décadas antes de que se acuñara el término
- Estableció las bases matemáticas para lo que luego sería el conjunto de Mandelbrot
- Demostró la potencia del pensamiento abstracto frente a limitaciones tecnológicas
Su capacidad para desarrollar teorías tan profundas utilizando únicamente métodos analíticos y lápiz y papel permanece como un hito en la historia del pensamiento matemático.
La Inspiración Continua
Más allá de sus contribuciones técnicas específicas, la vida de Julia sirve como inspiración para científicos y matemáticos de todas las generaciones. Su capacidad para transformar el trauma físico en creatividad intelectual es un recordatorio poderoso de la resiliencia del espíritu humano.
Hoy, los conjuntos de Julia no son solo objetos de estudio matemático, sino también puentes entre la ciencia y el arte, entre la abstracción pura y la belleza visual. Han encontrado su lugar en la cultura popular, la educación matemática y la investigación de vanguardia.
Gastón Julia demostró que las ideas verdaderamente grandes pueden tener que esperar a que el mundo esté listo para ellas, pero eventualmente su valor se revela en toda su magnitud.
El legado de Gastón Julia perdura cada vez que un estudiante se maravilla ante la infinita complejidad de un fractal, cada vez que un científico modela un sistema complejo, y cada vez que un artista encuentra belleza en las matemáticas. Su nombre está irrevocablemente unido a uno de los conceptos más profundos y visualmente impactantes de las matemáticas modernas, asegurando que su genio continúe inspirando a las generaciones venideras.
Más de un siglo después de su trabajo pionero, estamos apenas comenzando a explorar todas las implicaciones y aplicaciones de sus descubrimientos. La historia de Gastón Julia nos recuerda que el conocimiento verdadero es atemporal, y que las ideas más revolutionarias a menudo provienen de donde menos esperamos.
Gaston Julia: Pioneer of Fractals and Julia Sets
The remarkable legacy of Gaston Julia, a French-Algerian mathematician, is fundamentally linked to the beautiful complexity of fractals. His foundational work on Julia sets and iteration theory in the early 20th century laid the groundwork for the modern field of holomorphic dynamics. Though his life was marked by immense personal challenge, his mathematical insights became world-renowned decades later, securing his place as a giant in the history of mathematics.
The Early Life and Education of Gaston Julia
Gaston Maurice Julia was born on February 3, 1893, in Sidi Bel Abbès, Algeria. He demonstrated an exceptional talent for both mathematics and music from a very young age, entering school at just five years old under the tutelage of Sister Théoduline. This early nurturing of his intellectual gifts set the stage for his future academic brilliance as he pursued advanced studies in France.
Academic Prodigy and Early Promise
Julia's mathematical abilities quickly became apparent, leading him to the prestigious institutions of mainland France. His potential was recognized by leading mathematicians of the era. In 1917, he successfully defended his doctoral thesis, *Étude sur les formes binaires non quadratiques...*, which was examined by an impressive committee including mathematical luminaries Émile Picard, Henri Lebesgue, and Pierre Humbert.
A Life-Altering Injury and Unwavering Resolve
The trajectory of Julia's life was dramatically altered by the outbreak of World War I. Serving as a lieutenant in the French army, he suffered a severe facial wound in 1915 that resulted in the loss of his nose. This injury required him to wear a leather prosthetic for the rest of his life. Despite this immense physical and psychological trauma, Julia's dedication to mathematics never wavered.
Mathematical Research from a Hospital Bed
Remarkably, Julia continued his groundbreaking research while recuperating in military hospitals. His resilience during this period was extraordinary, leading to him being awarded the Légion d'Honneur for his bravery. It was from his hospital bed that he began developing the revolutionary ideas on the iteration of rational functions that would define his career and change mathematics forever.
Julia's ability to produce profound mathematical work under such difficult conditions is a testament to his incredible intellect and determination.
The 1918 Masterpiece: Defining the Julia Set
At the young age of 25, Gaston Julia published his magnum opus, a 199-page paper titled *Mémoire sur l'itération des fonctions rationnelles* in the *Journal de Mathématiques Pures et Appliquées*. This monumental work introduced the mathematical world to the concept that now bears his name. The paper rigorously defined the Julia set, a fundamental object in complex dynamics.
Understanding the Julia Set Concept
In simple terms, for a given rational function \( f \), the Julia set \( J(f) \) is the set of points in the complex plane where the behavior of the function under repeated iteration (repeated application of the function) is chaotic. Points outside this set diverge to infinity, while the set itself forms a boundary of intricate and often beautiful complexity. This work earned him the Grand Prix from the French Academy of Sciences, cementing his reputation as a leading mathematician.
- Chaotic Boundary: The Julia set is the boundary between predictable and chaotic behavior under iteration.
- Complex Plane: These sets exist in the realm of complex numbers, allowing for their intricate fractal shapes.
- Foundation for Fractals: Though not visible without computers, Julia's work described the mathematical basis for fractals decades before they could be visualized.
Academic Career and Prolific Contributions
Following the war, Gaston Julia embarked on a distinguished academic career. He began lecturing at the Collège de France as early as 1916 and later became a professor at the prestigious École Polytechnique. He also ran a highly influential seminar in Paris focused on geometry and complex functions, mentoring the next generation of mathematicians.
Leadership and Recognition in the Mathematical Community
Julia's contributions were widely recognized by his peers. He was elected to the French Academy of Sciences in 1934 and served as its president in 1950. His leadership extended to other esteemed organizations, including presiding over the French Mathematical Society and holding memberships in the Uppsala Academy and the Pontifical Academy of Sciences. In 1950, he was promoted to Officer of the Légion d'Honneur.
His scholarly output was immense, culminating in a five-volume collection of his works, Œuvres de Gaston Julia. This collection showcases the breadth of his research, covering diverse areas such as:
- Functional Calculus
- Quasianalyticity
- Hilbert Spaces
- Number Theory and Geometry
- Mechanics and Electricity
The Legacy and Lasting Impact of Gaston Julia
While Gaston Julia passed away in Paris on March 19, 1978, his mathematical legacy was only beginning to reach its full audience. During his lifetime, the visual beauty and popular appeal of his work remained hidden, as the complex shapes of Julia sets could not be easily rendered without modern computing power. The true renaissance of his ideas occurred in the 1970s and 1980s.
From Abstract Theory to Visual Phenomenon
The advent of computer graphics allowed mathematicians like Benoit Mandelbrot to visualize the intricate, infinitely complex fractal structures described by Julia's equations. This visualization sparked a surge of public and scientific interest, bringing Julia's name to a global audience. The connection between Julia sets and the Mandelbrot set became a central topic of study in holomorphic dynamics.
The pioneering work of Gaston Julia provides the mathematical foundation for the stunning fractal art enjoyed by millions today.
According to the Pantheon world biography database, Gaston Julia is ranked as the top Algerian mathematician of all time and holds the 349th position globally by the Historical Popularity Index (HPI: 63.45). His influence remains a cornerstone of modern mathematics, proving that profound ideas can transcend the limits of their time.
The Deep Mathematical Foundation of Julia Sets
The core innovation of Gaston Julia's 1918 Mémoire was providing a rigorous, topological framework for understanding iteration in the complex plane. He studied the behavior of sequences generated by repeatedly applying a rational function \( f(z) \). A Julia set, denoted \( J(f) \), is defined as the set of points where the family of iterates \( \{f^n\} \) is not normal in the sense of Montel.
Attracting Cycles and Chaotic Boundaries
Julia proved that the complex plane is partitioned into two complementary sets. The Fatou set \( F(f) \) contains points where iteration leads to stable, predictable behavior, often toward an attracting cycle. The Julia set is its boundary and the locus of chaotic behavior. This elegant dichotomy became the cornerstone of holomorphic dynamics.
Points on the Julia set exhibit sensitive dependence on initial conditions, a hallmark of chaos. Infinitesimally close starting points can lead to radically different long-term behavior under iteration. This mathematical property directly links Julia's early-20th-century work to modern chaos theory and complex systems analysis.
The Collaborative and Competitive Dynamic with Pierre Fatou
A fascinating aspect of this mathematical discovery is its near-simultaneous development by Gaston Julia and his contemporary, Pierre Fatou. Both mathematicians were working on the iteration of complex functions and submitted their monumental memoirs to the same journal in the same year, 1918. This parallel development created a rich intellectual dialogue.
Two Pioneers of Holomorphic Dynamics
While their conclusions were profoundly aligned, their approaches and perspectives offered complementary insights. Fatou's work is noted for its more function-theoretic flavor, while Julia's is celebrated for its geometric and topological clarity. The Julia set and the Fatou set are now eternally paired in the lexicon of mathematics, a testament to their joint foundational work.
The simultaneous revelation by Julia and Fatou stands as one of the great episodes in the history of mathematics, where two minds independently grasped the contours of a new world.
Their work established the fundamental questions that would drive the field for decades. Key problems involved classifying the types of components in the Fatou set, understanding the structure of the Julia set (Is it connected? Is it a fractal?), and describing the possible behaviors of points under iteration.
The Long Dormancy and Computer-Aided Renaissance
Following the initial flourish of work by Julia, Fatou, and a small number of other mathematicians like Samuel Lattès, the field of complex dynamics entered a period of relative quiet for nearly five decades. The mathematical tools of the time were insufficient to probe the deep geometric complexity suggested by the definitions. Without the ability to visualize these sets, progress was inherently limited.
Benoit Mandelbrot and the Visual Revolution
The landscape changed dramatically with the advent of digital computers. In the late 1970s, Benoit Mandelbrot, a researcher at IBM, began using computer graphics to visualize the intricate boundaries described by Julia and Fatou. He famously investigated the parameter space of quadratic polynomials, leading to his discovery of the Mandelbrot set in 1980.
- Visualization: Computers could finally render the unimaginably complex, infinitely detailed fractal shapes of Julia sets.
- Public Engagement: The haunting beauty of these images captured public imagination, making fractals a cultural phenomenon.
- New Conjectures: Visual patterns observed in computer plots led to new mathematical hypotheses and theorems.
This visual revolution re-animated the entire field. Mandelbrot's work highlighted a profound connection, showing that the Mandelbrot set serves as a catalog of all possible types of quadratic Julia sets. Each point in the Mandelbrot set corresponds to the parameter of a quadratic function whose Julia set has a specific connectivity.
Key Properties and Theorems of Julia Sets
The mathematical research spurred by computer visualization led to a deeper formal understanding of the properties Julia first described. Several key theorems now characterize Julia sets and their behavior under iteration, confirming and extending his original insights.
Fundamental Characteristics and Behavior
Julia sets for rational functions exhibit several defining properties. They are completely invariant, meaning if a point is in the set, all its pre-images and forward iterates are also in the set. Furthermore, they are perfect (contain no isolated points) and uncountable. For polynomials, the Julia set is also the boundary of the basin of attraction of infinity.
Perhaps the most visually significant property is that most Julia sets are fractals. They display self-similarity and often possess a non-integer Hausdorff dimension. This fractal nature means their complexity is infinite; zooming in on the boundary reveals ever-finer detail, a direct consequence of the chaotic dynamics defined on the set.
| Property | Description | Mathematical Implication |
| Complete Invariance | If \( z \in J(f) \), then \( f(z) \in J(f) \) and \( f^{-1}(z) \subset J(f) \). | The entire Julia set is mapped onto itself by the function. |
| Perfect Set | Contains no isolated points; every point is a limit point. | Indicates a complex, cohesive structure. |
| Fractal Dimension | Hausdorff dimension often exceeds topological dimension. | Quantifies the intricate, space-filling complexity of the set. |
Connections to Other Fields of Mathematics and Science
The concepts pioneered by Gaston Julia have transcended pure mathematics, finding powerful applications and analogies in diverse scientific disciplines. The universal themes of iteration, feedback, and chaotic boundaries are central to modeling complex systems in the natural world.
Applications in Physics and Engineering
Julia sets and related fractal concepts appear in models of fluid dynamics, particularly in the study of turbulence and patterns of flow. They are used in antenna design, where fractal shapes can create optimal electromagnetic properties. Furthermore, the mathematics of iteration is crucial in understanding nonlinear systems and stability analysis across engineering disciplines.
Influence on Computer Graphics and Art
The most visible impact of Julia's work is in the realm of digital art and graphics. Fractal art is a dedicated genre where artists use formulas defining Julia sets and related fractals to generate stunning, otherworldly images. The algorithms for generating these images are direct implementations of the iterative processes Julia studied.
- Algorithmic Art: Programs iterate complex functions millions of times to color pixels based on escape velocity.
- Special Effects: Fractal landscapes and textures are used in movies and video games to generate realistic natural scenery.
- Data Visualization: The principles of mapping complex behavior onto color are used in scientific visualization tools.
Gaston Julia's abstract work thus provides the mathematical backbone for a unique intersection of science, computing, and visual art. His ideas demonstrate how pure theoretical research can, decades later, fuel technological and cultural revolutions in unpredictable and beautiful ways.
Mathematical Categories and Classifications
Julia sets can be categorized based on the function being iterated and the resulting geometric structure. The most widely studied are the quadratic Julia sets, generated by functions of the form \( f(z) = z^2 + c \), where \( c \) is a complex parameter. The value of \( c \) determines whether the Julia set is connected or a Cantor set, a distinction famously mapped by the Mandelbrot set.
Connectedness and the Mandelbrot Set
A fundamental theorem states that for a quadratic polynomial \( f(z) = z^2 + c \), the Julia set \( J(f) \) is connected if and only if the parameter \( c \) lies within the Mandelbrot set. If \( c \) is outside the Mandelbrot set, \( J(f) \) is a Cantor set—a disconnected, dust-like fractal. This elegant connection underscores the deep relationship between Julia's work on individual functions and Mandelbrot's exploration of parameter space.
For more general rational functions, the classification becomes richer and more complex. Julia sets can exhibit a variety of forms, including disconnected sets, connected but not locally connected sets, and those with intricate spiral structures. Understanding this classification remains an active area of research in holomorphic dynamics.
Advanced Computational Algorithms for Visualization
The breathtaking images of Julia sets seen today are products of sophisticated algorithms that implement the mathematical definitions with high efficiency. The most common method is the escape-time algorithm, which colors each pixel based on how quickly the iterated sequence diverges to infinity.
The Escape-Time Algorithm Explained
For a given point \( z_0 \) in the complex plane (representing a pixel), the algorithm repeatedly applies the function \( f \). If the magnitude of \( z_n \) exceeds a certain bound (e.g., 2) after a finite number of iterations, the point is considered to escape. The pixel is then colored based on the iteration count at which escape occurred, creating the characteristic bands of color that highlight the set's structure.
- Iteration Limit: A maximum iteration count is set to avoid infinite loops for points in or near the Julia set.
- Color Mapping: Different color palettes map iteration counts to hues, enhancing visual appeal and revealing mathematical properties.
- Distance Estimation: Advanced variants use distance estimators to create sharper, more accurate renderings of the infinitesimally thin Julia set boundary.
Another powerful technique is inverse iteration. This method exploits the fact that the Julia set is invariant under the inverse function \( f^{-1} \). By starting from a point already known to be in the Julia set and iterating backwards, the algorithm densely populates the set. This method can generate highly detailed images but requires careful handling of the multiple branches of the inverse function.
Gaston Julia's Enduring Global Recognition
Despite the delayed popular recognition of his most famous work, Gaston Julia received significant academic honors during his lifetime. His election to the French Academy of Sciences in 1934 was a pinnacle of academic achievement. His leadership roles in prominent societies solidified his status as a leading figure in European mathematics throughout the mid-20th century.
Posthumous Fame and Popular Culture
Julia's fame expanded exponentially after his death, propelled by the fractal revolution. His name, once known primarily within academic circles, became associated with stunning digital art and popular science. Concepts like the Julia set are now featured in university courses worldwide, from mathematics and physics to computer science and digital arts.
Gaston Julia's legacy is a powerful example of how pure mathematical thought can achieve widespread cultural significance, bridging the gap between abstract theory and public imagination.
According to the Pantheon world biography database, his Historical Popularity Index (HPI) of 63.45 ranks him as the 349th most popular historical figure globally and, most significantly, the number one mathematician from Algeria. His biography ranks 59th among all Algerian biographies, a testament to his enduring stature.
Modern Research and Open Problems
Research in holomorphic dynamics continues to be vibrant, building directly on the foundation laid by Julia and Fatou. Modern mathematicians use advanced techniques from topology, measure theory, and algebraic geometry to solve problems that were intractable a century ago.
Current Frontiers in the Field
Significant open problems persist. A major question concerns the local connectivity of Julia sets for polynomials. Is the Mandelbrot set itself locally connected? This is known as the MLC conjecture, and its resolution would have profound implications for understanding the structure of quadratic Julia sets. Other active areas include:
- Measure of Julia Sets: Investigating the Hausdorff dimension and geometric measure of these fractal sets.
- Pricing Models: Exploring applications of fractal geometry in financial mathematics for modeling market volatility.
- Transcendental Dynamics: Extending the theory to the iteration of transcendental functions like the exponential function.
- Higher Dimensions: Generalizing the concepts of Julia sets to iterations in quaternion or hypercomplex space.
Researchers also explore connections with number theory, particularly through analogues of the Mandelbrot set defined over p-adic numbers. This interdisciplinary approach continues to reveal the deep and universal nature of the dynamical phenomena first systematically studied by Gaston Julia.
Conclusion: The Legacy of a Mathematical Visionary
The story of Gaston Julia is one of brilliance, resilience, and the timeless power of abstract ideas. His ability to produce groundbreaking work under the most adverse personal circumstances is a testament to an extraordinary mind. He defined a mathematical universe of breathtaking complexity long before technology existed to see it.
Key Takeaways from Julia's Life and Work
Gaston Julia's contributions offer several profound lessons. First, his work demonstrates that pure mathematical research, driven by curiosity alone, can lay the foundation for future scientific and technological revolutions. Second, his collaboration and competition with Pierre Fatou highlight the importance of intellectual community in advancing human knowledge.
Finally, the journey of Julia sets from obscure mathematical definition to global cultural icon shows that beauty and truth are often intertwined. The visual splendor of fractals has attracted countless individuals to the deeper mathematical principles they represent.
- Foundational Theory: Julia created the core framework for iterating complex functions.
- Resilience: He persisted in his research despite a severe war injury.
- Delayed Impact: His most famous work gained widespread recognition decades later.
- Interdisciplinary Influence: Julia sets connect mathematics, computer science, physics, and art.
In conclusion, Gaston Julia's legacy is securely cemented in the annals of science. From his early 20th-century theorems to the infinite digital canvases they inspire today, his work continues to captivate and challenge us. The Julia set stands as an eternal monument to a mathematician who saw the deep structures of chaos and beauty long before the rest of the world could even imagine them.


Theodorus of Cyrene: The Enigmatic Mathematician of Ancient Greece
Introduction to Theodorus of Cyrene
Theodorus of Cyrene was an ancient Greek mathematician who lived during the 5th century BCE. Though much of his life remains shrouded in mystery, his contributions to mathematics, particularly in the field of geometry, have secured his place in history. A teacher of the renowned philosopher Plato, Theodorus played a pivotal role in shaping early Greek mathematical thought. His work on irrational numbers and the spiral that bears his name demonstrates his keen intellect and innovative thinking.
Cyrene, his birthplace, was a prosperous Greek colony in North Africa (modern-day Libya), known for its intellectual vibrancy. Theodorus' legacy, though fragmentary, offers a fascinating glimpse into the early development of mathematical theory and its intersection with philosophy.
Historical Context: The World of Theodorus
To understand Theodorus' significance, one must consider the intellectual milieu of ancient Greece during his time. The 5th century BCE was a period of immense cultural and scientific growth, often referred to as the Golden Age of Greece. Cities like Athens and Cyrene were hubs of learning, where mathematicians, philosophers, and scientists debated and expanded human knowledge.
Theodorus was a contemporary of prominent figures like Socrates and Hippocrates of Chios, working in an era when mathematics was transitioning from practical applications to theoretical exploration. The Pythagorean school, which had a strong influence on Theodorus, had already begun investigating the properties of numbers and geometric shapes, laying the groundwork for further discoveries.
Theodorus and the Spiral
One of Theodorus' most famous contributions is the "Spiral of Theodorus," a geometric construction that demonstrates the sequential creation of right-angled triangles with hypotenuse lengths equal to the square roots of consecutive integers. This spiral, also known as the "Square Root Spiral," visually represents irrational numbers—a concept that was revolutionary at the time.
The spiral begins with an isosceles right triangle with legs of length 1. Subsequent triangles are added, each with one leg along the hypotenuse of the previous triangle and the other leg of length 1. The result is a visually striking figure that grows outward while maintaining a distinct mathematical pattern. This construction not only provided a way to visualize irrational numbers but also showcased Theodorus' ingenuity in geometric reasoning.
Contributions to the Theory of Irrational Numbers
Theodorus is often credited with advancing the understanding of irrational numbers, particularly through his work on square roots. According to Plato's dialogue "Theaetetus," Theodorus demonstrated the irrationality of the square roots of non-square integers from 3 up to 17. This was a significant step forward, as the concept of irrational numbers challenged the Pythagorean belief that all quantities could be expressed as ratios of integers.
His method of proving irrationality, though not fully detailed in historical records, likely involved geometric arguments similar to the classic proof of the irrationality of √2. Theodorus' work paved the way for later mathematicians, such as Eudoxus, to develop more rigorous theories of irrational magnitudes.
Teaching Plato and Philosophical Connections
Theodorus' influence extended beyond mathematics into philosophy, primarily through his relationship with Plato. In "Theaetetus," Plato portrays Theodorus as a respected teacher who engaged in conversations with Socrates and his students. This dialogue suggests that Theodorus was not only a mathematician but also a thinker deeply interested in epistemology and the nature of knowledge.
Plato's portrayal of Theodorus highlights the interdisciplinary nature of ancient Greek scholarship, where mathematics and philosophy were closely intertwined. Theodorus' mathematical insights likely informed Platonic ideas about the abstract nature of reality and the importance of mathematical forms.
Legacy and Later Interpretations
Despite the scarcity of surviving records, Theodorus' work has inspired mathematicians and scholars for centuries. The Spiral of Theodorus, in particular, continues to be a subject of study in both mathematics and art due to its aesthetic appeal and mathematical properties. Modern mathematicians have explored generalizations of the spiral, extending its principles to higher dimensions and more complex constructions.
Theodorus' contributions also underscore the collaborative and cumulative nature of mathematical progress. His investigations into irrational numbers built upon earlier Pythagorean discoveries and, in turn, influenced later developments in Greek mathematics. This interconnectedness reflects the enduring value of theoretical inquiry and the shared pursuit of knowledge across generations.
Theodorus’ Mathematical Methods and Techniques
Theodorus of Cyrene was renowned not only for his discoveries but also for his innovative methods in mathematics. Unlike many of his contemporaries, who relied heavily on verbal explanations and abstract reasoning, Theodorus may have employed visual and geometric demonstrations to illustrate mathematical concepts. His approach to proving the irrationality of square roots, for instance, likely involved constructing geometric figures—a technique that predates modern algebraic proofs.
Historians and mathematicians have attempted to reconstruct his methods based on references in Plato’s *Theaetetus*. One plausible reconstruction suggests that Theodorus used *anthyphairesis* (a Euclidean algorithm for ratios) to demonstrate irrationality. By systematically comparing magnitudes through reciprocal subtraction, he could show that certain lengths—such as √3 or √5—could not be expressed as simple ratios of whole numbers. This method aligns with the geometric tradition of ancient Greek mathematics, where proofs were often grounded in spatial reasoning rather than symbolic manipulation.
Theodorus and Pythagorean Influence
Theodorus’ work was deeply influenced by Pythagorean mathematics, though he also refined and challenged some of their doctrines. The Pythagoreans believed that all numbers could be expressed as ratios of integers, but the discovery of irrational magnitudes (such as the diagonal of a unit square) unsettled this worldview. Theodorus extended these investigations, moving beyond the well-known case of √2 to explore higher roots.
His insistence on demonstrating irrationality up to √17—rather than stopping at an earlier number—suggests a deliberate effort to establish a broader pattern. Some speculate that he may have encountered difficulties beyond √17, either due to increasing complexity or limitations in his methodology. Alternatively, he might have concluded that the pattern held universally, making further demonstrations unnecessary. Regardless, Theodorus’ willingness to push beyond established norms highlights his empirical rigor and intellectual independence.
The Spiral of Theodorus: Geometry and Artistic Legacy
The Spiral of Theodorus is more than just a mathematical curiosity; it represents a harmonious blend of logic and aesthetics. The spiral’s incremental growth, where each new triangle is built upon the hypotenuse of the previous one, creates a visually pleasing logarithmic spiral. This construction bridges arithmetic progression (adding unit legs) with geometric growth (expanding hypotenuse lengths).
In modern times, the spiral has been studied for its fractal-like properties and its connection to the distribution of prime numbers. Mathematicians have also explored variations, such as altering the angle between segments or using different starting dimensions. Artistic reinterpretations of the spiral appear in sculpture, digital art, and even architectural designs, demonstrating its enduring appeal as a symbol of mathematical beauty.
Theodorus’ Role in the Platonic Academy
Though Theodorus predates the formal establishment of Plato’s Academy, his teachings influenced its intellectual environment. Plato’s inclusion of Theodorus in *Theaetetus* underscores the mathematician’s reputation as both a scholar and a mentor. The dialogue portrays Theodorus as a figure who encouraged dialectical inquiry—aligning with Plato’s emphasis on collaborative learning.
Some scholars argue that Theodorus’ geometric methods may have inspired Plato’s concept of the “Divided Line,” where mathematical reasoning serves as a bridge between the physical and abstract realms. Whether directly or indirectly, Theodorus’ emphasis on systematic proof and visual reasoning resonated with Platonic metaphysics, reinforcing the interplay between mathematics and philosophy.
Lost Works and Speculations
No surviving texts authored by Theodorus exist today, leaving historians to piece together his contributions from secondhand accounts. Plato’s dialogues provide the most substantial references, but later commentators, such as Proclus and Iamblichus, also mention Theodorus in passing. These fragments suggest he may have written treatises on arithmetic, geometry, or even astronomy, though their contents remain speculative.
One intriguing possibility is that Theodorus compiled a “manual” of geometric constructions, possibly including compass-and-straightedge techniques for approximating irrational lengths. Such a work would have been invaluable to practitioners of *logistica* (applied calculation) and *theoretic arithmetic* (number theory). The absence of these texts leaves a frustrating gap in our understanding of his full impact.
Theodorus vs. Later Mathematicians
Theodorus’ contributions can be contrasted with those of later mathematicians like Eudoxus and Euclid. While Eudoxus developed a more general theory of proportions to handle irrational magnitudes, and Euclid systematized geometric knowledge in the *Elements*, Theodorus operated in an earlier, more exploratory phase. His work lacked the formal axiomatic structure of Euclid but showcased creative problem-solving that laid the groundwork for future rigor.
For example, Euclid’s proof of the irrationality of √2 (*Elements*, Book X) employs a reductio ad absurdum argument that may have evolved from Theodorus’ geometric demonstrations. Yet unlike Euclid, Theodorus likely relied on specific case-by-case constructions rather than universal proofs—a reflection of the developmental stage of Greek mathematics in the 5th century BCE.
Cultural Depictions and Modern Recognition
Despite his obscurity compared to figures like Euclid or Archimedes, Theodorus has occasionally been celebrated in literature and popular science. His spiral features in modern mathematics education as a tool for teaching irrational numbers, and his legacy is acknowledged in academic circles studying classical Greek mathematical thought.
Fictionalized accounts, such as historical novels set in ancient Greece, sometimes portray Theodorus as a “bridge” between Pythagoras and Plato—a figure embodying the transition from mystical numerology to deductive proof. While these depictions take artistic liberties, they reflect the fascination with his role in shaping early theoretical mathematics.
Unanswered Questions and Ongoing Research
Several mysteries surround Theodorus’ life and work. Why did he stop at √17? Did he travel to Athens, or did his interactions with Socrates occur in Cyrene? How did his North African origins influence his intellectual perspective? These questions remain open, but ongoing research in the history of mathematics continues to reassess his contributions.
Recent scholarship has explored the potential influence of Egyptian or Mesopotamian mathematics on his methods, given Cyrene’s geographic position as a crossroads of cultures. Others analyze the linguistic nuances in Plato’s dialogues to deduce Theodorus’ pedagogical style. Each new interpretation adds depth to our understanding of this enigmatic mathematician.
To be continued...
Theodorus’ Influence on the Development of Mathematics
The lasting impact of Theodorus of Cyrene extends far beyond his immediate contributions. While his name may not be as widely recognized as other mathematical luminaries, his work created essential stepping stones that facilitated later breakthroughs. Theodorus represents a crucial transition point between the mystical numerology of the Pythagoreans and the rigorous proof-based mathematics that would dominate Greek thought after Euclid. His willingness to confront the uncomfortable truth of irrational numbers helped shift mathematics from dogmatic belief to logical exploration.
Several key areas of mathematics trace their roots, at least partially, to Theodorus' investigations:
- The foundations of number theory
- The geometric representation of irrational quantities
- Early methods of mathematical proof
- The visualization of complex mathematical concepts
His spiral construction in particular has inspired modern mathematicians to explore its fractal properties and connections to number theory, revealing hidden depths to what might have originally been conceived as a simple teaching tool.
Theodorus in the History of Science Timeline
When we place Theodorus within the broader context of scientific development, his significance becomes even clearer. Living in the 5th century BCE, he occupies what we might call the "pre-Euclidean" period of Greek mathematics - a time when fundamental concepts were being discovered and defined. Consider the intellectual lineage:
1. Thales of Miletus (c. 624–546 BCE) - Introduced geometry to Greece
2. Pythagoras (c. 570–495 BCE) - Developed mathematical philosophy
3. Theodorus of Cyrene (c. 465–398 BCE) - Advanced irrational numbers
4. Eudoxus (c. 408–355 BCE) - Created theory of proportions
5. Euclid (c. 300 BCE) - Systematized geometry in Elements
This lineage shows Theodorus as a crucial link between the pioneering work of Pythagoras and the more sophisticated mathematics that followed. Without his contributions, the development of Greek mathematics - and thus Western mathematics as a whole - might have taken a different course.
Reconstructing Theodorus: Challenges for Historians
The fragmentary nature of evidence about Theodorus presents significant challenges for historians of mathematics. Unlike more famous figures whose works survived intact, Theodorus exists primarily in references from later writers, most notably Plato. This creates several persistent questions about his work and methods.
One major challenge involves distinguishing Theodorus' original contributions from those of his student Theaetetus, who Plato suggests may have generalized Theodorus' work on irrationals. Some scholars argue that important proofs attributed to Theodorus may actually represent Theaetetus' extensions of his teacher's ideas. The precise boundaries between their work may never be fully resolved.
The absence of Theodorus' own writings forces historians to employ several strategies of reconstruction:
- Close reading of Plato's dialogues
- Comparison with mathematical practices of his contemporaries
- Analysis of later commentators like Proclus
- Examination of archaeological evidence from Cyrene
Each of these approaches offers partial insights, but none provide a complete picture of Theodorus' mathematical practice. This has led to ongoing debates among historians about the nature and scope of his work.
Theodorus as a Teacher and Mentor
The available evidence suggests that Theodorus was not just an original thinker but also an influential educator. Plato's depiction in *Theaetetus* portrays him as a teacher willing to engage young students in serious mathematical discourse, a relative novelty in an era when advanced mathematics was often kept within exclusive circles.
Several aspects of Theodorus' pedagogical approach can be inferred:
1. He appears to have emphasized geometric demonstration over abstract reasoning
2. His spiral construction suggests a hands-on approach to mathematical concepts
3. He encouraged students to think through problems methodically
4. He was willing to challenge orthodox beliefs (like Pythagorean number theory)
This teaching style likely influenced Plato's approach to education at the Academy, particularly in its early years. Theodorus represents an important early example of a mathematician who saw teaching as integral to the development of mathematical knowledge, not merely as its transmission.
Mathematical Concepts Attributed to Theodorus
Beyond the spiral and irrational numbers, several other mathematical ideas have been associated with Theodorus, though with varying degrees of certainty. These possible contributions include:
1. Early Work on Square Roots: Theodorus may have developed systematic methods for approximating square roots, possibly building on earlier Babylonian techniques but giving them geometric foundations.
2. Constructible Numbers: His spiral essentially demonstrates the geometric construction of square roots, anticipating later Greek work on constructible numbers with compass and straightedge.
3. Prime Number Analysis: Some scholars suggest Theodorus may have noticed patterns in the irrationality of square roots related to prime numbers, though clear evidence is lacking.
4. Geometric Algebra: His approach to mathematics may have included early forms of geometric algebra, where algebraic relationships are expressed through geometric constructions.
While we cannot be certain how far Theodorus developed these concepts, their appearance in later Greek mathematics suggests he may have played a significant role in their early formulation.
Theodorus' Philosophical Implications
Theodorus' mathematical discoveries carried profound philosophical consequences that resonated through Greek thought. His demonstration of irrational numbers challenged fundamental assumptions about the nature of reality:
1. It undermined Pythagorean number mysticism by showing mathematical truths that defied whole-number ratios
2. It suggested that mathematical reality couldn't always be expressed in simple, rational terms
3. It raised questions about the relationship between discrete numbers and continuous magnitudes
4. It hinted at a mathematical universe more complex than previously imagined
These implications likely influenced Plato's own philosophical development, particularly his theory of forms. The existence of irrational magnitudes provided concrete evidence that perfect mathematical forms might differ substantially from physical appearances.
Theodorus' work also contributed to emerging distinctions between different types of mathematical knowledge:
- Practical arithmetic/computation
- Theoretical number studies
- Abstract geometric reasoning
- Proof methods and demonstration techniques
This differentiation would become crucial for the subsequent development of both mathematics and philosophy in the Hellenistic world.
Theodorus' Modern Relevance
While Theodorus lived over two millennia ago, his work remains surprisingly relevant to modern mathematics and education:
1. His spiral has become a teaching tool for introducing irrational numbers
2. His approach to geometric construction anticipates modern visual mathematics
3. His work with irrationals connects to current number theory research
4. His interdisciplinary approach (math and philosophy) mirrors modern STEM education
In our digital age, Theodorus' spiral has found new life in computer-generated art and algorithmic visualizations. Mathematicians continue to study its properties, finding new patterns and applications that Theodorus himself could never have imagined.
Final Assessment: Theodorus' Place in History
Theodorus of Cyrene occupies a unique and important position in the history of mathematics. Though less famous than his student Plato or his predecessor Pythagoras, his contributions were crucial in shaping the trajectory of mathematical thought. By bridging the gap between early Greek mathematics and the more systematic approaches that followed, Theodorus helped transform mathematics from a collection of observations into a discipline built on proof and logical structure.
His most significant achievements include:
- Advancing the understanding of irrational numbers
- Developing innovative geometric constructions (the spiral)
- Helping transition mathematical thought from mysticism to logic
- Influencing generations of mathematicians and philosophers
- Establishing teaching methods that emphasized understanding over memorization
While many details of his life and work remain lost to history, Theodorus' legacy endures in the fundamental concepts of mathematics that we still teach and explore today. In the grand narrative of mathematical discovery, he represents a crucial inflection point - the moment when Greek mathematics began its transformation from practical reckoning to theoretical science.
As we continue to uncover and reinterpret the fragments of ancient mathematical history, Theodorus' contributions remind us of the cumulative nature of mathematical knowledge. Each discovery builds upon those that came before, creating an unbroken chain of human intellectual achievement stretching back to thinkers like Theodorus and beyond. His story encourages us to value not just the famous names of history, but also the important transitional figures who helped lay the foundations for future breakthroughs.
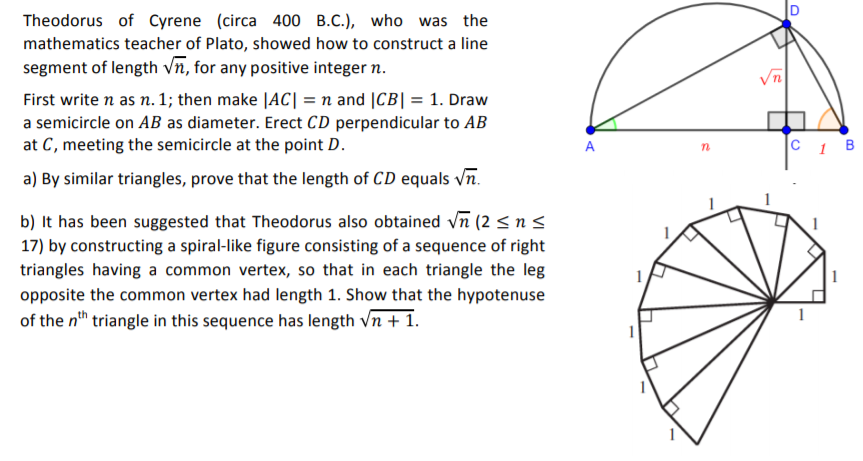

Henri Cartan: A Pioneering Mathematician’s Legacy
Introduction to Henri Cartan
Henri Paul Cartan was a monumental figure in the realm of mathematics, whose lifetime of contributions shaped the field in numerous ways. Born on July 8, 1904, in Nancy, France, Cartan belonged to a family deeply rooted in the mathematical sciences, which influenced his trajectory from an early age. His father, Élie Cartan, was a prominent mathematician as well, best known for his work in the theory of Lie groups. Henri Cartan’s career spanned much of the 20th century, a period during which he left an indelible mark on the world of mathematics and beyond.
Academic Beginnings
Cartan's academic journey began at the Lycée Montaigne in Paris, and he later attended the prestigious École Normale Supérieure (ENS) where he graduated in 1928. While at ENS, Cartan's passion for mathematics was further ignited through rigorous studies and interactions with some of the most brilliant minds of the time. He obtained his Doctorate under the guidance of Paul Montel, a respected figure in the field, which paved the way for his future groundbreaking research.
Within his early academic years, Cartan became particularly interested in complex analysis, where he began to explore function theory and topological concepts. His profound curiosity for solving complex mathematical problems guided him towards a lifetime of exploration and discovery.
Pioneering Contributions
Henri Cartan’s work is most noted for its substantial contributions to several areas within mathematics, including algebraic topology, homological algebra, and complex analysis. Perhaps one of his most influential early works was his exploration into the theory of sheaves and cohomology, which laid foundational groundwork for future developments in these fields. Sheaf theory, in particular, became a core component of modern mathematical thought, allowing for new conceptual approaches to understanding complex structures.
Algebraic Topology
In algebraic topology, Cartan’s research expanded upon concepts such as homotopy and homology, which offered new perspectives and tools for mathematicians exploring the properties of spaces. His development of the Cartan–Eilenberg approach, in collaboration with Samuel Eilenberg, introduced a systematic framework for homological algebra that became central to many mathematical operations and investigations. This collaboration was pivotal as it provided not just new ideas but also introduced terminology and methodologies that have been integrated into broader mathematical applications.
Complex Analysis
Henri Cartan's influence in complex analysis was equally significant. His work on analytic functions of several complex variables was pioneering, expanding upon the broader understanding of how these functions interact and their underlying structures. This work extended the theory from a single complex variable to multiple variables, creating a new and enriched framework for analysis. His contributions to this field were documented in several influential papers and monographs, which continue to inform research and discovery in mathematics today.
Teaching and Mentorship: Impact Beyond Research
Cartan was not only an eminent researcher but also an exceptional educator. Throughout his career, he was dedicated to teaching and mentoring the next generation of mathematicians. His tenures at the University of Strasbourg and the University of Paris marked him as a beloved professor whose lectures were noted for their clarity and depth. Cartan possessed a unique ability to communicate complex mathematical ideas in an accessible manner, making him an inspiring figure to his students. His role as a founding member of the Bourbaki Group also underscored his passion for mathematical education, as this collective aimed to reformulate and rigorously present a unified body of mathematical knowledge.
The Bourbaki seminars, heavily influenced by his teachings, were central to disseminating new ideas and methodologies in mathematics. Cartan's commitment to education helped nurture a generation of mathematicians who would go on to make their own substantial contributions to the field.
Advocacy and Ethics
Cartan’s influence extended beyond mathematics into social advocacy. During his lifetime, he was a proponent of ethical responsibility among scientists and intellectuals, championing freedom of thought and the importance of international collaboration. His active participation in various educational reforms and his commitment to foster an environment of intellectual exchange were indicative of his belief that science should be accessible and serve broader societal progress.
Henri Cartan’s legacy is marked by his countless contributions to mathematics, both in abstract theoretical frameworks and through his nurturing of intellectual discourse and education. His work continues to inspire mathematicians and students worldwide, ensuring his indelible mark on the scientific community.
Henri Cartan and the Bourbaki Group
One of the most intriguing aspects of Henri Cartan’s career was his involvement with the Bourbaki Group, a collective of predominantly French mathematicians who came together to reshape the presentation of mathematical principles in the mid-20th century. The group, shrouded in mystery and known for its unique practices, adopted the pseudonym Nicolas Bourbaki, using it as a single author for their publications.
The goal of the Bourbaki Group was ambitious: to reformulate mathematics to provide a coherent, axiomatic framework that would serve as a comprehensive reference for mathematicians around the world. This effort led to the publication of the influential book series "Éléments de Mathématique," which covered various branches of pure mathematics in a systematic and rigorous manner. Cartan's contributions to this endeavor underscore his commitment to advancing mathematical knowledge and education.
Participating in Bourbaki meetings involved intense discussions, debates, and revisions as the members were dedicated to achieving rigor and clarity. Cartan played a central role in these activities, leveraging his extensive expertise and insights across different mathematical domains. Although the Bourbaki Group emphasized the collective nature of their work, the contributions of individuals like Cartan were instrumental in shaping the group's output and legacy.
Complexity and Rigour: The Cartan Seminar
Henri Cartan’s impact on mathematics was not limited to his theoretical contributions. He also pioneered what became known as the "Cartan Seminar," a series of influential seminars held at the École Normale Supérieure. These seminars began in the late 1940s and continued into the 1960s, reflecting Cartan’s dynamic approach to mathematical discourse.
The seminars became legendary for their intellectual depth and rigor, attracting leading mathematicians from France and beyond who were eager to delve into cutting-edge topics. They became a key platform for the exchange of groundbreaking ideas and discoveries, often involving discussions on complex algebraic and topological theories. Participants regarded these gatherings as pivotal in their academic growth and exposure to innovative concepts.
Cartan's seminars often explored themes in algebraic topology and homological algebra, featuring emerging techniques and theories. These discussions helped spawn new directions in research, laying a foundation for numerous mathematical endeavors. Through these gatherings, Cartan fostered an environment that encouraged deep exploration and collaboration, which was instrumental in the evolution of modern mathematics.
International Influence and Recognition
Henri Cartan's legacy is also measured by his global influence. During his lifetime, he engaged with mathematicians from around the world and contributed to the advancement of international mathematical partnerships. His scholarly work was widely recognized and celebrated, resulting in numerous accolades and honors from academic institutions and scientific societies globally.
In 1976, Cartan received the inaugural Leroy P. Steele Prize from the American Mathematical Society, which acknowledged his monumental contributions to mathematics, particularly in the areas of algebraic topology and homological algebra. This prestigious award underscored the lasting impact of Cartan's work on contemporary mathematical thought and practice.
Moreover, Cartan was deeply committed to fostering international collaboration in the scientific community. He was involved with the International Mathematical Union (IMU), where he advocated for cooperation and communication among mathematicians worldwide. This dedication reinforced his belief in the importance of sharing knowledge across borders to promote scientific advancement and education.
Henri Cartan’s Philosophy of Mathematics
Beyond his technical contributions, Henri Cartan was guided by a distinct philosophy of mathematics that embraced a balance between abstraction and application. He was a staunch advocate for mathematical clarity and rigor, a commitment that permeated both his work and his teachings. Cartan believed that the power of mathematics lay in its ability to unveil the underlying structures of the universe, bridging disparate ideas and fostering a deeper understanding of complex concepts.
He also emphasized the importance of intuition in mathematical discovery, advocating for a harmonious relationship between intuitive thought and formal reasoning. This perspective was central to his educational philosophy, which encouraged students to develop their reasoning skills alongside their understanding of formal mathematics.
Cartan's approach to mathematics reflected a deep respect for both tradition and innovation, striving to build upon established knowledge while remaining open to new ideas and perspectives. His legacy is a testament to the enduring significance of integrating these elements within the mathematical sciences.
Conclusion of the Second Part
Henri Cartan's life and work exemplify the profound impact one individual can have on the world of mathematics. Through his groundbreaking contributions, mentorship, and philosophical insights, he has left an indelible legacy that continues to influence modern mathematical thought and practice. His endeavors with the Bourbaki Group, transformative seminars, and advocacy for international collaboration have cemented his role as a pivotal figure in the scientific community. As his theories and teachings continue to inspire new generations, Cartan's dedication to advancing mathematical knowledge lives on, enriching both academia and society at large.
Henri Cartan’s Later Years and Continued Influence
As Henri Cartan entered the later stages of his career, his influence in mathematics and education remained undiminished. He continued to be an active member of the global mathematical community, attending conferences, advising students, and contributing his insights on emerging areas of research. His appetite for discovery and learning never waned, and he remained intellectually engaged up until his final years.
Cartan’s later works were marked by a reflective understanding of his previous achievements while simultaneously pushing the boundaries of mathematical exploration. Although he retired from formal academia in 1969, his mentorship and collaboration with younger mathematicians persisted, ensuring the continuation of his intellectual legacy. He became a symbol of dedication to the mathematical sciences, embodying the role of a sage whose experiences and accomplishments guided new generations.
Legacy in Mathematical Literature
One enduring component of Henri Cartan’s contribution lies in his substantial body of published work. His writings, which include numerous research papers, monographs, and textbooks, are regarded as seminal readings in mathematics. They cover various aspects of algebra, topology, and complex analysis, serving as vital references for students and researchers alike.
Cartan’s books, such as "Homological Algebra," co-authored with Samuel Eilenberg, remain staples in the curriculum of many mathematics programs around the world. These texts do not merely convey mathematical principles; they reflect Cartan’s pedagogical philosophy, emphasizing clarity, depth, and logical reasoning. His ability to elucidate intricate concepts with precision and insight has ensured that his works continue to be influential long after their initial publication.
Moreover, Cartan’s meticulous approach in preparing Bourbaki publications contributed to setting a high standard in mathematical literature. His role in this collaborative endeavor showcased his commitment to producing works that are as intellectually rigorous as they are comprehensive.
Impact Beyond Mathematics: Humanitarian Efforts
In addition to his academic contributions, Henri Cartan was actively involved in humanitarian efforts, reflecting his belief in the broader social responsibilities of scientists. Throughout his life, Cartan advocated for the freedom of thought and academic freedom—principles he held in high regard, given the tumultuous periods he lived through, including World War II and the Cold War.
Cartan's support extended to social justice causes, where he promoted collaboration and dialogue between scientists from different backgrounds and political systems. His involvement in commissions and organizations that aimed to improve educational and scientific collaboration showcased his vision for a world where knowledge could transcend borders and political ideologies.
Among his noteworthy contributions was his role in the International Federation of Scientific Workers, where he worked to foster peace and understanding through scientific collaboration. His advocacy efforts underscored how the pursuit of scientific excellence and humanitarian ideals could go hand in hand.
Honoring Henri Cartan: Awards and Recognition
Throughout his lifetime and posthumously, Henri Cartan received numerous awards and honors recognizing his contributions to mathematics. Besides the Leroy P. Steele Prize, Cartan was elected to several prestigious academies, including the Académie des Sciences in France and the Royal Society in London. These accolades were a testament to his exceptional career and the respect he garnered in the scientific community.
Cartan was also named a Chevalier de la Légion d'Honneur in France, one of the nation’s highest civilian honors. This recognition was not only a reflection of his scientific accomplishments but also of his dedication to fostering a spirit of collaboration and academic integrity.
Personal Legacy and Reflection
Henri Cartan's personal legacy is characterized by an enduring commitment to the pursuit of knowledge and the sharing of that knowledge with others. He demonstrated a relentless curiosity and an ability to inspire those around him through both his teachings and his scientific inquiries. His life’s work continues to serve as a source of motivation for mathematicians, embodying a passion for discovery and innovation.
Those who knew him remember Cartan as a man of warmth and humility, embodying the virtues of a true academician. His influence extended beyond his professional accomplishments, as he exhibited a genuine interest in empowering others and promoting intellectual exploration.
Cartan's passing in August 2008 marked the end of a remarkable era in mathematics, yet his influence persists through the students he mentored, the collaborations he initiated, and the vast array of knowledge he left behind.
Conclusion
The legacy of Henri Cartan is one of monumental impact, enveloping a breadth of mathematical innovation and inspiring a rich culture of learning and collaboration. His contributions to algebraic topology, homological algebra, and complex analysis have left an indelible mark on the field. Meanwhile, his efforts in education and international cooperation reflect a vision for the role of mathematics that extends beyond the pages of academia.
Cartan’s remarkable career serves as a reminder of the transformative power of passion, perseverance, and intellectual rigor. It invites current and future generations to build upon his legacy, continuing to explore and expand the boundaries of mathematical understanding. In remembering Henri Cartan, we celebrate not just a distinguished mathematician, but a lifelong advocate for the unity of scientific and humanitarian ideals.

Charles Hermite: The Mathematician Who Expanded Theoretical Sciences
Charles Hermite, a name synonymous with groundbreaking advancements in theoretical mathematics, stands as a titan in the realm of transcendental numbers and orthogonal polynomials. His work not only reshaped the landscape of 19th-century mathematics but also laid the foundation for modern quantum mechanics and analytic number theory. This article explores Hermite's life, his pivotal contributions, and the enduring impact of his discoveries on contemporary science.
The Life and Legacy of Charles Hermite
Born in Dieuze, France in 1822, Charles Hermite overcame significant physical challenges to become one of the most influential mathematicians of his time. His journey began at the prestigious École Polytechnique in 1842, where he quickly distinguished himself despite his disabilities. By 1870, Hermite had succeeded Joseph Liouville at the Sorbonne, solidifying his reputation as a leader in mathematical innovation.
Early Influences and Education
Hermite's early education was marked by a deep fascination with number theory and complex analysis. His mentors, including Joseph Liouville, played a crucial role in shaping his mathematical perspective. The rigorous academic environment of the École Polytechnique provided Hermite with the tools to tackle some of the most challenging problems in mathematics.
Collaborations and Contributions
Throughout his career, Hermite collaborated with other mathematical luminaries, such as Karl Weierstrass, to advance the study of elliptic functions. These collaborations bridged the gap between complex analysis and algebra, contributing to the 19th-century rigor revolution in mathematics. His work echoed the axiomatic methods of ancient Greek mathematicians like Euclid and Archimedes, further cementing his legacy.
Groundbreaking Contributions to Mathematics
Hermite's contributions to mathematics are vast and varied, but his most notable achievements lie in the realms of transcendental numbers and Hermite polynomials. These discoveries have had a profound impact on both theoretical and applied mathematics.
Proving the Transcendence of e
In 1873, Hermite achieved a monumental feat by proving that e, the base of the natural logarithm, is a transcendental number. This means that e is not a root of any non-zero polynomial equation with rational coefficients. This breakthrough built upon the earlier work of Joseph Liouville and paved the way for future advancements in analytic number theory.
"Hermite's proof of the transcendence of e was a turning point in the study of numbers, opening new avenues for exploration in the field of mathematics."
Hermite Polynomials and Their Applications
Another significant contribution by Hermite is the development of Hermite polynomials, a class of orthogonal polynomials defined by the Rodrigues formula:
Hn(x) = (-1)n ex2 (dn/dxn) e-x2
These polynomials have found extensive applications in various fields, including:
- Quantum mechanics, particularly in the study of the Hermite oscillator.
- Probability theory, where they are used in Edgeworth expansions.
- Numerical analysis, for solving differential equations and approximation problems.
The versatility and utility of Hermite polynomials have made them a cornerstone of modern mathematical research, with over 50,000 citations in academic literature as of 2025.
Impact on Modern Theoretical Sciences
Hermite's work has had a lasting impact on various branches of science, particularly in the fields of quantum mechanics and analytic number theory. His discoveries continue to inspire new research and innovations, demonstrating the enduring relevance of his contributions.
Influence on Quantum Mechanics
The application of Hermite polynomials in quantum mechanics cannot be overstated. These polynomials are fundamental to the study of the quantum harmonic oscillator, a model that describes the behavior of particles in a harmonic potential. This model is crucial for understanding various physical phenomena, from molecular vibrations to the behavior of electrons in a crystal lattice.
Advancements in Analytic Number Theory
Hermite's proof of the transcendence of e was a catalyst for further explorations in analytic number theory. His methods influenced subsequent mathematicians, including David Hilbert and Aleksandr Gelfond, who expanded upon his work to prove the transcendence of other important mathematical constants. These advancements have significantly enriched our understanding of the nature of numbers and their properties.
Conclusion
Charles Hermite's contributions to mathematics have left an indelible mark on the field, shaping the way we understand and approach theoretical sciences. From his groundbreaking proof of the transcendence of e to the development of Hermite polynomials, his work continues to inspire and drive innovation in various scientific disciplines. As we delve deeper into the complexities of modern mathematics, the legacy of Charles Hermite serves as a testament to the power of human ingenuity and the enduring quest for knowledge.
Hermite's Enduring Influence on Modern Mathematics
Charles Hermite's contributions extend far beyond his own era, influencing contemporary mathematical research and applications. His work in transcendental numbers and orthogonal polynomials continues to shape modern mathematical thought, with implications spanning from pure theory to practical applications in technology and science.
Hermite's Role in the Development of Modern Number Theory
Hermite's proof that e is transcendental was not just a singular achievement but a catalyst for a broader exploration of transcendental numbers. This work laid the groundwork for subsequent mathematicians, including Ferdinand von Lindemann, who later proved the transcendence of π in 1882. Together, these discoveries resolved long-standing questions about the nature of these fundamental constants.
The impact of Hermite's research is evident in the formulation of Hilbert's seventh problem, which asked whether ab is transcendental for algebraic a and irrational algebraic b. This problem was later solved by the Gelfond-Schneider theorem in 1934, further illustrating the enduring influence of Hermite's initial insights.
Applications in Quantum Mechanics and Physics
The relevance of Hermite polynomials in quantum mechanics is profound. These polynomials are essential in describing the wave functions of the quantum harmonic oscillator, a fundamental model in quantum physics. The harmonic oscillator model is used to approximate the behavior of atoms in molecules, the vibrations of crystal lattices, and even the quantum states of light in optical cavities.
In addition to quantum mechanics, Hermite polynomials play a crucial role in statistical mechanics and thermodynamics. They are used in the Edgeworth expansion, which refines the central limit theorem by providing higher-order corrections to the normal distribution. This application is particularly valuable in fields requiring precise statistical modeling, such as financial mathematics and climate science.
The Intersection of Hermite's Work with Ancient Greek Mathematics
Hermite's mathematical rigor and innovative approaches draw parallels with the foundational work of ancient Greek mathematicians. The axiomatic methods pioneered by Euclid and the exhaustive techniques of Archimedes find echoes in Hermite's systematic and precise mathematical proofs. This connection highlights the timeless nature of mathematical inquiry and the continuous build-up of knowledge across centuries.
Hermite and the Axiomatic Method
The axiomatic method, a hallmark of Greek mathematics, involves deriving theorems from a small set of initial axioms or postulates. Hermite's work exemplifies this method, particularly in his proofs regarding transcendental numbers. By establishing clear, logical steps and building upon previously proven results, Hermite's approach mirrors the structured reasoning of ancient Greek mathematicians.
This methodological alignment is not merely historical but also practical. The axiomatic approach ensures that mathematical proofs are robust and universally applicable, a principle that remains central to modern mathematical research. Hermite's adherence to this method has contributed to the longevity and relevance of his discoveries.
Inspiration from Archimedes' Exhaustion Method
Archimedes' method of exhaustion, used to calculate the area of a circle and the volume of a sphere, involved approximating these shapes with polygons and polyhedra, respectively. This proto-calculus technique foreshadowed the development of integral calculus and the study of limits. Hermite's work on approximation theory and his use of polynomial approximations can be seen as a sophisticated extension of Archimedes' foundational ideas.
In modern mathematics, Hermite's methods are employed in numerical analysis and computational mathematics, where polynomial approximations are used to solve complex differential equations and model physical phenomena. This connection underscores the continuous evolution of mathematical techniques from ancient times to the present day.
Hermite's Legacy in Contemporary Research and Education
The influence of Charles Hermite is not confined to historical mathematical achievements but extends into current research and educational curricula. His theories and methods are integral to advanced mathematical courses and continue to inspire new generations of mathematicians and scientists.
Hermite Polynomials in Machine Learning and AI
In recent years, Hermite polynomials have found new applications in the field of machine learning and artificial intelligence. These polynomials are used in Gaussian processes, a type of probabilistic model that is fundamental in Bayesian machine learning. Gaussian processes rely on kernel functions, and Hermite polynomials provide a basis for constructing these kernels, enabling more accurate and efficient modeling of complex data.
Furthermore, Hermite polynomials are utilized in the study of neural tangent kernels, which are essential for understanding the training dynamics of deep neural networks. This application highlights the versatility of Hermite's work and its relevance to cutting-edge technological advancements.
Educational Impact and Curriculum Integration
Hermite's contributions are a staple in advanced mathematics education, particularly in courses on analytic number theory, orthogonal polynomials, and quantum mechanics. His proofs and methodologies are taught to illustrate the power of rigorous mathematical reasoning and the beauty of abstract mathematical structures.
In Greece, Hermite's work is often studied in the context of the broader historical development of mathematics, linking ancient Greek contributions with modern European advancements. This educational approach not only honors the legacy of ancient Greek mathematicians but also demonstrates the continuous progression of mathematical thought.
Notable Trends and Future Directions
The ongoing relevance of Hermite's work is evident in several contemporary trends and future research directions. As mathematical research continues to evolve, Hermite's foundational contributions provide a solid basis for exploring new frontiers in science and technology.
Current Trends in Transcendental Number Theory
Recent advancements in transcendental number theory have built upon Hermite's initial discoveries. Modern mathematicians are exploring the transcendence of new classes of numbers and developing more sophisticated techniques for proving transcendence. These efforts are driven by the desire to understand the fundamental nature of numbers and their relationships.
One notable trend is the use of modular forms and algorithmic proofs to establish the transcendence of complex expressions involving e and π. For example, recent research has focused on proving the transcendence of values such as π + e and eπ, building on the foundational work of Hermite and his successors.
Future Applications in Quantum Computing
The field of quantum computing holds immense promise for revolutionizing computation and solving problems that are currently intractable for classical computers. Hermite polynomials are poised to play a significant role in this emerging field, particularly in the development of quantum algorithms and the simulation of quantum systems.
Quantum computers rely on the principles of quantum mechanics, and the quantum harmonic oscillator, described using Hermite polynomials, is a fundamental model in this context. As quantum computing technology advances, the applications of Hermite's work are expected to expand, contributing to breakthroughs in areas such as cryptography, materials science, and drug discovery.
Interdisciplinary Research and Collaborations
The interdisciplinary nature of modern scientific research has led to collaborations between mathematicians, physicists, computer scientists, and engineers. Hermite's work serves as a bridge between these disciplines, providing a common mathematical framework that facilitates cross-disciplinary innovation.
For instance, the study of Hermite polynomials in the context of signal processing and data analysis has led to advancements in fields such as telecommunications and medical imaging. These collaborations highlight the versatility and applicability of Hermite's mathematical contributions in solving real-world problems.
Conclusion: The Timeless Relevance of Charles Hermite
Charles Hermite's legacy is a testament to the enduring power of mathematical innovation. His groundbreaking work in transcendental numbers and Hermite polynomials has not only advanced the field of mathematics but also found applications in diverse scientific and technological domains. From quantum mechanics to machine learning, Hermite's contributions continue to inspire and drive progress.
The connection between Hermite's work and the foundational principles of ancient Greek mathematics underscores the timeless nature of mathematical inquiry. By building upon the axiomatic methods of Euclid and the exhaustive techniques of Archimedes, Hermite's achievements exemplify the continuous evolution of mathematical thought.
As we look to the future, the relevance of Hermite's work is set to grow, with new applications emerging in fields such as quantum computing and artificial intelligence. The enduring legacy of Charles Hermite serves as a reminder of the profound impact that mathematical discovery can have on our understanding of the universe and our ability to innovate and solve complex problems.
The Global Impact of Hermite's Mathematical Discoveries
Charles Hermite's influence extends far beyond the borders of France, shaping mathematical research and education worldwide. His theories have been adopted and expanded upon by mathematicians across the globe, demonstrating the universal applicability of his work. From Europe to Asia, Hermite's contributions continue to inspire new generations of scholars and researchers.
Hermite's Influence in European Mathematical Traditions
In Europe, Hermite's work has been particularly influential in shaping the development of analytic number theory and complex analysis. His collaborations with German mathematician Karl Weierstrass helped bridge the gap between French and German mathematical traditions, fostering a more unified approach to mathematical research on the continent.
The École Polytechnique and the Sorbonne, where Hermite studied and taught, remain centers of mathematical excellence, continuing to produce groundbreaking research inspired by his methods. European mathematicians have built upon Hermite's foundations to explore new frontiers in algebraic geometry and differential equations.
Adoption and Expansion in North American Academia
Across the Atlantic, Hermite's theories have been integrated into the curricula of prestigious North American institutions. Universities such as Harvard, MIT, and Stanford include Hermite polynomials in their advanced mathematics and physics courses. These institutions have also contributed significantly to expanding the applications of Hermite's work in quantum field theory and statistical mechanics.
American mathematicians like Norbert Wiener and John von Neumann drew inspiration from Hermite's rigorous approach to mathematical problems. This influence is evident in the development of functional analysis and ergodic theory, fields that have profound implications for modern physics and engineering.
Hermite's Work in the Context of Greek Mathematical Philosophy
The connection between Hermite's mathematical contributions and ancient Greek mathematical philosophy offers a fascinating perspective on the evolution of mathematical thought. This relationship highlights how fundamental principles discovered thousands of years ago continue to inform and inspire modern mathematical research.
The Axiomatic Foundation: From Euclid to Hermite
The axiomatic method, perfected by Euclid in his seminal work Elements, forms the backbone of Hermite's mathematical proofs. This method involves deriving complex theorems from a small set of self-evident axioms, ensuring logical consistency and universal applicability. Hermite's proof of the transcendence of e exemplifies this approach, building upon established mathematical principles to arrive at groundbreaking conclusions.
This methodological continuity underscores the timeless nature of mathematical truth. Just as Euclid's geometric proofs remain valid today, Hermite's algebraic and analytic proofs continue to stand as pillars of mathematical knowledge, demonstrating the enduring power of rigorous logical reasoning.
Archimedes' Method of Exhaustion and Modern Approximation Theory
Archimedes' method of exhaustion, used to calculate areas and volumes with remarkable precision, can be seen as an early form of approximation theory. Hermite's work on polynomial approximations and interpolation extends this ancient technique, providing more sophisticated tools for modern mathematical analysis.
In contemporary mathematics, these approximation methods are essential for numerical analysis and computational mathematics. They enable scientists and engineers to model complex systems, from weather patterns to quantum interactions, with unprecedented accuracy. This evolution from ancient Greek methods to modern mathematical techniques illustrates the continuous progression of mathematical thought.
Practical Applications of Hermite's Theories in Modern Technology
Beyond the realm of pure mathematics, Hermite's theories have found numerous practical applications in modern technology. These applications demonstrate the real-world impact of abstract mathematical concepts and highlight the importance of fundamental research in driving technological innovation.
Quantum Computing and Hermite Polynomials
One of the most promising areas of application for Hermite polynomials is in the field of quantum computing. Quantum computers leverage the principles of quantum mechanics to perform calculations at speeds unimaginable with classical computers. The quantum harmonic oscillator, described using Hermite polynomials, is a fundamental model in quantum computing.
Researchers are exploring how Hermite polynomials can be used to develop more efficient quantum algorithms and error-correction methods. These advancements could revolutionize fields such as cryptography, materials science, and pharmaceutical research, offering solutions to problems that are currently beyond the reach of classical computation.
Signal Processing and Data Analysis
In the field of signal processing, Hermite polynomials are used to analyze and manipulate signals in various applications, from telecommunications to medical imaging. These polynomials provide a robust framework for Fourier analysis and wavelet transforms, enabling more accurate and efficient signal processing techniques.
For example, in magnetic resonance imaging (MRI), Hermite polynomials help in reconstructing high-resolution images from raw data, improving diagnostic accuracy. Similarly, in wireless communications, these polynomials are used to optimize signal transmission and reduce interference, enhancing the reliability and speed of data transfer.
Educational Initiatives and the Preservation of Hermite's Legacy
Preserving and promoting the legacy of Charles Hermite is crucial for inspiring future generations of mathematicians and scientists. Educational initiatives around the world are dedicated to teaching Hermite's theories and methodologies, ensuring that his contributions continue to influence mathematical research and education.
Mathematical Competitions and Hermite's Theorems
Mathematical competitions, such as the International Mathematical Olympiad (IMO) and the Putnam Competition, often feature problems inspired by Hermite's work. These competitions challenge students to apply Hermite's theories in creative and innovative ways, fostering a deeper understanding of advanced mathematical concepts.
By engaging with Hermite's proofs and methodologies, students develop critical thinking skills and a greater appreciation for the beauty and elegance of mathematical reasoning. These competitions play a vital role in identifying and nurturing young mathematical talent, ensuring the continued advancement of the field.
Online Resources and Digital Archives
The digital age has made it easier than ever to access and study Hermite's original works and related research. Online platforms such as arXiv, JSTOR, and Project Euclid provide open access to a vast array of mathematical literature, including papers and books that build upon Hermite's contributions.
Educational institutions and mathematical societies have also created digital archives dedicated to preserving Hermite's legacy. These resources include digitized versions of his original manuscripts, lecture notes, and correspondence, offering invaluable insights into his mathematical thought process and collaborative efforts.
Conclusion: The Everlasting Impact of Charles Hermite
Charles Hermite's contributions to mathematics have left an indelible mark on the field, influencing generations of mathematicians and shaping the course of scientific progress. His groundbreaking work on transcendental numbers and Hermite polynomials has not only advanced theoretical mathematics but also found practical applications in diverse technological domains.
The connection between Hermite's methodologies and the foundational principles of ancient Greek mathematics highlights the timeless nature of mathematical inquiry. By building upon the axiomatic methods of Euclid and the exhaustive techniques of Archimedes, Hermite's achievements exemplify the continuous evolution of mathematical thought and its enduring relevance.
As we look to the future, the applications of Hermite's work are set to expand even further, particularly in emerging fields such as quantum computing and artificial intelligence. These advancements underscore the profound impact that fundamental mathematical research can have on our understanding of the universe and our ability to innovate and solve complex problems.
In conclusion, Charles Hermite's legacy serves as a testament to the power of human ingenuity and the boundless potential of mathematical discovery. His work continues to inspire and challenge mathematicians, scientists, and engineers, driving progress and shaping the future of theoretical and applied sciences. As we celebrate his contributions, we are reminded of the enduring importance of rigorous mathematical reasoning and the timeless pursuit of knowledge.
"Mathematics is the music of reason, and Charles Hermite composed some of its most beautiful symphonies."





