Explore Any Narratives
Discover and contribute to detailed historical accounts and cultural stories. Share your knowledge and engage with enthusiasts worldwide.
The intriguing phrase "H-Symbol of Emy Neter in Mathematics and Physics" opens a fascinating gateway into interdisciplinary exploration. While not a standard term in academic lexicons, it invites an investigation into symbolic language, historical figures, and cultural intersections within the sciences. This article will unravel the most plausible interpretations, anchoring them in the rich contexts of Greek educational frameworks and global scientific discourse. Our journey connects potential meanings, from iconic mathematical operators to transformative historical legacies.
Understanding this topic requires navigating both precise scientific terminology and broader cultural narratives. The Greek educational system provides a crucial backdrop, with its structured emphasis on mathematics and physics shaping public engagement with these fields. Recent trends show a growing interest in programs that blend scientific rigor with philosophical and historical inquiry, particularly within Greece itself.
The initial challenge lies in decoding the original string. It appears to be a romanized version of a potential Greek title. Several key interpretations emerge from careful analysis, each leading down a distinct yet enlightening path. These paths converge on the enduring human quest to use symbols and names to explain the fundamental laws of nature.
In formal science, the letter H often denotes pivotal concepts. In physics, it universally represents the Hamiltonian operator, the cornerstone of classical and quantum mechanics that encapsulates a system's total energy. In mathematics, H appears in various contexts, from Hecke operators in number theory to the Hilbert space in functional analysis.
However, no widely recognized "H-Symbol of Emy Neter" exists in indexed literature. This absence suggests the phrase may be a creative or localized title rather than a technical term. It could symbolize a conceptual bridge or a personalized pedagogical tool within a specific educational or cultural project.
The most compelling and educationally significant interpretation involves a probable transliteration error. The name "Emy Neter" strongly resembles "Emmy Noether," the legendary German mathematician. Emmy Noether's groundbreaking theorems fundamentally linked symmetry principles to conservation laws in physics, a concept central to modern theoretical physics.
If the intended subject is "The Significance of Emmy Noether in Mathematics and Physics," the topic is profoundly rich. Noether's work is a pillar of contemporary science, making this hypothesis highly plausible for any discussion seeking to connect deep mathematical ideas to physical law.
Noether's theorem is often described as one of the most important mathematical results in theoretical physics, guiding everything from classical mechanics to quantum field theory.
Alternatively, "Neter" could reference the ancient Egyptian term "nṯr" (neter/netjer), meaning a divine force or god. This opens an interdisciplinary, cultural lens. A phrase combining "neter" with Greek words for mathematics and physics might explore the historical personification of natural forces or the philosophical origins of scientific thought.
Such a theme aligns with modern interdisciplinary programs in Greece and globally that examine the history and philosophy of science. This interpretation, while not mainstream science, reflects a growing academic interest in the cultural roots of scientific inquiry.
To fully appreciate where such a topic might emerge, one must understand its potential incubator. The Greek education system maintains a strong, structured focus on the core sciences, creating an audience keenly interested in the intersections of mathematics, physics, and culture.
In Greek upper secondary education, the teaching hours dedicated to mathematics and physics are substantial and vary by student specialization. This structured exposure cultivates a foundational literacy in these subjects among a significant portion of the population.
This curricular emphasis ensures that topics blending mathematical rigor and physical principles resonate within the Greek educational landscape. It provides a ready audience for discussions that extend beyond pure textbook formulas into historical and philosophical dimensions.
The Greek academic scene actively fosters cross-disciplinary dialogue. Recent years have seen a proliferation of conferences, summer schools, and workshops that intentionally bridge STEM fields with the humanities, history, and philosophy.
For instance, events like the PHYSIS Summer School explicitly explore the connections between ancient conceptions of nature and modern science. Such programs demonstrate an institutional environment where a title mixing Greek language, symbolic concepts, and scientific themes would be perfectly at home.
These trends create a fertile ground for the kind of nuanced exploration suggested by our core phrase. They indicate that the discussion is not happening in a vacuum but within a vibrant, engaged intellectual community.
If "Emy Neter" is indeed a reference to Emmy Noether, then the discussion enters the realm of foundational scientific legacy. Noether's theorem represents one of the most profound connections between abstract mathematics and tangible physical law. Her work demonstrated that every differentiable symmetry of a physical system corresponds to a conservation law.
This principle is a cornerstone of modern theoretical physics. It directly links, for example, the symmetry of time translation to the conservation of energy. Her innovations in abstract algebra also reshaped mathematics, establishing her as a towering figure whose influence permeates both disciplines. Exploring her significance provides a clear, impactful narrative for the original phrase.
The power of Noether's theorem lies in its universal applicability. From classical mechanics, where it explains the conservation of momentum, to quantum field theory and the Standard Model of particle physics, her insight is indispensable. The theorem provides a critical tool for physicists to derive conserved quantities directly from the observed symmetries of a system.
This deep interconnection means that studying symmetry is not merely an aesthetic or mathematical exercise. It is a direct pipeline to understanding the fundamental constants and rules governing the universe. The theorem is a mandatory component of advanced physics curricula worldwide, underscoring its non-negotiable importance.
Albert Einstein described Emmy Noether as "the most significant creative mathematical genius thus far produced since the higher education of women began."
Noether's story is also one of perseverance against significant institutional barriers. As a woman in early 20th-century academia, she faced immense challenges in gaining recognition and a formal position. Her work was initially undervalued, yet its sheer intellectual force eventually made it impossible to ignore.
Her legacy today is twofold: she is celebrated for her transformative scientific contributions and revered as an icon for women in STEM. This dual significance makes her a highly relevant subject for contemporary educational discourse, particularly in discussions about inclusivity and recognizing hidden figures in science history.
If the "H-Symbol" is interpreted literally within physics, its most direct meaning is the Hamiltonian operator, denoted by H. In both classical and quantum mechanics, the Hamiltonian represents the total energy of a system—the sum of its kinetic and potential energies. This single symbol encodes the entire dynamics of a physical system.
Hamiltonian mechanics provides a powerful framework for analyzing complex systems, from planetary orbits to quantum states. The centrality of H in the fundamental equations of physics makes it one of the most important symbols in the scientific lexicon. Its utility extends into cutting-edge research, including chaos theory and quantum computing.
In classical mechanics, the Hamiltonian formalism allows physicists to work with generalized coordinates and momenta. This approach simplifies solving problems involving constraints and complex motions. The equations derived from H provide a clear, symmetric path to understanding a system's evolution over time.
In quantum mechanics, the Hamiltonian takes on an even more crucial role. It becomes an operator whose eigenvalues correspond to the possible energy levels a system can occupy. Solving the time-independent Schrödinger equation, Hψ = Eψ, is the primary task for understanding atomic and subatomic structures.
The Hamiltonian framework is not a historical relic but a living tool. In quantum computing, designing Hamiltonians is essential for simulating complex molecules and materials. Researchers manipulate H to model chemical reactions and discover new properties of matter in ways impossible with classical computers alone.
Similarly, in condensed matter physics, topological phases of matter are classified using Hamiltonian analysis. The symbol H, therefore, sits at the very frontier of our understanding of the universe, from the infinitesimally small to the cosmological scale. Its enduring relevance underscores why a "symbol" can hold such immense conceptual weight.
The alternative interpretation, focusing on the ancient Egyptian concept of "neter," leads to a rich exploration of science's historical and philosophical roots. This path examines how early civilizations personified natural forces and sought to explain the cosmos through symbolic and divine frameworks, a precursor to later mathematical modeling.
This interdisciplinary angle connects the history of science, philosophy, and cultural studies. It asks how humanity's quest to understand nature evolved from mythological narratives to the quantitative, symbol-driven language of modern physics and mathematics. Such exploration is increasingly present in academic programs that value a holistic view of knowledge.
Many ancient cultures, including the Egyptians, Greeks, and Mesopotamians, developed sophisticated cosmologies. They used symbolic language and personified deities (neteru) to describe the orderly principles they observed in the natural world—the movement of stars, the flooding of the Nile, or the cycle of life and death.
This symbolic representation was an early form of scientific modeling. While the methods differ radically, the underlying impulse—to find order and rule in nature—is the same driving force behind modern science. Studying these ancient systems can provide valuable historical context for the development of abstract thought.
The Greek educational system's recent interdisciplinary programs, such as those exploring "Math and Physics of the Ancient World," explicitly create space for this kind of comparative historical analysis.
Today, there is a renewed scholarly interest in how ancient knowledge systems can inform contemporary thinking. This is not about validating outdated science but about understanding the cognitive and cultural pathways that led to formal logic, geometry, and empirical investigation. The Greek word "φύσις" (physis), meaning "nature," is itself the root of "physics."
Programs and conferences in Greece and internationally are actively building these bridges. They examine, for instance, how Greek geometry and Egyptian practical mathematics converged and diverged. A phrase invoking "neter" in the context of math and physics could well be the title of a lecture or paper within such a forward-looking yet historically grounded forum.
The journey through the possible meanings of "H-Symbol of Emy Neter" reveals a common thread: the immense power of symbolic language in advancing human understanding. Whether through the precise operator H, the legacy of a genius like Noether, or the ancient symbolism of neter, humanity uses abstraction to grasp complex realities. This synthesis highlights the interdisciplinary nature of true scientific progress.
Mathematics and physics do not exist in a cultural vacuum. They are products of historical context, philosophical inquiry, and the relentless human drive to codify the universe. Recognizing this interconnectedness enriches our appreciation of both the sciences and the humanities. It demonstrates that symbols are bridges between intuition, observation, and formal proof.
The structure of the Greek educational system, with its balanced curriculum, provides a foundation for this kind of broad thinking. By allocating significant weekly hours to both mathematics and physics, it ensures students develop the necessary literacy to engage with complex ideas. Recent trends toward specialized summer schools and conferences further promote synthesis.
Programs that connect ancient philosophy with modern physics or explore the history of mathematical notation are directly cultivating this integrative mindset. They prepare students not just to calculate but to contextualize, which is a critical skill for the next generation of innovators and thinkers. This educational direction aligns with global movements toward STEM/STEAM integration.
Focusing on the most plausible interpretation, the significance of Emmy Noether cannot be overstated. Her work is a prime example of how pure mathematical insight can unlock fundamental truths about the physical world. Noether's theorem is more than a formula; it is a philosophical principle that symmetry and conservation are two faces of the same coin.
In today's research frontiers, from the search for new particles at the Large Hadron Collider to theoretical work on quantum gravity, Noether's principles remain actively used. They are foundational to the Standard Model of particle physics, where gauge symmetries dictate the forms of all fundamental interactions. This demonstrates the timeless applicability of her 20th-century breakthrough.
Modern theoretical physics heavily relies on the framework established by Noether. The development of gauge theories, which describe the electromagnetic, weak, and strong nuclear forces, is deeply rooted in symmetry principles. Each force is associated with a specific symmetry, and the corresponding conserved quantities are derived directly from Noether's theorem.
Even in speculative areas like string theory and loop quantum gravity, the quest for underlying symmetries guides research. The theorem provides a reliable compass in the highly abstract landscape of theoretical physics. It ensures that new proposals remain grounded in the established conservation laws that have been experimentally verified for over a century.
"Noether's work permanently altered the landscape of theoretical physics and mathematics, proving that profound abstraction yields concrete physical predictions."
Greece's contemporary academic scene is poised to be a fertile ground for discussions that mirror the ambiguous title we began with. The country's unique position—as the birthplace of Western science and philosophy and a modern EU member with a robust educational system—makes it an ideal host for fusion-oriented intellectual events.
The data shows a clear pattern of conferences, summer schools, and courses designed to break down disciplinary silos. This environment is precisely where a topic blending a symbolic "H," a historical figure ("Emy Neter"), and the hard sciences could naturally emerge and thrive.
Recent years have seen a measurable increase in cross-disciplinary offerings. For example, event listings show a significant number of physics and mathematics conferences scheduled in Greece for 2025-2026, many with themes connecting to history, philosophy, or education. These are not niche gatherings but established, respected academic venues.
Furthermore, analysis of university entry scores and subject preferences indicates a sustained student interest in the core sciences. This creates a pipeline of engaged minds ready to tackle complex, synthesized ideas. The infrastructure for deep, meaningful dialogue at the intersection of culture and science is actively being built and utilized.
The exploration of the phrase "H-Symbol of Emy Neter in Mathematics and Physics" has taken us from technical definitions to historical biography and cultural analysis. This journey underscores a vital point: ambiguity in language can be a powerful catalyst for broader understanding. It forces us to consider multiple perspectives and uncover connections we might otherwise miss.
The most direct path likely leads to the monumental legacy of Emmy Noether and the Hamiltonian operator. This connection provides a rich, evidence-based narrative full of educational value and scientific importance. It highlights a key figure whose work is a cornerstone of modern theoretical physics and a testament to the power of abstract thought.
Several crucial insights emerge from this investigation. First, the importance of precise terminology and historical context in scientific communication cannot be ignored. Second, the Greek educational framework is actively supporting the kind of interdisciplinary thinking that makes such explorations possible. Finally, the enduring relevance of foundational ideas, whether from the early 20th century or ancient civilizations, continues to shape contemporary inquiry.
Educators can use this multifaceted topic as a case study in how science evolves. It shows how ideas travel, transform, and sometimes get rediscovered under new names. It demonstrates that the history of science is not a linear march but a rich tapestry woven from diverse threads of human curiosity.
Ultimately, whether the original phrase was a transliteration error, a creative title, or a niche project name matters less than the discussion it generates. It points toward a future where scientific rigor and humanistic inquiry are not adversaries but partners. In a world facing complex global challenges, this integrated approach to knowledge is not just academically interesting—it is essential.
The next generation of problem-solvers will need to think symbolically, historically, and scientifically all at once. They must appreciate the Hamiltonian's elegance, understand Noether's struggle for recognition, and grasp how ancient civilizations sought patterns in nature. By embracing the full spectrum of meaning behind a simple string of words, we take a small but significant step toward that more holistic, and more human, understanding of our universe.
Your personal space to curate, organize, and share knowledge with the world.
Discover and contribute to detailed historical accounts and cultural stories. Share your knowledge and engage with enthusiasts worldwide.
Connect with others who share your interests. Create and participate in themed boards about any topic you have in mind.
Contribute your knowledge and insights. Create engaging content and participate in meaningful discussions across multiple languages.
Already have an account? Sign in here

Max Born was a renowned theoretical physicist and Nobel laureate known for his statistical interpretation of quantum mec...
View Board
Discover the remarkable life and enduring legacy of Arturo Miolati, a trailblazer whose groundbreaking work in quantum m...
View Board
"Explore Jacques Hadamard's legacy: Prime Number Theorem proof, functional analysis, and impact on modern tech. Discover...
View Board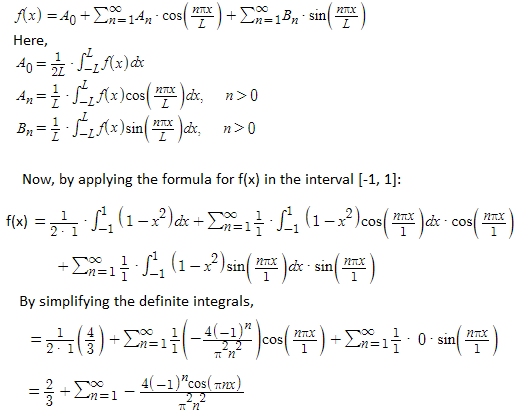
Explore the life and groundbreaking innovations of Jean-Baptiste Joseph Fourier, the French mathematician and physicist ...
View Board
Explore the life of Paul Painlevé, a groundbreaking mathematician and innovative political leader, whose dual legacy in ...
View Board
George Gamow: The Unbelievable Journey of a Theoretical Physicist and Cosmologist The Enigmatic Man Behind the Cosmic B...
View Board
Jean Baptiste Joseph Delambre: A Life of Astronomical Pursuits The Early Life and Education Jean Baptiste Joseph Delam...
View BoardÉmile Borel: A Pioneering Mathematician and Physicist The Early Life and Education of Émile Borel Émile Borel, born on...
View Board
Explore Roger Penrose's groundbreaking contributions to physics, black holes, quantum consciousness, and aperiodic tilin...
View Board
Explore the life and enduring legacy of Julio Palacios, a pioneering physicist from the 20th century whose groundbreakin...
View Board
Explore the remarkable legacy of Henri Cartan, the pioneering mathematician whose groundbreaking contributions to algebr...
View Board
Isaac Newton was a pioneering scientist whose laws of motion and universal gravitation revolutionized our understanding ...
View Board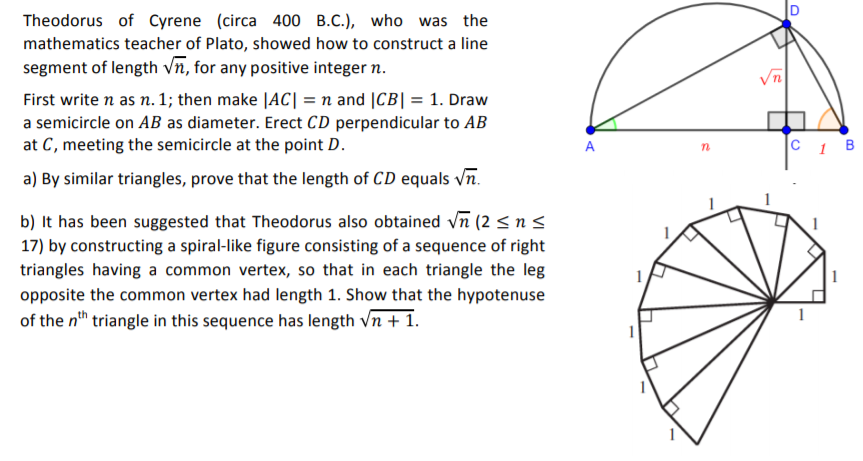
Theodorus of Cyrene, the ancient Greek mathematician and Plato's teacher, revolutionized geometry with his work on irrat...
View Board
Discover the life of Aldo Pontremoli, a pioneering Italian physicist who founded Italy's first physics institute and joi...
View Board
Discover the enduring legacy of Jean-Baptiste Biot, a remarkable polymath at the crossroads of Enlightenment and 19th-ce...
View Board
Discover the groundbreaking achievements of Alain Aspect, the quantum physicist who transformed our understanding of rea...
View Board
Discover the enduring legacy of Léon Brillouin, a 20th-century visionary physicist who bridged theoretical and applied s...
View Board
Explore the extraordinary journey of Franklin Chang-Díaz, from Costa Rica to the cosmos, in this comprehensive article. ...
View Board
"Explore Henri Poincaré's groundbreaking work in math, physics, and philosophy, shaping modern science through chaos the...
View Board
Discover the transformative journey of Sir Isaac Newton, the prodigious mind who redefined science with groundbreaking t...
View Board
Comments