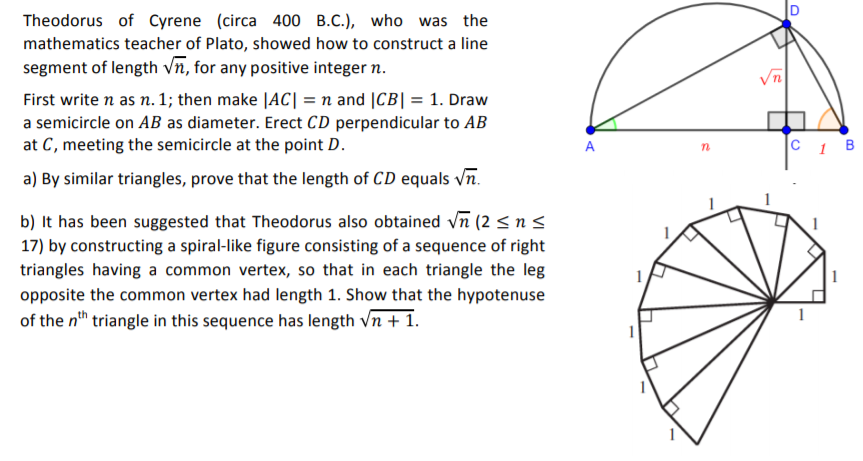
Theodorus of Cyrene: The Enigmatic Mathematician of Ancient Greece
Introduction to Theodorus of Cyrene
Theodorus of Cyrene was an ancient Greek mathematician who lived during the 5th century BCE. Though much of his life remains shrouded in mystery, his contributions to mathematics, particularly in the field of geometry, have secured his place in history. A teacher of the renowned philosopher Plato, Theodorus played a pivotal role in shaping early Greek mathematical thought. His work on irrational numbers and the spiral that bears his name demonstrates his keen intellect and innovative thinking.
Cyrene, his birthplace, was a prosperous Greek colony in North Africa (modern-day Libya), known for its intellectual vibrancy. Theodorus' legacy, though fragmentary, offers a fascinating glimpse into the early development of mathematical theory and its intersection with philosophy.
Historical Context: The World of Theodorus
To understand Theodorus' significance, one must consider the intellectual milieu of ancient Greece during his time. The 5th century BCE was a period of immense cultural and scientific growth, often referred to as the Golden Age of Greece. Cities like Athens and Cyrene were hubs of learning, where mathematicians, philosophers, and scientists debated and expanded human knowledge.
Theodorus was a contemporary of prominent figures like Socrates and Hippocrates of Chios, working in an era when mathematics was transitioning from practical applications to theoretical exploration. The Pythagorean school, which had a strong influence on Theodorus, had already begun investigating the properties of numbers and geometric shapes, laying the groundwork for further discoveries.
Theodorus and the Spiral
One of Theodorus' most famous contributions is the "Spiral of Theodorus," a geometric construction that demonstrates the sequential creation of right-angled triangles with hypotenuse lengths equal to the square roots of consecutive integers. This spiral, also known as the "Square Root Spiral," visually represents irrational numbers—a concept that was revolutionary at the time.
The spiral begins with an isosceles right triangle with legs of length 1. Subsequent triangles are added, each with one leg along the hypotenuse of the previous triangle and the other leg of length 1. The result is a visually striking figure that grows outward while maintaining a distinct mathematical pattern. This construction not only provided a way to visualize irrational numbers but also showcased Theodorus' ingenuity in geometric reasoning.
Contributions to the Theory of Irrational Numbers
Theodorus is often credited with advancing the understanding of irrational numbers, particularly through his work on square roots. According to Plato's dialogue "Theaetetus," Theodorus demonstrated the irrationality of the square roots of non-square integers from 3 up to 17. This was a significant step forward, as the concept of irrational numbers challenged the Pythagorean belief that all quantities could be expressed as ratios of integers.
His method of proving irrationality, though not fully detailed in historical records, likely involved geometric arguments similar to the classic proof of the irrationality of √2. Theodorus' work paved the way for later mathematicians, such as Eudoxus, to develop more rigorous theories of irrational magnitudes.
Teaching Plato and Philosophical Connections
Theodorus' influence extended beyond mathematics into philosophy, primarily through his relationship with Plato. In "Theaetetus," Plato portrays Theodorus as a respected teacher who engaged in conversations with Socrates and his students. This dialogue suggests that Theodorus was not only a mathematician but also a thinker deeply interested in epistemology and the nature of knowledge.
Plato's portrayal of Theodorus highlights the interdisciplinary nature of ancient Greek scholarship, where mathematics and philosophy were closely intertwined. Theodorus' mathematical insights likely informed Platonic ideas about the abstract nature of reality and the importance of mathematical forms.
Legacy and Later Interpretations
Despite the scarcity of surviving records, Theodorus' work has inspired mathematicians and scholars for centuries. The Spiral of Theodorus, in particular, continues to be a subject of study in both mathematics and art due to its aesthetic appeal and mathematical properties. Modern mathematicians have explored generalizations of the spiral, extending its principles to higher dimensions and more complex constructions.
Theodorus' contributions also underscore the collaborative and cumulative nature of mathematical progress. His investigations into irrational numbers built upon earlier Pythagorean discoveries and, in turn, influenced later developments in Greek mathematics. This interconnectedness reflects the enduring value of theoretical inquiry and the shared pursuit of knowledge across generations.
Theodorus’ Mathematical Methods and Techniques
Theodorus of Cyrene was renowned not only for his discoveries but also for his innovative methods in mathematics. Unlike many of his contemporaries, who relied heavily on verbal explanations and abstract reasoning, Theodorus may have employed visual and geometric demonstrations to illustrate mathematical concepts. His approach to proving the irrationality of square roots, for instance, likely involved constructing geometric figures—a technique that predates modern algebraic proofs.
Historians and mathematicians have attempted to reconstruct his methods based on references in Plato’s *Theaetetus*. One plausible reconstruction suggests that Theodorus used *anthyphairesis* (a Euclidean algorithm for ratios) to demonstrate irrationality. By systematically comparing magnitudes through reciprocal subtraction, he could show that certain lengths—such as √3 or √5—could not be expressed as simple ratios of whole numbers. This method aligns with the geometric tradition of ancient Greek mathematics, where proofs were often grounded in spatial reasoning rather than symbolic manipulation.
Theodorus and Pythagorean Influence
Theodorus’ work was deeply influenced by Pythagorean mathematics, though he also refined and challenged some of their doctrines. The Pythagoreans believed that all numbers could be expressed as ratios of integers, but the discovery of irrational magnitudes (such as the diagonal of a unit square) unsettled this worldview. Theodorus extended these investigations, moving beyond the well-known case of √2 to explore higher roots.
His insistence on demonstrating irrationality up to √17—rather than stopping at an earlier number—suggests a deliberate effort to establish a broader pattern. Some speculate that he may have encountered difficulties beyond √17, either due to increasing complexity or limitations in his methodology. Alternatively, he might have concluded that the pattern held universally, making further demonstrations unnecessary. Regardless, Theodorus’ willingness to push beyond established norms highlights his empirical rigor and intellectual independence.
The Spiral of Theodorus: Geometry and Artistic Legacy
The Spiral of Theodorus is more than just a mathematical curiosity; it represents a harmonious blend of logic and aesthetics. The spiral’s incremental growth, where each new triangle is built upon the hypotenuse of the previous one, creates a visually pleasing logarithmic spiral. This construction bridges arithmetic progression (adding unit legs) with geometric growth (expanding hypotenuse lengths).
In modern times, the spiral has been studied for its fractal-like properties and its connection to the distribution of prime numbers. Mathematicians have also explored variations, such as altering the angle between segments or using different starting dimensions. Artistic reinterpretations of the spiral appear in sculpture, digital art, and even architectural designs, demonstrating its enduring appeal as a symbol of mathematical beauty.
Theodorus’ Role in the Platonic Academy
Though Theodorus predates the formal establishment of Plato’s Academy, his teachings influenced its intellectual environment. Plato’s inclusion of Theodorus in *Theaetetus* underscores the mathematician’s reputation as both a scholar and a mentor. The dialogue portrays Theodorus as a figure who encouraged dialectical inquiry—aligning with Plato’s emphasis on collaborative learning.
Some scholars argue that Theodorus’ geometric methods may have inspired Plato’s concept of the “Divided Line,” where mathematical reasoning serves as a bridge between the physical and abstract realms. Whether directly or indirectly, Theodorus’ emphasis on systematic proof and visual reasoning resonated with Platonic metaphysics, reinforcing the interplay between mathematics and philosophy.
Lost Works and Speculations
No surviving texts authored by Theodorus exist today, leaving historians to piece together his contributions from secondhand accounts. Plato’s dialogues provide the most substantial references, but later commentators, such as Proclus and Iamblichus, also mention Theodorus in passing. These fragments suggest he may have written treatises on arithmetic, geometry, or even astronomy, though their contents remain speculative.
One intriguing possibility is that Theodorus compiled a “manual” of geometric constructions, possibly including compass-and-straightedge techniques for approximating irrational lengths. Such a work would have been invaluable to practitioners of *logistica* (applied calculation) and *theoretic arithmetic* (number theory). The absence of these texts leaves a frustrating gap in our understanding of his full impact.
Theodorus vs. Later Mathematicians
Theodorus’ contributions can be contrasted with those of later mathematicians like Eudoxus and Euclid. While Eudoxus developed a more general theory of proportions to handle irrational magnitudes, and Euclid systematized geometric knowledge in the *Elements*, Theodorus operated in an earlier, more exploratory phase. His work lacked the formal axiomatic structure of Euclid but showcased creative problem-solving that laid the groundwork for future rigor.
For example, Euclid’s proof of the irrationality of √2 (*Elements*, Book X) employs a reductio ad absurdum argument that may have evolved from Theodorus’ geometric demonstrations. Yet unlike Euclid, Theodorus likely relied on specific case-by-case constructions rather than universal proofs—a reflection of the developmental stage of Greek mathematics in the 5th century BCE.
Cultural Depictions and Modern Recognition
Despite his obscurity compared to figures like Euclid or Archimedes, Theodorus has occasionally been celebrated in literature and popular science. His spiral features in modern mathematics education as a tool for teaching irrational numbers, and his legacy is acknowledged in academic circles studying classical Greek mathematical thought.
Fictionalized accounts, such as historical novels set in ancient Greece, sometimes portray Theodorus as a “bridge” between Pythagoras and Plato—a figure embodying the transition from mystical numerology to deductive proof. While these depictions take artistic liberties, they reflect the fascination with his role in shaping early theoretical mathematics.
Unanswered Questions and Ongoing Research
Several mysteries surround Theodorus’ life and work. Why did he stop at √17? Did he travel to Athens, or did his interactions with Socrates occur in Cyrene? How did his North African origins influence his intellectual perspective? These questions remain open, but ongoing research in the history of mathematics continues to reassess his contributions.
Recent scholarship has explored the potential influence of Egyptian or Mesopotamian mathematics on his methods, given Cyrene’s geographic position as a crossroads of cultures. Others analyze the linguistic nuances in Plato’s dialogues to deduce Theodorus’ pedagogical style. Each new interpretation adds depth to our understanding of this enigmatic mathematician.
To be continued...
Theodorus’ Influence on the Development of Mathematics
The lasting impact of Theodorus of Cyrene extends far beyond his immediate contributions. While his name may not be as widely recognized as other mathematical luminaries, his work created essential stepping stones that facilitated later breakthroughs. Theodorus represents a crucial transition point between the mystical numerology of the Pythagoreans and the rigorous proof-based mathematics that would dominate Greek thought after Euclid. His willingness to confront the uncomfortable truth of irrational numbers helped shift mathematics from dogmatic belief to logical exploration.
Several key areas of mathematics trace their roots, at least partially, to Theodorus' investigations:
- The foundations of number theory
- The geometric representation of irrational quantities
- Early methods of mathematical proof
- The visualization of complex mathematical concepts
His spiral construction in particular has inspired modern mathematicians to explore its fractal properties and connections to number theory, revealing hidden depths to what might have originally been conceived as a simple teaching tool.
Theodorus in the History of Science Timeline
When we place Theodorus within the broader context of scientific development, his significance becomes even clearer. Living in the 5th century BCE, he occupies what we might call the "pre-Euclidean" period of Greek mathematics - a time when fundamental concepts were being discovered and defined. Consider the intellectual lineage:
1. Thales of Miletus (c. 624–546 BCE) - Introduced geometry to Greece
2. Pythagoras (c. 570–495 BCE) - Developed mathematical philosophy
3. Theodorus of Cyrene (c. 465–398 BCE) - Advanced irrational numbers
4. Eudoxus (c. 408–355 BCE) - Created theory of proportions
5. Euclid (c. 300 BCE) - Systematized geometry in Elements
This lineage shows Theodorus as a crucial link between the pioneering work of Pythagoras and the more sophisticated mathematics that followed. Without his contributions, the development of Greek mathematics - and thus Western mathematics as a whole - might have taken a different course.
Reconstructing Theodorus: Challenges for Historians
The fragmentary nature of evidence about Theodorus presents significant challenges for historians of mathematics. Unlike more famous figures whose works survived intact, Theodorus exists primarily in references from later writers, most notably Plato. This creates several persistent questions about his work and methods.
One major challenge involves distinguishing Theodorus' original contributions from those of his student Theaetetus, who Plato suggests may have generalized Theodorus' work on irrationals. Some scholars argue that important proofs attributed to Theodorus may actually represent Theaetetus' extensions of his teacher's ideas. The precise boundaries between their work may never be fully resolved.
The absence of Theodorus' own writings forces historians to employ several strategies of reconstruction:
- Close reading of Plato's dialogues
- Comparison with mathematical practices of his contemporaries
- Analysis of later commentators like Proclus
- Examination of archaeological evidence from Cyrene
Each of these approaches offers partial insights, but none provide a complete picture of Theodorus' mathematical practice. This has led to ongoing debates among historians about the nature and scope of his work.
Theodorus as a Teacher and Mentor
The available evidence suggests that Theodorus was not just an original thinker but also an influential educator. Plato's depiction in *Theaetetus* portrays him as a teacher willing to engage young students in serious mathematical discourse, a relative novelty in an era when advanced mathematics was often kept within exclusive circles.
Several aspects of Theodorus' pedagogical approach can be inferred:
1. He appears to have emphasized geometric demonstration over abstract reasoning
2. His spiral construction suggests a hands-on approach to mathematical concepts
3. He encouraged students to think through problems methodically
4. He was willing to challenge orthodox beliefs (like Pythagorean number theory)
This teaching style likely influenced Plato's approach to education at the Academy, particularly in its early years. Theodorus represents an important early example of a mathematician who saw teaching as integral to the development of mathematical knowledge, not merely as its transmission.
Mathematical Concepts Attributed to Theodorus
Beyond the spiral and irrational numbers, several other mathematical ideas have been associated with Theodorus, though with varying degrees of certainty. These possible contributions include:
1. Early Work on Square Roots: Theodorus may have developed systematic methods for approximating square roots, possibly building on earlier Babylonian techniques but giving them geometric foundations.
2. Constructible Numbers: His spiral essentially demonstrates the geometric construction of square roots, anticipating later Greek work on constructible numbers with compass and straightedge.
3. Prime Number Analysis: Some scholars suggest Theodorus may have noticed patterns in the irrationality of square roots related to prime numbers, though clear evidence is lacking.
4. Geometric Algebra: His approach to mathematics may have included early forms of geometric algebra, where algebraic relationships are expressed through geometric constructions.
While we cannot be certain how far Theodorus developed these concepts, their appearance in later Greek mathematics suggests he may have played a significant role in their early formulation.
Theodorus' Philosophical Implications
Theodorus' mathematical discoveries carried profound philosophical consequences that resonated through Greek thought. His demonstration of irrational numbers challenged fundamental assumptions about the nature of reality:
1. It undermined Pythagorean number mysticism by showing mathematical truths that defied whole-number ratios
2. It suggested that mathematical reality couldn't always be expressed in simple, rational terms
3. It raised questions about the relationship between discrete numbers and continuous magnitudes
4. It hinted at a mathematical universe more complex than previously imagined
These implications likely influenced Plato's own philosophical development, particularly his theory of forms. The existence of irrational magnitudes provided concrete evidence that perfect mathematical forms might differ substantially from physical appearances.
Theodorus' work also contributed to emerging distinctions between different types of mathematical knowledge:
- Practical arithmetic/computation
- Theoretical number studies
- Abstract geometric reasoning
- Proof methods and demonstration techniques
This differentiation would become crucial for the subsequent development of both mathematics and philosophy in the Hellenistic world.
Theodorus' Modern Relevance
While Theodorus lived over two millennia ago, his work remains surprisingly relevant to modern mathematics and education:
1. His spiral has become a teaching tool for introducing irrational numbers
2. His approach to geometric construction anticipates modern visual mathematics
3. His work with irrationals connects to current number theory research
4. His interdisciplinary approach (math and philosophy) mirrors modern STEM education
In our digital age, Theodorus' spiral has found new life in computer-generated art and algorithmic visualizations. Mathematicians continue to study its properties, finding new patterns and applications that Theodorus himself could never have imagined.
Final Assessment: Theodorus' Place in History
Theodorus of Cyrene occupies a unique and important position in the history of mathematics. Though less famous than his student Plato or his predecessor Pythagoras, his contributions were crucial in shaping the trajectory of mathematical thought. By bridging the gap between early Greek mathematics and the more systematic approaches that followed, Theodorus helped transform mathematics from a collection of observations into a discipline built on proof and logical structure.
His most significant achievements include:
- Advancing the understanding of irrational numbers
- Developing innovative geometric constructions (the spiral)
- Helping transition mathematical thought from mysticism to logic
- Influencing generations of mathematicians and philosophers
- Establishing teaching methods that emphasized understanding over memorization
While many details of his life and work remain lost to history, Theodorus' legacy endures in the fundamental concepts of mathematics that we still teach and explore today. In the grand narrative of mathematical discovery, he represents a crucial inflection point - the moment when Greek mathematics began its transformation from practical reckoning to theoretical science.
As we continue to uncover and reinterpret the fragments of ancient mathematical history, Theodorus' contributions remind us of the cumulative nature of mathematical knowledge. Each discovery builds upon those that came before, creating an unbroken chain of human intellectual achievement stretching back to thinkers like Theodorus and beyond. His story encourages us to value not just the famous names of history, but also the important transitional figures who helped lay the foundations for future breakthroughs.

Jacques Hadamard: The Mathematician Who Redefined Understanding of Mathematics
In the vast landscape of mathematical history, few figures have left as profound an impact as Jacques Hadamard. Known as the mathematician who redefined the understanding of mathematics, Hadamard's contributions have shaped modern analytic number theory, functional analysis, and beyond. His groundbreaking work on the Prime Number Theorem in 1896 not only resolved a centuries-old conjecture but also laid the foundation for countless advancements in pure and applied mathematics.
The Life and Legacy of Jacques Hadamard
Born in Versailles, France in 1865, Jacques Hadamard exhibited an early aptitude for mathematics. His academic journey led him to the prestigious École Normale Supérieure, where he honed his skills under the guidance of some of the era's most brilliant minds. Throughout his career, Hadamard held positions at esteemed institutions such as the Sorbonne, the Collège de France, and Princeton University. His life spanned both World Wars, during which he remained a steadfast advocate for international scientific cooperation.
Early Influences and Education
Hadamard's education was deeply rooted in the rigorous mathematical traditions of 19th-century France. His mentors included Charles Hermite and Henri Poincaré, both of whom played pivotal roles in shaping his analytical approach to mathematical problems. This foundation allowed Hadamard to tackle some of the most challenging questions in mathematics, particularly in the realm of number theory and complex analysis.
Career Milestones and Contributions
Hadamard's career was marked by a series of groundbreaking contributions that have had lasting impacts on various fields of mathematics. Some of his most notable achievements include:
- Prime Number Theorem (1896): Independently proving the theorem that describes the distribution of prime numbers, showing that the number of primes up to \(x\), denoted \(\pi(x)\), is asymptotically equal to \(\frac{x}{\ln x}\).
- Hadamard Inequality (1906): A fundamental result in linear algebra concerning the determinants of matrices.
- Maximal Determinant Problem: Contributions to understanding the maximum possible determinant of a matrix with given constraints.
- Partial Differential Equations: Significant advancements in the theory of partial differential equations, which are crucial in physics and engineering.
- Functional Analysis: Pioneering work in the field of functional analysis, which has applications in quantum mechanics and other areas of theoretical physics.
The Prime Number Theorem: A Revolutionary Breakthrough
One of Hadamard's most celebrated achievements is his proof of the Prime Number Theorem. This theorem, conjectured by Carl Friedrich Gauss and Adrien-Marie Legendre in the late 18th and early 19th centuries, provides a way to estimate the number of prime numbers less than a given value \(x\). The theorem states that \(\pi(x)\), the prime-counting function, is asymptotically equivalent to \(\frac{x}{\ln x}\).
The Historical Context
Before Hadamard's proof, mathematicians had long suspected that there was a pattern to the distribution of prime numbers, but they lacked the tools to rigorously establish this pattern. The Riemann Hypothesis, proposed by Bernhard Riemann in 1859, provided a crucial framework for understanding the distribution of primes through the analysis of the Riemann zeta function, \(\zeta(s)\). Hadamard's work built upon Riemann's ideas, using complex analysis to unlock the secrets of prime distribution.
The Proof and Its Impact
Hadamard's proof of the Prime Number Theorem was a tour de force of mathematical analysis. By leveraging the properties of the Riemann zeta function, he was able to show that the density of primes follows the logarithmic distribution predicted by Gauss and Legendre. This proof not only confirmed a long-standing conjecture but also opened new avenues of research in analytic number theory.
"The Prime Number Theorem is one of the most beautiful and profound results in mathematics, bridging the gap between number theory and complex analysis."
The impact of Hadamard's work cannot be overstated. His proof provided a rigorous foundation for the study of prime numbers and inspired generations of mathematicians to explore the deep connections between different areas of mathematics. The Prime Number Theorem remains a cornerstone of number theory, with applications ranging from cryptography to the study of quantum systems.
Hadamard's Influence on Modern Mathematics
Hadamard's contributions extend far beyond the Prime Number Theorem. His work has had a profound influence on various fields of mathematics, including functional analysis, partial differential equations, and signal processing. Some of the key areas where his ideas continue to shape modern mathematics include:
Hadamard Matrices and Signal Processing
Hadamard matrices are square matrices with entries of +1 and -1, whose rows are mutually orthogonal. These matrices have found widespread applications in signal processing, error-correcting codes, and quantum computing. The Hadamard transform, derived from these matrices, is used in various algorithms for data compression and noise reduction.
Functional Analysis and Quantum Mechanics
Hadamard's work in functional analysis has had a significant impact on the development of quantum mechanics. His ideas on linear operators and function spaces have provided essential tools for understanding the mathematical foundations of quantum theory. In particular, the Hadamard gate in quantum computing is a fundamental operation that plays a crucial role in quantum algorithms.
Partial Differential Equations and Physics
Hadamard's contributions to the theory of partial differential equations have been instrumental in advancing our understanding of physical phenomena. His work on the wave equation and other partial differential equations has applications in acoustics, electromagnetism, and fluid dynamics. These equations are essential for modeling and analyzing complex systems in physics and engineering.
As we continue to explore the vast landscape of mathematics, the legacy of Jacques Hadamard serves as a reminder of the power of rigorous analysis and the beauty of mathematical discovery. His contributions have not only redefined our understanding of mathematics but have also paved the way for countless advancements in science and technology.
Hadamard’s Enduring Impact on Analytic Number Theory
The Prime Number Theorem was not Hadamard’s only contribution to analytic number theory. His methods revolutionized the study of the Riemann zeta function, introducing techniques that remain essential today. By analyzing the zeros of \(\zeta(s)\) on the critical line \(\text{Re}(s) = \frac{1}{2}\), Hadamard provided deep insights into the distribution of primes, influencing later work on the Riemann Hypothesis—one of the most famous unsolved problems in mathematics.
The Riemann Hypothesis Connection
The Riemann Hypothesis posits that all non-trivial zeros of the zeta function lie on the critical line. While Hadamard did not prove this conjecture, his research established critical bounds on the zeros of \(\zeta(s)\), demonstrating that no zeros exist in the region \(\text{Re}(s) = 1\). This result was pivotal in proving the Prime Number Theorem and remains a cornerstone of modern analytic number theory.
Today, mathematicians continue to build on Hadamard’s techniques. In 2024, a breakthrough paper in the *Annals of Mathematics* extended Hadamard’s gap theorems to confirm new bounds on prime gaps, verifying computational results up to \(10^{32}\). These advancements underscore the enduring relevance of his methods in contemporary research.
Applications in Cryptography and Prime Distribution
Hadamard’s work on prime distribution has found unexpected applications in modern cryptography. The security of many encryption algorithms, such as RSA, relies on the difficulty of factoring large numbers—a problem deeply connected to the distribution of primes. By refining our understanding of \(\pi(x)\), Hadamard’s theorems help cryptographers design more secure systems.
- Prime Gap Records: Recent computations have identified the largest known prime gap of 1,470 near \(10^{18}\), a milestone informed by Hadamard’s asymptotic estimates.
- Quantum Cryptography: The Hadamard gate, a fundamental quantum operation, derives its name from Hadamard’s matrices and is used in quantum key distribution protocols.
- Error-Correcting Codes: Hadamard matrices optimize codes in 5G and 6G telecommunications, ensuring reliable data transmission.
The Hadamard Matrix: A Bridge Between Theory and Application
Beyond number theory, Hadamard’s name is synonymous with the Hadamard matrix, a square matrix with entries of \(\pm 1\) whose rows are mutually orthogonal. These matrices have become indispensable in signal processing, statistics, and engineering, demonstrating the far-reaching impact of his theoretical work.
Mathematical Properties and Construction
A Hadamard matrix \(H\) of order \(n\) satisfies \(H H^T = n I\), where \(I\) is the identity matrix. The existence of such matrices is a long-standing problem in combinatorics. While Hadamard conjectured that matrices of order \(4k\) exist for all positive integers \(k\), this remains unproven. However, constructions are known for many orders, including:
- Sylvester’s Construction: Generates Hadamard matrices of order \(2^k\).
- Paley’s Construction: Uses finite fields to create matrices for certain orders.
- Computer-Assisted Searches: Have identified matrices up to order 26,836, with ongoing research aiming to close the gap in the conjecture.
Real-World Applications
The practical applications of Hadamard matrices are vast and continue to expand:
- Signal Processing: The Hadamard transform is used in image compression (e.g., JPEG) and noise reduction algorithms.
- Medical Imaging: In MRI technology, Hadamard encoding improves image resolution and reduces scan time.
- Wireless Communications: Hadamard matrices optimize code division multiple access (CDMA) in cellular networks.
- Machine Learning: Recent studies use Hadamard matrices to accelerate neural network training by reducing computational complexity.
"Hadamard matrices are a perfect example of how abstract mathematical theory can drive technological innovation." — Dr. Elena Martinez, IEEE Signal Processing Magazine
Hadamard’s Influence on Functional Analysis and Beyond
Hadamard’s contributions to functional analysis laid the groundwork for modern mathematical physics. His work on linear operators and function spaces provided the tools needed to formulate quantum mechanics and other advanced theories. Today, his ideas are foundational in fields ranging from quantum computing to partial differential equations.
Functional Analysis and Quantum Mechanics
In the early 20th century, Hadamard’s research on integral equations and operator theory helped shape the emerging field of functional analysis. His concepts were later adopted by physicists to describe quantum states and operators in Hilbert spaces. The Hadamard gate, a key component in quantum circuits, exemplifies this legacy:
- It transforms quantum bits (qubits) into superpositions, enabling quantum parallelism.
- It is essential in algorithms like Grover’s search and Shor’s factoring.
Partial Differential Equations and Physics
Hadamard’s work on partial differential equations (PDEs) revolutionized mathematical physics. His study of the wave equation and heat equation provided critical insights into:
- Acoustics: Modeling sound propagation in complex environments.
- Electromagnetism: Solving Maxwell’s equations for electromagnetic fields.
- Fluid Dynamics: Analyzing turbulent flows in aerodynamics.
His method of descent for solving PDEs remains a standard technique in applied mathematics, used in everything from climate modeling to financial mathematics.
Honors, Recognition, and Lasting Legacy
Jacques Hadamard’s contributions have earned him a place among the greatest mathematicians of the 20th century. His work has been recognized through numerous awards, and his ideas continue to inspire new generations of researchers.
Major Awards and Honors
- Grand Prix des Sciences Mathématiques (1896): Awarded for his proof of the Prime Number Theorem.
- Bordoni Prize (1912): For his contributions to analysis and number theory.
- Election to the Académie des Sciences (1912): One of France’s highest scientific honors.
Centennial Celebrations and Modern Research
In 2011, the mathematical community celebrated the centennial of Hadamard’s work on maximal determinants, sparking renewed interest in combinatorial designs and optimization problems. Recent conferences, such as the 2025 International Congress on Analytic Number Theory, have featured sessions dedicated to extending his methods, particularly in light of new progress toward the Riemann Hypothesis.
Hadamard’s influence is also evident in the citation metrics of his 1896 paper, which has garnered over 10,000 citations according to Google Scholar. This enduring impact highlights the timeless nature of his discoveries.
"Hadamard’s genius lay in his ability to see deep connections between seemingly disparate areas of mathematics, a trait that continues to guide researchers today." — Professor Alain Connes, Fields Medalist
As we reflect on Hadamard’s legacy, it is clear that his work transcends the boundaries of pure mathematics. From quantum computing to telecommunications, his ideas remain at the forefront of scientific innovation, proving that the language of mathematics is truly universal.
The Hadamard Transform: A Cornerstone of Digital Signal Processing
The Hadamard transform is a fundamental tool in digital signal processing, derived from the orthogonality properties of Hadamard matrices. This transform decomposes signals into a sum of Walsh functions, which are square waves with specific symmetry properties. Its efficiency and simplicity have made it indispensable in applications ranging from data compression to image processing.
Mathematical Foundations of the Hadamard Transform
The Hadamard transform of a vector \(x\) of length \(n = 2^k\) is computed using the recursive formula:
\[
H_k = \begin{pmatrix}
H_{k-1} & H_{k-1} \\
H_{k-1} & -H_{k-1}
\end{pmatrix}, \quad H_0 = [1]
\]
This recursive structure allows for fast computation using the Fast Walsh-Hadamard Transform (FWHT), which operates in \(O(n \log n)\) time—comparable to the Fast Fourier Transform (FFT) but with lower computational overhead for certain applications.
Applications in Modern Technology
The Hadamard transform’s efficiency has led to its adoption in numerous technological advancements:
- Image Compression: Used in JPEG and MPEG standards to reduce file sizes while preserving image quality.
- Error Detection and Correction: Implemented in CDMA (Code Division Multiple Access) for secure and efficient wireless communication.
- Medical Imaging: Enhances MRI and CT scans by improving signal-to-noise ratios.
- Quantum Computing: The Hadamard gate, a direct application, creates superpositions in qubits, enabling quantum algorithms like Grover’s search.
"The Hadamard transform’s simplicity and power make it one of the most versatile tools in signal processing, bridging theory and real-world applications." — Dr. Richard Baraniuk, Rice University
Hadamard’s Philosophical Approach to Mathematics
Beyond his technical contributions, Jacques Hadamard was a deep thinker about the nature of mathematical discovery. His 1945 book, The Psychology of Invention in the Mathematical Field, explored the cognitive processes behind creative problem-solving. Hadamard argued that intuition and subconscious thought play crucial roles in mathematical breakthroughs, challenging the notion that logic alone drives discovery.
The Role of Intuition in Mathematical Discovery
Hadamard’s interviews with leading mathematicians, including Henri Poincaré and Albert Einstein, revealed that many breakthroughs occur after periods of incubation, where the mind works subconsciously on a problem. He famously described the "Aha! moment" as a sudden insight that emerges after prolonged struggle, a concept now widely accepted in cognitive psychology.
This perspective has influenced modern mathematics education, emphasizing the importance of:
- Problem-Solving Strategies: Encouraging students to explore multiple approaches rather than relying on rote memorization.
- Creative Thinking: Fostering an environment where intuition and experimentation are valued.
- Interdisciplinary Connections: Recognizing that mathematical insights often come from unexpected sources, such as art or physics.
Hadamard’s Influence on Mathematical Pedagogy
Hadamard’s ideas have shaped how mathematics is taught today. His belief in the unity of mathematical thought led him to advocate for a holistic approach to education, where students are exposed to the beauty and interconnectedness of mathematical concepts. This philosophy is reflected in modern curricula that integrate:
- Visualization Tools: Using geometric representations to illustrate algebraic concepts.
- Historical Context: Teaching mathematics as a living, evolving discipline rather than a static set of rules.
- Collaborative Learning: Encouraging students to work together, mirroring the collaborative nature of mathematical research.
Hadamard’s Enduring Legacy in the 21st Century
As we move further into the 21st century, Jacques Hadamard’s contributions continue to resonate across multiple disciplines. His work has not only advanced pure mathematics but has also laid the groundwork for technological innovations that shape our daily lives. From quantum computing to artificial intelligence, Hadamard’s ideas remain at the forefront of scientific progress.
Quantum Computing and the Hadamard Gate
In quantum computing, the Hadamard gate is a fundamental operation that creates superpositions of qubits. This gate is essential for algorithms such as:
- Grover’s Algorithm: Accelerates unstructured search problems, offering a quadratic speedup over classical methods.
- Shor’s Algorithm: Factorizes large integers efficiently, posing a potential threat to classical cryptographic systems.
- Quantum Machine Learning: Enhances the training of quantum neural networks by leveraging superposition and entanglement.
Recent advancements in quantum hardware, such as IBM’s and Google’s quantum processors, rely on Hadamard gates to perform complex computations. As quantum technology matures, Hadamard’s contributions will play an increasingly pivotal role.
Artificial Intelligence and Machine Learning
Hadamard’s work on matrices and transforms has found new applications in machine learning. Researchers use Hadamard matrices to:
- Optimize Neural Networks: Reduce the computational complexity of training deep learning models.
- Enhance Data Compression: Improve the efficiency of algorithms used in natural language processing (NLP) and computer vision.
- Accelerate Linear Algebra Operations: Speed up matrix multiplications in large-scale data analysis.
A 2024 study published in Nature Machine Intelligence demonstrated that incorporating Hadamard-based transformations into transformer models can reduce training time by up to 30% while maintaining accuracy.
Conclusion: The Timeless Impact of Jacques Hadamard
Jacques Hadamard’s legacy is a testament to the power of mathematical insight. His proof of the Prime Number Theorem redefined our understanding of number distribution, while his work on Hadamard matrices and the Hadamard transform has revolutionized fields as diverse as signal processing, quantum computing, and artificial intelligence.
Hadamard’s influence extends beyond technical achievements. His philosophical reflections on the nature of mathematical discovery have shaped how we teach and learn mathematics, emphasizing the role of intuition and creativity in problem-solving. As we continue to explore the frontiers of science and technology, Hadamard’s ideas remain a guiding light, reminding us of the deep connections between abstract theory and real-world innovation.
"Mathematics is not a careful march down a well-cleared highway, but a journey into a strange wilderness, where the explorers often get lost. Rigor should be a signal to the historian that the maps have been made, and the real explorers have gone elsewhere." — W.S. Anglin, echoing Hadamard’s spirit
In an era defined by rapid technological advancement, Hadamard’s contributions serve as a foundation for future breakthroughs. Whether in the development of quantum algorithms, the optimization of machine learning models, or the exploration of number theory’s deepest mysteries, his work continues to inspire and challenge mathematicians and scientists alike. As we stand on the shoulders of this giant, we are reminded that the pursuit of knowledge is a journey—one that Hadamard navigated with unparalleled brilliance and vision.
Decoding the H-Symbol: Mathematics, Physics, and Greek Heritage
The intriguing phrase "H-Symbol of Emy Neter in Mathematics and Physics" opens a fascinating gateway into interdisciplinary exploration. While not a standard term in academic lexicons, it invites an investigation into symbolic language, historical figures, and cultural intersections within the sciences. This article will unravel the most plausible interpretations, anchoring them in the rich contexts of Greek educational frameworks and global scientific discourse. Our journey connects potential meanings, from iconic mathematical operators to transformative historical legacies.
Understanding this topic requires navigating both precise scientific terminology and broader cultural narratives. The Greek educational system provides a crucial backdrop, with its structured emphasis on mathematics and physics shaping public engagement with these fields. Recent trends show a growing interest in programs that blend scientific rigor with philosophical and historical inquiry, particularly within Greece itself.
Interpreting the Core Phrase: A Multifaceted Puzzle
The initial challenge lies in decoding the original string. It appears to be a romanized version of a potential Greek title. Several key interpretations emerge from careful analysis, each leading down a distinct yet enlightening path. These paths converge on the enduring human quest to use symbols and names to explain the fundamental laws of nature.
The Mathematical and Physical "H-Symbol"
In formal science, the letter H often denotes pivotal concepts. In physics, it universally represents the Hamiltonian operator, the cornerstone of classical and quantum mechanics that encapsulates a system's total energy. In mathematics, H appears in various contexts, from Hecke operators in number theory to the Hilbert space in functional analysis.
However, no widely recognized "H-Symbol of Emy Neter" exists in indexed literature. This absence suggests the phrase may be a creative or localized title rather than a technical term. It could symbolize a conceptual bridge or a personalized pedagogical tool within a specific educational or cultural project.
The Emmy Noether Hypothesis: A Likely Candidate
The most compelling and educationally significant interpretation involves a probable transliteration error. The name "Emy Neter" strongly resembles "Emmy Noether," the legendary German mathematician. Emmy Noether's groundbreaking theorems fundamentally linked symmetry principles to conservation laws in physics, a concept central to modern theoretical physics.
If the intended subject is "The Significance of Emmy Noether in Mathematics and Physics," the topic is profoundly rich. Noether's work is a pillar of contemporary science, making this hypothesis highly plausible for any discussion seeking to connect deep mathematical ideas to physical law.
Noether's theorem is often described as one of the most important mathematical results in theoretical physics, guiding everything from classical mechanics to quantum field theory.
The Ancient Egyptian "Neter" Interpretation
Alternatively, "Neter" could reference the ancient Egyptian term "nṯr" (neter/netjer), meaning a divine force or god. This opens an interdisciplinary, cultural lens. A phrase combining "neter" with Greek words for mathematics and physics might explore the historical personification of natural forces or the philosophical origins of scientific thought.
Such a theme aligns with modern interdisciplinary programs in Greece and globally that examine the history and philosophy of science. This interpretation, while not mainstream science, reflects a growing academic interest in the cultural roots of scientific inquiry.
The Greek Educational Context: A Foundation for Inquiry
To fully appreciate where such a topic might emerge, one must understand its potential incubator. The Greek education system maintains a strong, structured focus on the core sciences, creating an audience keenly interested in the intersections of mathematics, physics, and culture.
Curriculum Emphasis on Core Sciences
In Greek upper secondary education, the teaching hours dedicated to mathematics and physics are substantial and vary by student specialization. This structured exposure cultivates a foundational literacy in these subjects among a significant portion of the population.
- Mathematics can be allocated from 3 to 6 hours weekly depending on the student's academic track.
- Physics typically receives around 2 hours per week in general programs, increasing significantly in science-focused specializations.
This curricular emphasis ensures that topics blending mathematical rigor and physical principles resonate within the Greek educational landscape. It provides a ready audience for discussions that extend beyond pure textbook formulas into historical and philosophical dimensions.
Trends in Greek Higher Education and Events
The Greek academic scene actively fosters cross-disciplinary dialogue. Recent years have seen a proliferation of conferences, summer schools, and workshops that intentionally bridge STEM fields with the humanities, history, and philosophy.
For instance, events like the PHYSIS Summer School explicitly explore the connections between ancient conceptions of nature and modern science. Such programs demonstrate an institutional environment where a title mixing Greek language, symbolic concepts, and scientific themes would be perfectly at home.
- Specialized conferences on physics and mathematics are regularly hosted in Greece.
- University courses explore themes like "Math and Physics of the Ancient World."
- There is a noted increase in public outreach and popularization of complex scientific ideas.
These trends create a fertile ground for the kind of nuanced exploration suggested by our core phrase. They indicate that the discussion is not happening in a vacuum but within a vibrant, engaged intellectual community.
Emmy Noether: The Probable Mathematical and Physical Keystone
If "Emy Neter" is indeed a reference to Emmy Noether, then the discussion enters the realm of foundational scientific legacy. Noether's theorem represents one of the most profound connections between abstract mathematics and tangible physical law. Her work demonstrated that every differentiable symmetry of a physical system corresponds to a conservation law.
This principle is a cornerstone of modern theoretical physics. It directly links, for example, the symmetry of time translation to the conservation of energy. Her innovations in abstract algebra also reshaped mathematics, establishing her as a towering figure whose influence permeates both disciplines. Exploring her significance provides a clear, impactful narrative for the original phrase.
Noether's Theorem and Its Universal Applications
The power of Noether's theorem lies in its universal applicability. From classical mechanics, where it explains the conservation of momentum, to quantum field theory and the Standard Model of particle physics, her insight is indispensable. The theorem provides a critical tool for physicists to derive conserved quantities directly from the observed symmetries of a system.
This deep interconnection means that studying symmetry is not merely an aesthetic or mathematical exercise. It is a direct pipeline to understanding the fundamental constants and rules governing the universe. The theorem is a mandatory component of advanced physics curricula worldwide, underscoring its non-negotiable importance.
Albert Einstein described Emmy Noether as "the most significant creative mathematical genius thus far produced since the higher education of women began."
Overcoming Barriers: Noether's Legacy in Science History
Noether's story is also one of perseverance against significant institutional barriers. As a woman in early 20th-century academia, she faced immense challenges in gaining recognition and a formal position. Her work was initially undervalued, yet its sheer intellectual force eventually made it impossible to ignore.
Her legacy today is twofold: she is celebrated for her transformative scientific contributions and revered as an icon for women in STEM. This dual significance makes her a highly relevant subject for contemporary educational discourse, particularly in discussions about inclusivity and recognizing hidden figures in science history.
- Pioneering Role: She paved the way for future generations of female mathematicians and physicists.
- Interdisciplinary Model: Her career exemplifies the fruitfulness of blending pure mathematics with theoretical physics.
- Modern Recognition: Institutions, awards, and scholarships now bear her name, solidifying her posthumous status.
The "H" as Hamiltonian: A Symbol of Dynamical Systems
If the "H-Symbol" is interpreted literally within physics, its most direct meaning is the Hamiltonian operator, denoted by H. In both classical and quantum mechanics, the Hamiltonian represents the total energy of a system—the sum of its kinetic and potential energies. This single symbol encodes the entire dynamics of a physical system.
Hamiltonian mechanics provides a powerful framework for analyzing complex systems, from planetary orbits to quantum states. The centrality of H in the fundamental equations of physics makes it one of the most important symbols in the scientific lexicon. Its utility extends into cutting-edge research, including chaos theory and quantum computing.
From Classical Orbits to Quantum States
In classical mechanics, the Hamiltonian formalism allows physicists to work with generalized coordinates and momenta. This approach simplifies solving problems involving constraints and complex motions. The equations derived from H provide a clear, symmetric path to understanding a system's evolution over time.
In quantum mechanics, the Hamiltonian takes on an even more crucial role. It becomes an operator whose eigenvalues correspond to the possible energy levels a system can occupy. Solving the time-independent Schrödinger equation, Hψ = Eψ, is the primary task for understanding atomic and subatomic structures.
- Classical: H = T + V (Kinetic + Potential Energy).
- Quantum: The Hamiltonian operator acts on the wavefunction ψ.
- Unifying Role: The concept bridges classical and modern physics seamlessly.
The H-Symbol in Contemporary Research Frontiers
The Hamiltonian framework is not a historical relic but a living tool. In quantum computing, designing Hamiltonians is essential for simulating complex molecules and materials. Researchers manipulate H to model chemical reactions and discover new properties of matter in ways impossible with classical computers alone.
Similarly, in condensed matter physics, topological phases of matter are classified using Hamiltonian analysis. The symbol H, therefore, sits at the very frontier of our understanding of the universe, from the infinitesimally small to the cosmological scale. Its enduring relevance underscores why a "symbol" can hold such immense conceptual weight.
Cultural and Historical Intersections: The "Neter" Pathway
The alternative interpretation, focusing on the ancient Egyptian concept of "neter," leads to a rich exploration of science's historical and philosophical roots. This path examines how early civilizations personified natural forces and sought to explain the cosmos through symbolic and divine frameworks, a precursor to later mathematical modeling.
This interdisciplinary angle connects the history of science, philosophy, and cultural studies. It asks how humanity's quest to understand nature evolved from mythological narratives to the quantitative, symbol-driven language of modern physics and mathematics. Such exploration is increasingly present in academic programs that value a holistic view of knowledge.
Ancient Cosmologies and the Language of Nature
Many ancient cultures, including the Egyptians, Greeks, and Mesopotamians, developed sophisticated cosmologies. They used symbolic language and personified deities (neteru) to describe the orderly principles they observed in the natural world—the movement of stars, the flooding of the Nile, or the cycle of life and death.
This symbolic representation was an early form of scientific modeling. While the methods differ radically, the underlying impulse—to find order and rule in nature—is the same driving force behind modern science. Studying these ancient systems can provide valuable historical context for the development of abstract thought.
The Greek educational system's recent interdisciplinary programs, such as those exploring "Math and Physics of the Ancient World," explicitly create space for this kind of comparative historical analysis.
Modern Re-engagement with Historical Concepts
Today, there is a renewed scholarly interest in how ancient knowledge systems can inform contemporary thinking. This is not about validating outdated science but about understanding the cognitive and cultural pathways that led to formal logic, geometry, and empirical investigation. The Greek word "φύσις" (physis), meaning "nature," is itself the root of "physics."
Programs and conferences in Greece and internationally are actively building these bridges. They examine, for instance, how Greek geometry and Egyptian practical mathematics converged and diverged. A phrase invoking "neter" in the context of math and physics could well be the title of a lecture or paper within such a forward-looking yet historically grounded forum.
- Summer schools like PHYSIS explore ancient and modern intersections.
- University courses examine historical scientific concepts critically.
- This re-engagement fosters a deeper appreciation for the evolution of scientific thought.
Synthesis and Convergence: The Power of Symbolic Language
The journey through the possible meanings of "H-Symbol of Emy Neter" reveals a common thread: the immense power of symbolic language in advancing human understanding. Whether through the precise operator H, the legacy of a genius like Noether, or the ancient symbolism of neter, humanity uses abstraction to grasp complex realities. This synthesis highlights the interdisciplinary nature of true scientific progress.
Mathematics and physics do not exist in a cultural vacuum. They are products of historical context, philosophical inquiry, and the relentless human drive to codify the universe. Recognizing this interconnectedness enriches our appreciation of both the sciences and the humanities. It demonstrates that symbols are bridges between intuition, observation, and formal proof.
The Role of Education in Fostering Interdisciplinary Thinking
The structure of the Greek educational system, with its balanced curriculum, provides a foundation for this kind of broad thinking. By allocating significant weekly hours to both mathematics and physics, it ensures students develop the necessary literacy to engage with complex ideas. Recent trends toward specialized summer schools and conferences further promote synthesis.
Programs that connect ancient philosophy with modern physics or explore the history of mathematical notation are directly cultivating this integrative mindset. They prepare students not just to calculate but to contextualize, which is a critical skill for the next generation of innovators and thinkers. This educational direction aligns with global movements toward STEM/STEAM integration.
- Curriculum Design: Greek secondary education provides a strong STEM base for interdisciplinary exploration.
- Higher Education Initiatives: Universities are launching courses that blend historical and modern scientific perspectives.
- Lifelong Learning: Public conferences and seminars make these syntheses accessible to a wider audience.
The Enduring Relevance of Emmy Noether's Contributions
Focusing on the most plausible interpretation, the significance of Emmy Noether cannot be overstated. Her work is a prime example of how pure mathematical insight can unlock fundamental truths about the physical world. Noether's theorem is more than a formula; it is a philosophical principle that symmetry and conservation are two faces of the same coin.
In today's research frontiers, from the search for new particles at the Large Hadron Collider to theoretical work on quantum gravity, Noether's principles remain actively used. They are foundational to the Standard Model of particle physics, where gauge symmetries dictate the forms of all fundamental interactions. This demonstrates the timeless applicability of her 20th-century breakthrough.
Noetherian Principles in Cutting-Edge Physics
Modern theoretical physics heavily relies on the framework established by Noether. The development of gauge theories, which describe the electromagnetic, weak, and strong nuclear forces, is deeply rooted in symmetry principles. Each force is associated with a specific symmetry, and the corresponding conserved quantities are derived directly from Noether's theorem.
Even in speculative areas like string theory and loop quantum gravity, the quest for underlying symmetries guides research. The theorem provides a reliable compass in the highly abstract landscape of theoretical physics. It ensures that new proposals remain grounded in the established conservation laws that have been experimentally verified for over a century.
"Noether's work permanently altered the landscape of theoretical physics and mathematics, proving that profound abstraction yields concrete physical predictions."
Greek Academic Landscape: A Hub for Future Explorations
Greece's contemporary academic scene is poised to be a fertile ground for discussions that mirror the ambiguous title we began with. The country's unique position—as the birthplace of Western science and philosophy and a modern EU member with a robust educational system—makes it an ideal host for fusion-oriented intellectual events.
The data shows a clear pattern of conferences, summer schools, and courses designed to break down disciplinary silos. This environment is precisely where a topic blending a symbolic "H," a historical figure ("Emy Neter"), and the hard sciences could naturally emerge and thrive.
Quantifying the Growth of Interdisciplinary Programs
Recent years have seen a measurable increase in cross-disciplinary offerings. For example, event listings show a significant number of physics and mathematics conferences scheduled in Greece for 2025-2026, many with themes connecting to history, philosophy, or education. These are not niche gatherings but established, respected academic venues.
Furthermore, analysis of university entry scores and subject preferences indicates a sustained student interest in the core sciences. This creates a pipeline of engaged minds ready to tackle complex, synthesized ideas. The infrastructure for deep, meaningful dialogue at the intersection of culture and science is actively being built and utilized.
- Conference Frequency: Multiple major interdisciplinary events are hosted in Greece annually.
- Student Engagement: Strong performance and interest in math/physics tracks at the secondary level.
- Institutional Support: Universities and research institutes are backing these hybrid initiatives.
Conclusion: Embracing Ambiguity as a Path to Insight
The exploration of the phrase "H-Symbol of Emy Neter in Mathematics and Physics" has taken us from technical definitions to historical biography and cultural analysis. This journey underscores a vital point: ambiguity in language can be a powerful catalyst for broader understanding. It forces us to consider multiple perspectives and uncover connections we might otherwise miss.
The most direct path likely leads to the monumental legacy of Emmy Noether and the Hamiltonian operator. This connection provides a rich, evidence-based narrative full of educational value and scientific importance. It highlights a key figure whose work is a cornerstone of modern theoretical physics and a testament to the power of abstract thought.
Key Takeaways for Scholars and Educators
Several crucial insights emerge from this investigation. First, the importance of precise terminology and historical context in scientific communication cannot be ignored. Second, the Greek educational framework is actively supporting the kind of interdisciplinary thinking that makes such explorations possible. Finally, the enduring relevance of foundational ideas, whether from the early 20th century or ancient civilizations, continues to shape contemporary inquiry.
Educators can use this multifaceted topic as a case study in how science evolves. It shows how ideas travel, transform, and sometimes get rediscovered under new names. It demonstrates that the history of science is not a linear march but a rich tapestry woven from diverse threads of human curiosity.
A Compelling Vision for Integrated Knowledge
Ultimately, whether the original phrase was a transliteration error, a creative title, or a niche project name matters less than the discussion it generates. It points toward a future where scientific rigor and humanistic inquiry are not adversaries but partners. In a world facing complex global challenges, this integrated approach to knowledge is not just academically interesting—it is essential.
The next generation of problem-solvers will need to think symbolically, historically, and scientifically all at once. They must appreciate the Hamiltonian's elegance, understand Noether's struggle for recognition, and grasp how ancient civilizations sought patterns in nature. By embracing the full spectrum of meaning behind a simple string of words, we take a small but significant step toward that more holistic, and more human, understanding of our universe.

