Elliptic Curve Cryptography: Revolutionizing Digital Security

Introdução à Criptografia de Curvas Elípticas

A criptografia de curvas elípticas (ECC) é uma técnica avançada e eficiente decriptografia que está ganhando popularidade nas últimas décadas devido à sua robustez e eficiência comparada a outras formas de criptografia.

A criptografia moderna baseia-se em problemas matemáticos dificilmente resolvidos. Uma das estratégias mais bem sucedidas tem sido basear seus algoritmos em problemas de fatoração de números inteiros grandes ou sistemas de equações do segundo grau. Contudo, com o avanço tecnológico e em especial da computação quântica, essas técnicas começam a apresentar vulnerabilidades. É aqui que as curvas elípticas entram como uma alternativa promissora para garantir seguranças de comunicados digitais.

História e Desenvolvimento

A ideia de curvas elípticas pode remontar aos trabalhos de matemáticos do século XVIII, mas foi somente nos anos 1980 que se começou a explorar suas aplicações em criptografia. James Miller e Robert Koblitz foram os pioneiros nesse campo, propusemendo a ideia de usar curvas elípticas como base para criar sistemas de criptografia mais seguros e eficientes.

No início dos anos 1990, o National Institute of Standards and Technology (NIST) dos Estados Unidos lançou padrões recomendados para o uso de curvas elípticas em criptografia. Desde então, diversas organizações governamentais e corporativas tem apoiado a adoção dessa tecnologia.

Especificidades Matemáticas das Curvas Elípticas

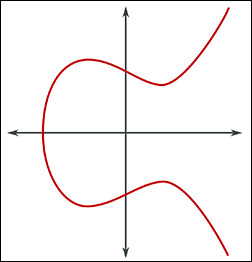
Uma curva elíptica é descrita por uma equação de forma geral dada por y² = x³ + ax + b, onde a e b são coeficientes definidos para determinar a forma específica da curva. Neste contexto, o conjunto de pontos que satisfazem a equação representa a curva elíptica.

A operação fundamental na criptografia de curvas elípticas é a Adição de Pontos sobre uma Curva Elíptica. Assim como a adição entre pontos em outras geometrias, a adição sobre uma curva elíptica envolve um procedimento geométrico baseado na interseção das retas através dos pontos. Por exemplo, dados dois pontos A e B em uma curva elíptica, a adição desses pontos resulta em outro ponto, C, que é simétrico à interseção da reta AB com a curva.

Esta operação, embora simplesmente vista geometricamente, tem aplicações profundas em criptografia. O que torna a criptografia de curvas elípticas especialmente segura é a dificuldade computacional em 'inversão' essa adição de pontos, ou seja, determinar os pontos iniciais à partir do resultado sem resolver o problema original.

Vantagens da Criptografia de Curvas Elípticas

O principal atrativo das curvas elípticas reside em sua eficiência relativamente alta. Isso significa que, usando as mesmas chaves de criptografia, curvas elípticas exigem menos bytes de dados ao passar por processos de criptografia e descriptografia comparados às criptografias mais tradicionais, como RSA.

Isso ocorre porque o tamanho da chave necessária para obter uma mesma segurança na criptografia de curva elíptica é significativamente menor. Por exemplo, uma chave de 256 bits em ECC oferece uma segurança equivalente a um algoritmo RSA de cerca de 3096 bits.

Aplicações Práticas

Em termos práticos, a ECC já é utilizada em grande escala em várias plataformas atualmente disponíveis no mercado, como sistemas de criptografia SSL/TLS, onde garantem que as comunicações entre servidores e clientes no Internet permaneçam privadas. Também é usada em sistemas de armazenamento seguro de autenticação digital em smartphones e computadores.

Além disso, muitas organizações financeiras e bancárias confiam na ECC para proteger suas transações financeiras. O processo de autenticação SSL/TLS é particularmente utilizado para garantir o acesso seguro aos serviços do cliente online.

Desafios e Considerações

A adição de ECC não vem sem desafios, principalmente no que diz respeito ao entendimento e implantação adequados de sua tecnologia. Não só é necessário um conhecimento sólido nesta área, mas também um cuidado detalhado ao gerenciar implementações para evitar vulnerabilidades.

A ECC ainda enfrenta resistência em algumas áreas por questões de compatibilidade com sistemas mais antigos que utilizam outros tipos de criptografia. Além disso, a falta de uma ampla adoção pode levar a diferenças nas implementações existentes, aumentando a probabilidade de inseguranças potenciais.

Outro ponto importante a considerar é que enquanto a ECC oferece segurança superior, ela também exige mais recursos computacionais para realizar operações de criptografia comparada às técnicas mais antigas. Esse fator pode ser problemático para dispositivos móveis com memória e processamento limitado.

Conclusão

A criptografia de curvas elípticas representa uma importante evolução na segurança digital proporcionando uma forma mais eficiente de criptografar informações críticas. Sua robustez contra computação quântica a torna uma ferramenta vital para a próxima geração de protocolos de criptografia.

Embora ainda enfrentem alguns desafios, as curvas elípticas estão rapidamente ganhando aceitação nos setores mais avançados de tecnologia. Com o crescente medo e cautela em torno da exposição de informações privadas na internet, ECC é uma solução viável e promissora para prevenir novas ameaças à segurança digital. Com seu potencial crescente e aplicação em diversos campos, é seguro dizer que as curvas elípticas continuarão sendo uma ferramenta crucial na defesa dos dados na era da informação moderna.

Tecnologias Atuais vs. Criptografia de Curvas Elípticas: Uso e Implementação

A comparação entre as soluções atuais de segurança em tecnologia e a criptografia de curvas elípticas (ECC) tem mostrado o quanto este último pode oferecer benefícios significativos. Ao analisarmos tanto em termos de desempenho quanto de segurança, as curvas elípticas emergem como uma opção superior por múltiplos motivos.

Em termos de uso, ECC já está sendo implementada em grande escala em várias plataformas de segurança digital. O uso de ECC não apenas garante maior velocidade de criptografia, mas também requer chaves menores para atingir níveis de segurança comparáveis às implementações convencionais. Isso resulta em menores exigências em termos de recursos computacionais, tornando-o mais viável para aplicativos e dispositivos móveis.

Ademais, ECC tem sido aplicado em várias indústrias como saúde, finanças, e serviços de comunicação. No âmbito médico, ECC é utilizado para criptografar dados de pacientes sensíveis. Nos bancos e instituições financeiras, esta tecnologia é essencial para proteger transações de pagamento e informações sobre conta.

A adoção da ECC é também relevante para redes Wi-Fi, onde a criptografia WPA2 e WPA3 incorporam ECC para aumentar a segurança das conexões. Essas implantações exemplificam como a criptografia de curvas elípticas pode ser integrada em diversos contextos para fornecer uma camada extra de segurança.

Análise Comparativa de Segurança

Para entender melhor por que ECC é preferível em comparação com outras técnicas de criptografia, uma análise comparativa das vulnerabilidades de cada sistema é necessária.

O Algoritmo RSA, por exemplo, depende de factores de números inteiros largos, onde a chave pública precisa de um número inteiro muito grande para se tornar praticamente indecifrável para um atacante. Entretanto, a implementação de computação quântica pode ameaçar a segurança desse sistema, pois uma máquina quântica poderia desfazer a criptografia em questão de minutos.

Já a criptografia de curvas elípticas encontra sua segurança na dificuldade de resolver equações elípticas em um campo finito. De acordo com experts de segurança cibernética, mesmo com a advenção de tecnologia quântica, ECC ainda oferece uma maior segurança devido à complexidade adicional que essas equações adicionam ao processo de criptografia.

Diferenças na Implementação

Implementar a criptografia de curvas elípticas pode parecer desafiador, principalmente para quem nunca antes trabalhou com essa técnica. No entanto, vários recursos e ferramentas já estão disponíveis para facilitar essa implementação.

O OpenSSL, um dos projetos mais populares do mundo de abrangência de software livres, oferece várias funções criptográficas, incluindo ECC. Outras ferramentas como BoringSSL e libgcrypt também permitem a integração da ECC em diferentes sistemas.

É importante lembrar que a correta configuração de uma implementação ECC depende de uma gestão segura da chave privada. Isso significa que qualquer aplicativo que use ECC deve ser rigorosamente testado para evitar vazamentos de informações.

Compatibilidade e Interoperabilidade

Com o aumento da adoção da ECC no mercado, é crucial que soluções antigos sejam compatíveis com esta nova tecnologia. Para mitigar problemas de incompatibilidade, organizações como NIST (National Institute of Standards and Technology) desenvolveram várias recomendações para garantir interoperabilidade.

Uma das principais recomendações é a utilização de curvas elípticas de nível seguro definido estaticamente. Curvas como P-256 (seu nome é derivado de seu tamanho de bit) são amplamente recomendadas para uso em redes onde a compatibilidade é essencial.

A comunidade de desenvolvedores tem contribuído enormemente para o progresso da ECC, disponibilizando uma variedade de libraries e frameworks em diferentes linguagens de programação que facilitam a integração desta tecnologia.

Nesta Era Quântica

A evolução da computação quântica representa um desafio significativo para todas as formas de criptografia existentes. Diferentemente do RSA e das chaves grandes necessárias, não há uma maneira conhecida de resolver problemas relacionados a curvas elípticas sem um despesa computacional excessiva.

Entretanto, mesmo diante de tais ameaças emergentes, as curvas elípticas ainda representam uma camada adicional de segurança valiosíssima. A capacidade intrínseca da ECC de resistir a ataques quânticos faz dela uma solução promissora para proteger dados em um futuro quântico.

Além disso, a comunidade científica e da segurança está trabalhando em desenvolvendo "quântica-resistantes" criptografias alternativas. Essas formas de criptografia, incluindo o Lattice-based Cryptography, podem se tornar uma alternativa para reforçar as defesas digitais contra ameaças quânticas. Contudo, a adoção desses métodos ainda está em estágios iniciais e a ECC continua sendo uma solução prática e segura atualmente.

Conclusão

A criptografia de curvas elípticas oferece uma solução promissora para melhorar a segurança digital, especialmente diante de avanços tecnológicos como a computação quântica. Sua eficiência e resistência única contra diversos tipos de ataques o tornam uma ferramenta valiosa para a proteção de dados em todos os níveis – desde dispositivos personais até sistemas financeiros de grande escala.

Maintendo-se atualizado sobre as melhores práticas e tendências da segurança cibernética, a implementação da criptografia de curvas elípticas pode trazer significativamente mais proteção para a informação digital que é tão vital em nossa sociedade moderna de alta tecnologia.

Mais Avanços e Futurismo

A tecnologia das curvas elípticas está longe de estar estagnada. Recentemente, pesquisadores e engenheiros continuam avançando, explorando novas caminhos e aplicativos para ECC. Um desses avanços é a implementação de ECC em blockchain, uma tecnologia emergente que utiliza criptografia extensivamente.

No âmbito da blockchain, ECC pode proporcionar uma solução versátil para a criação e verificação de assinaturas digitais. A integração eficiente de ECC pode permitir uma rede segura e confiável de transações de criptomoedas e outros ativos digitais. Além disso, a menor exigência de recursos computacionais facilita o uso da tecnologia em dispositivos com baixa potência, como smartphones e wearables.

Um outro cenário de futuro próximo para ECC é a Internet das Coisas (IoT), onde as pequenas quantidades de dados gerados pelos dispositivos demandam uma criptografia eficiente em termos de recursos. A ECC, graças à sua eficiência em termos de tamanho de chave, é ideal para esses ambientes restritos.

Necessidade de Melhorias Futuras

Embora as curvas elípticas ofereçam uma excelente tecnologia de criptografia, ainda há áreas onde podem ser melhoradas. Alguns desafios incluem questões de standardização global e educação da indústria de TI.

A standardização global é essencial para garantir que todas as implementações ECC sejam compatíveis e seguras. Em 2020, a NIST lançou uma chamada de comentários para um conjunto potencial de curvas elípticas para o uso em criptografia nacional de longo prazo. Este processo demonstra a necessidade de um consenso global e uma padronização rigorosa.

Educar a comunidade de TI sobre ECC é outro desafio. Muitos profissionais de segurança cibernética ainda não estão familiarizados com as nuances desta tecnologia. Workshops, palestras e tutoriais abertos podem ajudar a expandir essa capacidade dentro do setor.

Conclusão Final

A criptografia de curvas elípticas representa uma tecnologia revolucionária que está mudando o panorama da segurança digital em nosso mundo conectado. De sua robustez face aos ataques atualmente conhecidos até sua aplicação potencial em ambientes IoT e blockchain, ECC tem apresentado um desempenho notável desde o seu surgimento.

Embora ainda haja um longo caminho a percorrer para alcançar a plena adotação da ECC em todas as indústrias, a tecnologia parece mais sólida que nunca. Com contínuas inovações, a segurança que ECC proporciona continua sendo uma ferramenta crucial para protegermos nossos dados digitais.

À medida que a computação quântica se torna uma realidade cada vez mais próxima, a resistência da ECC a essas plataformas futuras só reforça o seu valor. Seja para a proteção de informações pessoais, transações financeiras, ou para impulsionar a tecnologia de blockchain, a criptografia de curvas elípticas continuará sendo uma peça-chave em nossa defesa digital.

Em resumo, as curvas elípticas são uma tecnologia que merece nossa atenção contínua. Sua eficiência, robustez e capacidade de adaptação garantem que a ECC será uma presença cada vez mais forte no cenário digital.

Criptografia de Chave Assimétrica: Segurança Digital Moderna

A criptografia de chave assimétrica, também chamada de criptografia de chave pública, é um pilar fundamental da segurança digital contemporânea. Ela utiliza um par de chaves matematicamente ligadas—uma pública e uma privada—para proteger informações sem exigir o compartilhamento prévio de um segredo. Este artigo explora profundamente como essa tecnologia revoluciona a proteção de dados na era da internet, eliminando vulnerabilidades críticas dos sistemas tradicionais.

O Que É Criptografia Assimétrica e Como Surgiu?

A criptografia de chave assimétrica resolve um problema histórico da criptografia: a troca segura da chave secreta. Diferentemente dos métodos simétricos, que usam uma única chave para cifrar e decifrar, a abordagem assimétrica emprega duas chaves distintas. A chave pública pode ser amplamente divulgada, enquanto a chave privada deve ser guardada com absoluto sigilo pelo seu proprietário.

Um Marco Histórico na Segurança da Informação

Este conceito revolucionário foi introduzido publicamente em 1976 por Whitfield Diffie e Martin Hellman. O trabalho deles, intitulado "New Directions in Cryptography", demonstrou pela primeira vez a possibilidade de comunicação segura através de canais inseguros sem necessidade de compartilhar uma chave secreta antecipadamente. Pouco depois, em 1977, o trio Rivest, Shamir e Adleman desenvolveu o algoritmo RSA, que se tornou a implementação prática mais famosa e popular da criptografia de chave pública, fundamentando-se na dificuldade de fatorar números primos grandes.

Funcionamento Básico: Chave Pública vs. Chave Privada

O cerne da criptografia assimétrica reside na relação matemática especial entre o par de chaves. Qualquer pessoa pode usar a chave pública de um destinatário para criptografar uma mensagem. No entanto, uma vez cifrada, apenas a chave privada correspondente, guardada exclusivamente pelo destinatário, pode descriptografar e ler o conteúdo original.

O Processo de Criptografia e Descriptografia

O processo envolve três passos principais. Primeiro, o remetente obtém a chave pública do destinatário, que está disponível em um diretório ou certificado digital. Em segundo lugar, ele utiliza essa chave pública para transformar a mensagem legível em um texto cifrado ilegível. Por fim, ao receber o texto cifrado, o destinatário aplica sua própria chave privada, mantida em segredo, para reverter o processo e acessar a informação original.

Qualquer pessoa usa a chave pública para criptografar mensagens, mas apenas o detentor da chave privada correspondente pode descriptografá-las.

Comparação Direta: Criptografia Assimétrica vs. Simétrica

Para entender a evolução, é essencial comparar a criptografia de chave assimétrica com seu antecessor, a criptografia simétrica. A simétrica, utilizada por milênios, se baseia em uma única chave secreta compartilhada entre as partes para cifrar e decifrar dados.

• Número de Chaves: Simétrica usa uma única chave secreta. Assimétrica usa um par de chaves (pública e privada).


• Segurança na Troca: A troca da chave única na simétrica é uma vulnerabilidade crítica. A assimétrica elimina esse problema, pois a chave pública pode viajar abertamente.


• Velocidade e Eficiência: Algoritmos simétricos são mais rápidos e consomem menos recursos computacionais. Os algoritmos assimétricos são matematicamente mais complexos e, portanto, mais lentos.

Esta diferença de desempenho levou ao desenvolvimento do modelo híbrido, predominante hoje, que combina os pontos fortes de ambas as tecnologias.

Algoritmos Fundamentais: RSA e Diffie-Hellman

Dois algoritmos formam a base da maioria das implementações de criptografia de chave pública. Compreendê-los é chave para entender a segurança digital atual.

RSA: A Base na Fatoração de Primos

O algoritmo RSA, batizado com as iniciais de seus criadores (Rivest, Shamir, Adleman), fundamenta sua segurança na dificuldade prática de fatorar o produto de dois números primos muito grandes. A chave pública consiste nesse produto e em um expoente, enquanto a chave privada contém os primos originais. Acredita-se que, com a tecnologia atual, quebrar um RSA de 2048 bits por fatoração levaria bilhões de anos.

Diffie-Hellman: A Troca Segura de Chaves

O protocolo Diffie-Hellman (D-H), criado pelos próprios pioneiros do conceito, resolve especificamente o problema da troca segura de chaves em canais não seguros. Dois participantes podem, trocando informações públicas, derivar um segredo compartilhado que será conhecido apenas por eles. Esse segresso pode então ser usado como uma chave simétrica para uma sessão de comunicação rápida.

Aplicações Ubíquas na Internet Moderna

A criptografia de chave assimétrica não é apenas teoria; é a tecnologia invisível que protege a maior parte das nossas interações online. Sua adoção é maciça e essencial para a infraestrutura global de comunicação.

Uma de suas aplicações mais visíveis é o protocolo TLS/SSL, representado pelo cadeado ao lado da URL do navegador. Ele utiliza criptografia assimétrica durante o handshake inicial para autenticar servidores e estabelecer com segurança uma chave de sessão simétrica. Estima-se que o TLS proteja mais de 95% do tráfego web global em conexões HTTPS.

Principais Casos de Uso

• Certificados Digitais e HTTPS: Autenticam a identidade de sites e habilitam conexões criptografadas.


• Assinaturas Digitais: Garantem a autenticidade e a integridade de documentos e softwares, utilizando a lógica inversa (criptografa-se com a chave privada para verificar com a pública).


• Criptografia de E-mail (ex.: PGP): Protege o conteúdo de mensagens de correio eletrônico.


• VPNs e Redes Privadas: Estabelecem túneis seguros para acesso remoto e conectividade entre redes.


• Blockchain e Criptomoedas: Gerenciam endereços e assinam transações de forma segura e verificável.

O Modelo Híbrido: A Fusão do Melhor de Duas Tecnologias

Para superar a lentidão inerente aos algoritmos assimétricos, o mundo digital adotou amplamente um modelo híbrido inteligente. Este modelo aproveita a segurança da criptografia de chave assimétrica para iniciar a comunicação e trocar segredos, e então emprega a velocidade da criptografia simétrica para o restante da sessão. É o melhor dos dois mundos em ação.

O Handshake TLS: Um Exemplo Prático Perfeito

Quando você acessa um site seguro (HTTPS), seu navegador inicia um processo chamado handshake TLS. Nele, a comunicação começa com criptografia assimétrica: o navegador verifica o certificado digital do servidor (que contém sua chave pública) e usa essa chave para criptografar um segredo. Apenas o servivo com a chave privada correspondente pode descriptografar. Esse segredo então é usado para derivar uma chave de sessão simétrica, que será usada para criptografar toda a comunicação subsequente de forma ágil. Esta abordagem é responsável por processar bilhões de transações diárias de e-commerce e banking online com segurança e eficiência.

Segurança Matemática: Por Que É Difícil Quebrar?

A robustez da criptografia de chave assimétrica não reside no segredo do algoritmo, que é público, mas na complexidade matemática de problemas subjacentes. A segurança é baseada em operações que são fáceis de fazer em uma direção, mas extremamente difíceis de reverter sem informações específicas.

Os Problemas Matemáticos por Trás dos Algoritmos

Diferentes algoritmos exploram diferentes problemas matemáticos considerados computacionalmente intratáveis com a tecnologia atual.

• RSA (Fatoração de Inteiros): Baseia-se na dificuldade de fatorar um número grande que é produto de dois números primos grandes. Apesar de saber a chave pública (o produto), deduzir os primos originais para obter a chave privada é um problema de complexidade exponencial.


• Diffie-Hellman (Problema do Logaritmo Discreto): Baseia-se na dificuldade de calcular logaritmos discretos dentro de grupos algébricos. Mesmo conhecendo os valores trocados publicamente, é inviável computar o segredo compartilhado sem uma das chaves privadas.


• Criptografia de Curvas Elípticas (ECC): Uma evolução mais moderna que usa o problema do logaritmo discreto em grupos de curvas elípticas. Oferece níveis de segurança equivalentes ao RSA com chaves muito menores, sendo mais eficiente.

A segurança da criptografia assimétrica depende de problemas matemáticos fáceis de verificar, mas difíceis de resolver sem a informação secreta (a chave privada).

Vantagens e Desvantagens da Criptografia Assimétrica

Como qualquer tecnologia, a criptografia de chave pública apresenta um conjunto de pontos fortes e fracos que definem seu uso ideal. Entendê-los é crucial para projetar sistemas seguros.

Principais Vantagens

As vantagens são os motivos pelos quais essa tecnologia se tornou onipresente na segurança digital.

• Eliminação da Troca Segura de Chaves: Seu maior benefício. Não há necessidade de um canal seguro para trocar uma chave secreta inicial, resolvendo um enorme problema de logística e segurança.


• Escalabilidade em Comunicações Múltiplas: Para se comunicar com milhares de pessoas, você só precisa guardar uma única chave privada. Cada pessoa usa sua chave pública, que é livremente distribuída.


• Facilita a Autenticação e Assinaturas Digitais: Permite provar a identidade e a integridade de dados através de assinaturas digitais, um recurso impossível com criptografia simétrica pura.


• Não-Repúdio: Como apenas o detentor da chave privada pode gerar uma assinatura digital válida para seus dados, ele não pode negar posteriormente a autoria (não-repúdio).

Desafios e Desvantagens

Esses desafios são a razão pela qual o modelo híbrido com criptografia simétrica é quase sempre utilizado.

• Velocidade e Desempenho: Os algoritmos assimétricos são significativamente mais lentos (da ordem de 100 a 1000 vezes) e consomem mais poder de processamento do que os algoritmos simétricos para a mesma quantidade de dados.


• Tamanho Maior das Chaves: Para um nível de segurança equivalente, as chaves assimétricas são muito maiores. Por exemplo, uma chave RSA de 2048 bits oferece segurança similar a uma chave simétrica de 112 bits.


• Gerenciamento e Confiança em Chaves Públicas: Surge o problema de como garantir que uma chave pública realmente pertence à pessoa ou entidade que diz ser. Isso é resolvido por uma Infraestrutura de Chaves Públicas (ICP ou PKI) e certificados digitais emitidos por autoridades confiáveis.


• Ameaças Futuras (Computação Quântica): Algoritmos como RSA e Diffie-Hellman são vulneráveis a ataques de computadores quânticos suficientemente poderosos, que poderiam quebrá-los usando o algoritmo de Shor.

A Infraestrutura de Chaves Públicas (ICP/PKI)

Para que a criptografia de chave assimétrica funcione em escala global com confiança, é necessária uma infraestrutura que gerencie a autenticidade das chaves públicas. Essa é a função da Infraestrutura de Chaves Públicas (ICP ou PKI). Ela fornece um framework que vincula uma chave pública a uma identidade através de um documento digital chamado certificado digital.

Componentes Essenciais da ICP

A ICP é um ecossistema composto por várias entidades e processos interligados.

• Autoridade Certificadora (AC): A entidade confiável que emite, revoga e gerencia os certificados digitais. Ela "assina" digitalmente os certificados, atestando que a chave pública dentro dele pertence à entidade listada.


• Certificado Digital: Um documento eletrônico que associa uma chave pública a uma identidade (pessoa, servidor, empresa). Contém informações como o nome do titular, a chave pública, a AC emissora, data de validade e sua assinatura digital.


• Autoridade de Registro (AR): Responsável por verificar a identidade do solicitante antes de a AC emitir um certificado.


• Lista de Certificados Revogados (LCR ou CRL): Uma lista mantida pela AC de certificados que foram cancelados antes de sua data de expiração, seja por perda da chave privada ou suspeita de comprometimento.

Como o Navegador Confia em um Site?

Quando você visita um site HTTPS, seu navegador recebe o certificado digital do servidor. Ele então verifica: se a assinatura da AC é válida, se o certificado está dentro do prazo de validade, e se não está na lista de revogados. Para isso, o navegador já possui uma lista pré-instalada de ACs Raiz confiáveis. Essa cadeia de confiança, da AC Raiz até o certificado do site, é o que permite a autenticação segura na web. Estima-se que 100% das conexões HTTPS dependam deste mecanismo para estabelecer confiança inicial usando criptografia assimétrica.

Criptografia Pós-Quântica: O Desafio do Futuro

O advento da computação quântica representa o maior desafio teórico para os algoritmos de criptografia de chave assimétrica atualmente dominantes. Computadores quânticos, aproveitando-se de princípios da física quântica como a superposição e o emaranhamento, poderão um dia executar algoritmos capazes de quebrar os problemas matemáticos que garantem a segurança do RSA e do Diffie-Hellman em tempo viável.

A Ameaça do Algoritmo de Shor

Em particular, o algoritmo de Shor, formulado em 1994, demonstra que um computador quântico suficientemente poderoso poderia fatorar números inteiros grandes e resolver logaritmos discretos com eficiência exponencial. Isso tornaria obsoletos os sistemas baseados nesses problemas, comprometendo a segurança de praticamente toda a infraestrutura digital atual. Apesar de um computador quântico prático para essa tarefa ainda não existir, a preparação para esta transição já começou.

A Corrida pela Padronização e os Novos Algoritmos

Diante dessa ameaça futura, agências como o Instituto Nacional de Padrões e Tecnologia dos EUA (NIST) lideram uma iniciativa global para padronizar algoritmos de criptografia pós-quântica (PQC). Estes novos algoritmos são projetados para serem seguros tanto contra ataques de computadores clássicos quanto quânticos. Em 2024, o NIST concluiu um processo de vários anos, selecionando o algoritmo CRYSTALS-Kyber para criptografia de chave pública e outros para assinaturas digitais.

A transição para a criptografia pós-quântica é uma jornada de anos, necessitando da atualização de bilhões de dispositivos e sistemas em todo o mundo para manter a segurança a longo prazo.

Aplicações em Expansão: Além da Web Segura

Enquanto se prepara para o futuro quântico, a criptografia assimétrica continua a expandir seu domínio de aplicações. Sua capacidade de fornecer autenticação, não-repúdio e estabelecimento seguro de chave é fundamental para tecnologias emergentes.

Internet das Coisas (IoT) e Dispositivos Conectados

O mundo da Internet das Coisas, com bilhões de sensores e dispositivos conectados, enfrenta desafios únicos de segurança. A criptografia de chave pública é vital para provisionar seguramente esses dispositivos, autenticá-los em redes e garantir que as atualizações de firmware sejam legítimas e não comprometidas. Protocolos leves baseados em Curvas Elípticas (ECC) são frequentemente preferidos devido ao seu menor consumo de energia e tamanho de chave reduzido.

Blockchain e Criptomoedas

Tecnologias de blockchain, como Bitcoin e Ethereum, dependem intrinsicamente da criptografia assimétrica. Endereços públicos em uma blockchain são derivados de chaves públicas, enquanto as transações são assinadas digitalmente com as chaves privadas correspondentes. Este mecanismo garante que apenas o proprietário dos fundos possa autorizar sua transferência, proporcionando um sistema de propriedade e transferência de valor sem necessidade de um intermediário central confiável.

Criptografia de E-mail (PGP/GPG) e Mensagens

Protocolos como PGP (Pretty Good Privacy) e seu equivalente livre GPG (GNU Privacy Guard) utilizam criptografia assimétrica para proteger o conteúdo de e-mails e arquivos. Eles permitem que usuários troquem mensagens confidenciais e verifiquem a autenticidade do remetente em um ambiente tradicionalmente inseguro como o correio eletrônico.

Considerações de Implementação e Boas Práticas

Implementar criptografia de chave assimétrica de forma segura vai além de escolher um algoritmo. Requer atenção a detalhes críticos que, se negligenciados, podem comprometer todo o sistema.

Geração Segura de Chaves e Tamanho Adequado

A segurança começa com a geração segura do par de chaves. As chaves devem ser geradas em um ambiente confiável, utilizando geradores de números aleatórios criptograficamente seguros. O tamanho da chave é também um parâmetro crucial. Para o RSA, chaves de 2048 bits são consideradas o mínimo para segurança atual, com uma migração para 3072 ou 4096 bits para proteção de longo prazo. A ECC oferece segurança equivalente com chaves de apenas 256 bits.

Gestão do Ciclo de Vida das Chaves

Chaves não são eternas. Uma política de gestão do ciclo de vida deve definir sua rotação periódica (substituição), procedimentos para revogação em caso de suspeita de comprometimento, e destruição segura quando não forem mais necessárias. O uso de certificados digitais com datas de validade explícitas é uma prática padrão que força esta rotação.

Proteção da Chave Privada: O Santo Graal

Toda a segurança do sistema reside na proteção da chave privada. As melhores práticas incluem armazená-las em Hardware Security Modules (HSMs) – dispositivos físicos resistentes a adulteração –, usar cartões inteligentes ou tokens, e nunca embuti-las em código-fonte ou repositórios públicos. O acesso a elas deve ser estritamente controlado e auditado.

O Panorama Atual e o Caminho à Frente

A criptografia de chave assimétrica está profundamente entrelaçada com o tecido da sociedade digital. Sua evolução é constante, impulsionada por novas ameaças e pela expansão das fronteiras tecnológicas.

Hoje, ela opera majoritariamente de forma híbrida e invisível, protegendo silenciosamente nossas comunicações, transações financeiras e identidades digitais. Estima-se que, direta ou indiretamente, ela esteja envolvida na proteção de praticamente 100% do tráfego web seguro global e seja um componente crítico de protocolos de comunicação de última geração, como o 5G.

A Transição Contínua e a Conclusão

O futuro próximo será marcado por uma transição gradual para a criptografia pós-quântica. Esta migração será uma das maiores empreitadas de cibersegurança da história, exigindo a atualização coordenada de sistemas legados, bibliotecas criptográficas e padrões de protocolos em todo o mundo. No entanto, os princípios fundamentais estabelecidos pela criptografia de chave pública – autenticação, confidencialidade sem prévio compartilhamento de segredo, e não-repúdio – permanecerão mais relevantes do que nunca.

Conclusão: A Base Indispensável da Confiança Digital

A criptografia de chave assimétrica é, sem dúvida, uma das inovações mais transformadoras no campo da segurança da informação. Ao resolver elegantemente o dilema da distribuição de chaves, ela permitiu a construção da vasta infraestrutura de comércio, comunicação e serviços digitais que consideramos garantida hoje.

Desde sua concepção teórica nos anos 70 até sua implementação ubíqua em cada conexão HTTPS, sua jornada é um testemunho do poder da matemática aplicada. Ela nos ensina que a verdadeira segurança em um mundo conectado não depende do segredo absoluto, mas sim da gestão inteligente de segredos parciais e da verificação matemática da confiança. Enquanto navegamos para um futuro com computação quântica e bilhões de novos dispositivos conectados, os princípios e a evolução contínua da criptografia assimétrica continuarão a ser a pedra angular sobre a qual construiremos a próxima era da confiança digital.

Em conclusão, a criptografia assimétrica é essencial para a proteção de dados ao eliminar a necessidade de compartilhar um segredo prévio. Sua arquitetura de chave pública e privada garante a segurança de comunicações e transações digitais. Portanto, compreender esta tecnologia é fundamental para qualquer pessoa que interaja no mundo digital moderno.