Understanding the Diffie-Hellman Key Exchange: The Foundation of Secure Communications

In today's digital age, the need for secure communications has never been more critical. From banking transactions to personal messages, ensuring that information is exchanged securely is of paramount importance. The Diffie-Hellman Key Exchange, developed in the 1970s, stands out as one of the foundational protocols for enabling secure communication over open channels. But what exactly is it, and why is it so significant in the field of cryptography?

The Origins of Diffie-Hellman

Before delving into the technical aspects, it's essential to understand the historical context of the Diffie-Hellman Key Exchange. In 1976, two eminent cryptographers, Whitfield Diffie and Martin Hellman, introduced a groundbreaking method that allowed two parties to securely share a secret key over an insecure channel. This was revolutionary because, until then, secure communication typically required the exchange of keys through secure physical means. With the dawn of the internet, where such secure physical exchanges are often impossible, the Diffie-Hellman Key Exchange became an invaluable tool in ensuring the security of digital communications.

How Does Diffie-Hellman Work?

At its core, the Diffie-Hellman Key Exchange is a cryptographic protocol that allows two parties to generate a shared secret over an open network. This shared secret can then be used to encrypt subsequent communications, ensuring that only the intended recipients can read the messages.

Here's a simplified version of how the process works:

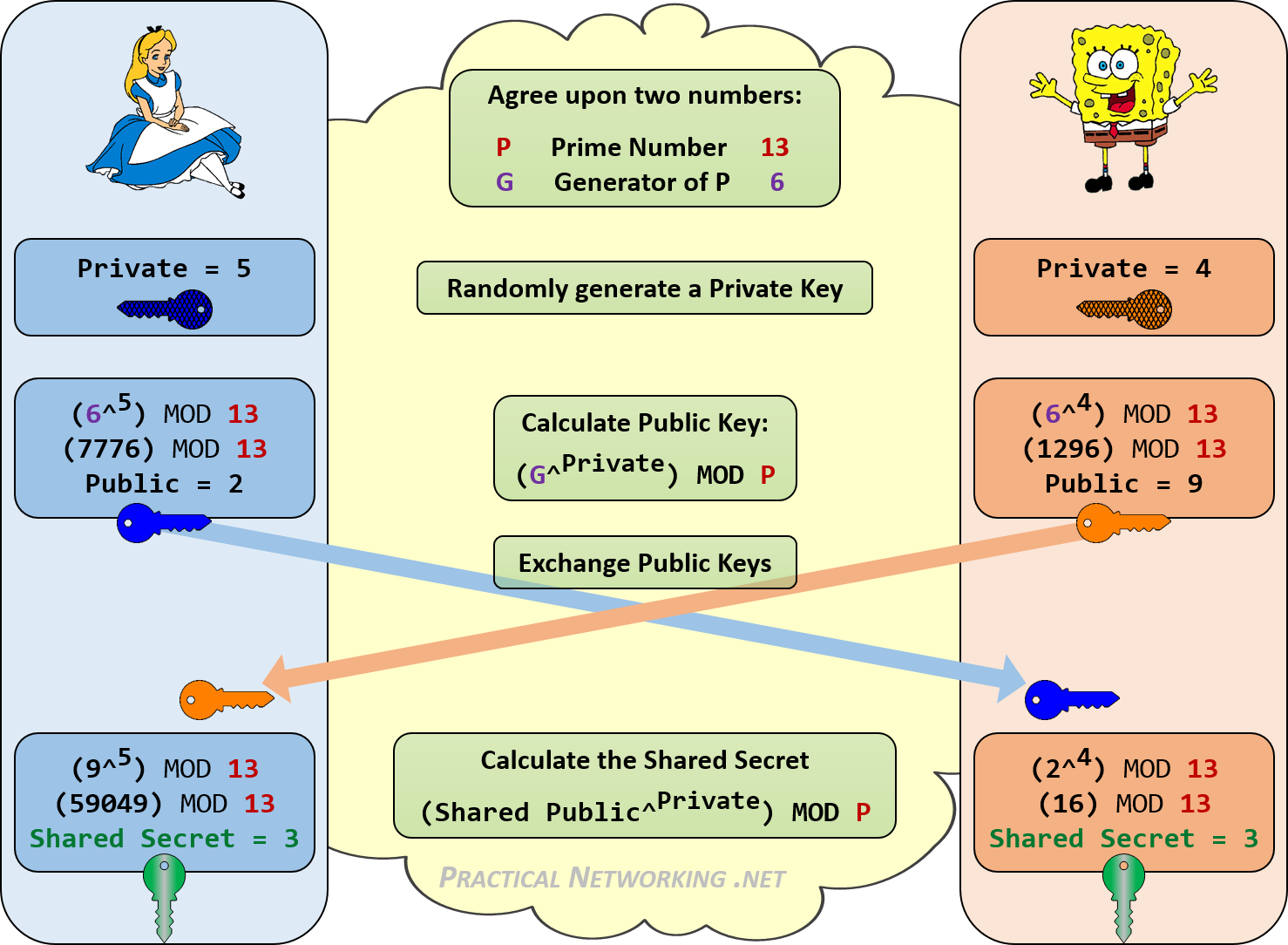
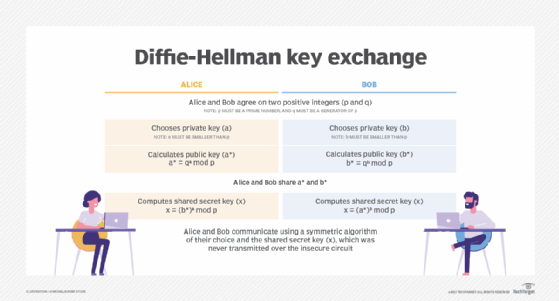
1. **Public Parameters Setup* Both parties agree on two numbers, a prime number \( p \) and a base \( g \), which are typically large and publicly shared. These numbers don't need to be secret but form the basis of the encryption process.

2. **Private Key Selection* Each party selects a private key. Let's call the private keys \( a \) for Alice and \( b \) for Bob. These keys are kept secret.

3. **Public Key Generation* Alice computes her public key as \( A = g^a \mod p \), and Bob computes \( B = g^b \mod p \). They exchange these public keys over the network.

4. **Shared Secret Computation* Using the received public key, each party computes the shared secret. Alice computes \( s = B^a \mod p \), and Bob computes \( s = A^b \mod p \). Surprisingly, both calculations result in the same value \( s \), which becomes their shared secret.

5. **Secure Communication* Once the shared secret is established, it can be used to encrypt communications using a symmetric key encryption algorithm.

Mathematics Behind the Magic

The security of the Diffie-Hellman Key Exchange is rooted in the difficulty of solving certain mathematical problems. Specifically, it's based on the difficulty of the Discrete Logarithm Problem. Given the numbers \( g^x \equiv A \mod p \), it's computationally hard to deduce \( x \) if \( p \) is large enough. This is what keeps the private keys secret, even if an attacker intercepts the public keys.

Applications of Diffie-Hellman

The Diffie-Hellman Key Exchange has vast applications, revolutionizing how secure communications are achieved:

1. **Secure Web Browsing* It’s used in the establishment of session keys for securing web traffic in protocols like HTTPS, ensuring that our browsing sessions remain private.

2. **VPNs and Secure Shell (SSH)* Many virtual private network (VPN) systems and SSH protocols use Diffie-Hellman for key exchange, providing users with a secure channel over potentially insecure networks.

3. **Wireless Security* Protocols like WPA2 in wireless networking use Diffie-Hellman for negotiating secure connections in wireless communications.

Limitations and Modern Adaptations

While revolutionary, the Diffie-Hellman Key Exchange isn't without limitations. Traditional implementations of Diffie-Hellman are vulnerable to certain types of attacks if not implemented correctly. For example, without authentication measures, the protocol is susceptible to 'man-in-the-middle' attacks. This means that an adversary can intercept and modify communications without the participants knowing.

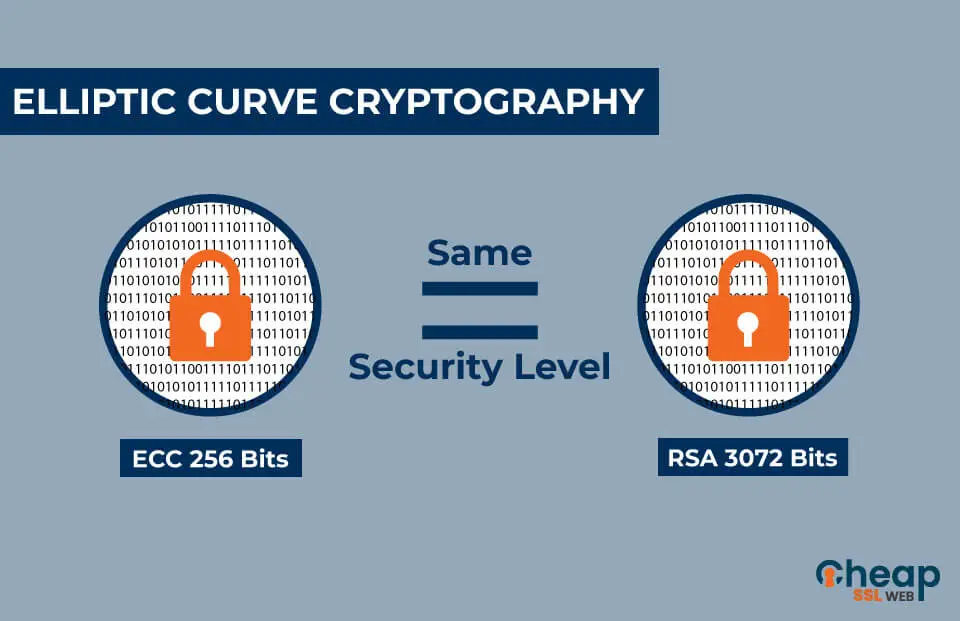
To counteract such vulnerabilities, modern protocols often combine Diffie-Hellman with authentication methods. The Diffie-Hellman algorithm itself has also seen advancements, such as the Elliptic Curve Diffie-Hellman (ECDH), which provides the same security level as traditional methods but with smaller keys, making it faster and more efficient.

The evolution and adaptation of the Diffie-Hellman Key Exchange continually highlight its importance in the cryptographic landscape. With increasing threats to digital security and the evolution of computational capabilities, ensuring that secure key exchange methods like Diffie-Hellman stay robust and effective is crucial for protecting private information in an interconnected world.

In summary, the Diffie-Hellman Key Exchange remains a cornerstone of modern cryptographic practices, allowing secure communication in an age where information is often under threat. As technology continues to evolve, so too will the methods we rely on to protect sensitive information. With a robust understanding of these foundational protocols, we not only appreciate their current applications but also the role they play in shaping the future of secure communications.

Enhancements and Variations of the Diffie-Hellman Protocol

As digital communications have evolved, so too have the variations and enhancements of the Diffie-Hellman Key Exchange in response to emerging security needs and technological advancements. One prominent adaptation is the development of the Elliptic Curve Diffie-Hellman (ECDH) protocol, which incorporates the mathematics of elliptic curves to provide even stronger security.

Elliptic Curve Diffie-Hellman (ECDH)

The ECDH protocol is a variant of the standard Diffie-Hellman Key Exchange that uses elliptic curve cryptography. The primary advantage of using elliptic curves is that they offer a higher degree of security with smaller key sizes, making them especially efficient for use in environments where computational power, storage, and bandwidth are limited. This makes ECDH a popular choice for mobile devices and IoT applications where resources are at a premium.

The appeal of elliptic curve cryptography lies in its reliance on the difficulty of solving the Elliptic Curve Discrete Logarithm Problem (ECDLP), analogous to the Discrete Logarithm Problem used in classical Diffie-Hellman. The ECDLP is believed to be a more complex problem, thereby making the cryptographic keys harder to break with the same length keys compared to the original method.

Authenticated Variants

To bolster the security of the basic Diffie-Hellman exchange, especially against man-in-the-middle attacks, authenticated versions have been developed. These enhanced protocols ensure that parties involved in a key exchange are indeed who they claim to be. Here are a few common methods:

1. **Station-to-Station (STS) Protocol* Designed to protect against adversaries attempting to impersonate legitimate users, the STS protocol incorporates signatures and encryption within the Diffie-Hellman exchange. Each party generates a digital signature of their key exchange message, which the other party can verify using previously established public keys.

2. **Digital Signatures and Certificates* By appending digital signatures and certificates to the messages exchanged in a Diffie-Hellman protocol, the communicating parties can verify each other's identities. Certificate authorities (CAs) play a critical role in this process by issuing digital certificates that bind public keys to individuals or organizations.

Quantum Computing and Future Threats

While Diffie-Hellman, including its elliptic curve variants, is robust against current computational threats, the advent of quantum computing poses potential challenges to existing cryptographic systems. Quantum computers, once fully realized, could solve problems like the Discrete Logarithm Problem in polynomial time, rendering traditional encryption methods vulnerable.

To counteract this future threat, researchers are working on quantum-resistant algorithms and protocols. Post-quantum cryptography aims to develop systems that can withstand the computational power of quantum computers, ensuring that secure communications remain feasible even in a quantum computing future.

Practical Implementation Challenges

Implementing the Diffie-Hellman Key Exchange, while theoretically straightforward, can encounter several practical challenges that need to be addressed to ensure effective security. These challenges include:

- **Parameter Selection* The security of the Diffie-Hellman Key Exchange is highly dependent on selecting appropriate parameters, including sufficiently large prime numbers and bases. Inadequate parameters can render the system susceptible to attacks.

- **Random Number Generation* The private keys selected by each party should be truly random to ensure security. The use of predictable or biased random number generators can undermine the cryptographic strength of the exchange.

- **Hardware Constraints* In environments with limited processing power or battery life, such as IoT devices and mobile phones, implementing robust cryptographic protocols like Diffie-Hellman efficiently is essential. This often necessitates a balance between security and performance.

The Significance of Perfect Forward Secrecy

An essential concept closely related to Diffie-Hellman implementations is Perfect Forward Secrecy (PFS). PFS ensures that even if the long-term private keys of a server are compromised, past session keys cannot be retrospectively decrypted. This feature is crucial for applications where long-term storage of encrypted data poses a security risk.

Diffie-Hellman, when used in key exchange methods that support PFS, guarantees that each session generates a new key, independent of previous sessions. Thus, even if an attacker manages to obtain the private key from a server, previous communications remain secure.

Real-World Applications and Impact

The widespread adoption and implementation of Diffie-Hellman Key Exchange protocols can be seen in myriad applications across different sectors:

1. **Secure Web Communications* As part of the Transport Layer Security (TLS) protocol, Diffie-Hellman ensures that secure web browsing remains a staple of internet usage, helping safeguard personal information in online transactions.

2. **Email Encryption* Protocols such as STARTTLS, used to secure email communications, leverage Diffie-Hellman to prevent eavesdropping and tampering.

3. **Secure Communications in Public Networks* Often used in applications like online banking and e-commerce, the Diffie-Hellman Key Exchange forms the bedrock for encrypting data during transactions over potentially insecure public networks.

As we continue to rely on digital platforms for every aspect of our lives, the importance of secure communication channels cannot be overstated. By leveraging protocols like Diffie-Hellman, organizations and individuals can ensure that their interactions over the internet remain private and authentic, protecting data from unauthorized access and misuse.

The legacy and evolution of the Diffie-Hellman Key Exchange highlight the dynamic nature of the cryptographic field. By understanding its principles and applications, we gain insight into the world of secure digital communications and the technologies that continue to safeguard our information in an increasingly connected world.

Diffie-Hellman in the Context of Modern Cryptographic Standards

As cryptographic standards have evolved to meet the needs of contemporary digital infrastructures, the Diffie-Hellman Key Exchange has maintained its relevance through inclusion in various security protocols and frameworks. Its integration into these standards illustrates its importance in ensuring privacy and security across the internet.

Integration in TLS/SSL Protocols

Transport Layer Security (TLS) and its predecessor, Secure Sockets Layer (SSL), are protocols that provide privacy and data integrity between two communicating computer applications. The Diffie-Hellman Key Exchange plays a crucial role in establishing secure connections, particularly during the handshake process. During a TLS handshake, the protocol ensures that both parties agree on the session keys used to encrypt data using Diffie-Hellman or its elliptic curve variant, ECDHE (Elliptic Curve Diffie-Hellman Ephemeral). The use of ephemeral keys (temporary keys that are never reused) enhances security further by contributing to Perfect Forward Secrecy, ensuring that past sessions remain secure even if current session keys are compromised.

Influence on Cryptographic Policies and Best Practices

Diffie-Hellman has also influenced cryptographic best practices adopted by organizations worldwide:

- **Key Length Recommendations* To maintain security standards, official guidelines such as those from the National Institute of Standards and Technology (NIST) recommend using keys of appropriate lengths to withstand attacks. For example, a minimum of 2048-bit key length is often suggested for the Diffie-Hellman algorithm to ensure robust security against current computational capabilities.

- **Associated Algorithms* Coupling Diffie-Hellman with robust encryption algorithms is a standard practice endorsed by cybersecurity experts. For instance, combining the key exchange with AES (Advanced Encryption Standard) ensures data integrity and confidentiality across various applications.

Assessing Security Vulnerabilities and Attack Vectors

While the Diffie-Hellman Key Exchange remains a cornerstone of cryptographic security, awareness of potential vulnerabilities is essential for effective implementation. Common attack vectors and potential vulnerabilities include:

- **Logjam Attack* This attack targets implementations that use smaller key sizes, exploiting weaknesses in export-grade Diffie-Hellman keys. It underscores the importance of using appropriately sized keys and staying updated with recommendations to mitigate threats.

- **Man-in-the-Middle Attacks* As mentioned earlier, without additional authentication measures, such as incorporating digital signatures or a Public Key Infrastructure (PKI), Diffie-Hellman exchanges might be vulnerable to interception by malicious actors. Ensuring proper authentication measures are in place is vital to prevent such exploits.

- **Side-Channel Attacks* These attacks exploit information about a system's physical implementation (like cache or timing data) to bypass cryptographic security. While not specific to Diffie-Hellman alone, mitigating these requires vigilance in guarding the physical and software aspects of cryptographic systems.

Staying Ahead of Technological Advances

Technological progress is relentless, and the cryptographic community continues to innovate to keep ahead of emerging threats. The Diffie-Hellman Key Exchange has shown remarkable adaptability, forming a basis for new methods and inspiring continued research and development.

Post-Quantum Cryptography

As mentioned earlier, one of the most pressing future challenges for Diffie-Hellman and other traditional cryptographic methods is the anticipated rise of quantum computing. Post-quantum cryptography aims to develop cryptosystems that can resist quantum attacks, and research is active in creating quantum-safe counterparts for current algorithms. Even in this transformative context, the principles introduced by Diffie-Hellman regarding secure key exchanges continue to be relevant as a basis for pioneering quantum-resistant protocols.

Ongoing Education and Cryptography Literacy

Another key factor ensuring that cryptographic systems remain robust is education and increased literacy in cryptography principles. As technologies evolve, staying informed about new developments helps developers and organizations implement the latest security measures efficiently. Regular audits, code reviews, and updates in line with cryptographic advancements are crucial for maintaining secure communications.

Conclusion: The Enduring Legacy of Diffie-Hellman

The Diffie-Hellman Key Exchange, with its ingenious approach to key exchange over insecure channels, has pioneered an era where secure digital communication is a fundamental expectation. Its ability to facilitate private conversations without requiring a pre-shared key revolutionized the approach to secure interactions in an online context.

Even as new challenges emerge, from enhanced computational capabilities to quantum threats, Diffie-Hellman's foundational contributions serve as a solid base that informs and inspires continuing innovation in cryptographic practices. The protocol's adaptability through variations like elliptic curve implementations and collaborations with authentication mechanisms illustrate its profound and lasting influence.

In an era where digital communication continues to expand exponentially, understanding and leveraging cryptographic concepts like Diffie-Hellman remain vital. By doing so, individuals and organizations harness the power of secure exchanges to protect private information, uphold privacy rights, and maintain the trust central to digital interactions. As this cornerstone of cryptography adapts to meet future security challenges, its legacy as a vital tool in safeguarding a complex, interconnected world endures.