Understanding Elliptic Curve Cryptography: A Modern Approach to Secure Communications

In today's rapidly evolving digital landscape, ensuring the security and integrity of data is paramount. As digital communication becomes more prevalent, so too does the necessity for robust encryption methods. Elliptic Curve Cryptography (ECC) stands out as a modern solution that not only provides reliable security but also does so with efficiency and elegance. This article delves into the intricacies of ECC, exploring its origins, mathematical foundations, and a few of its practical applications.

The Origins of Elliptic Curve Cryptography

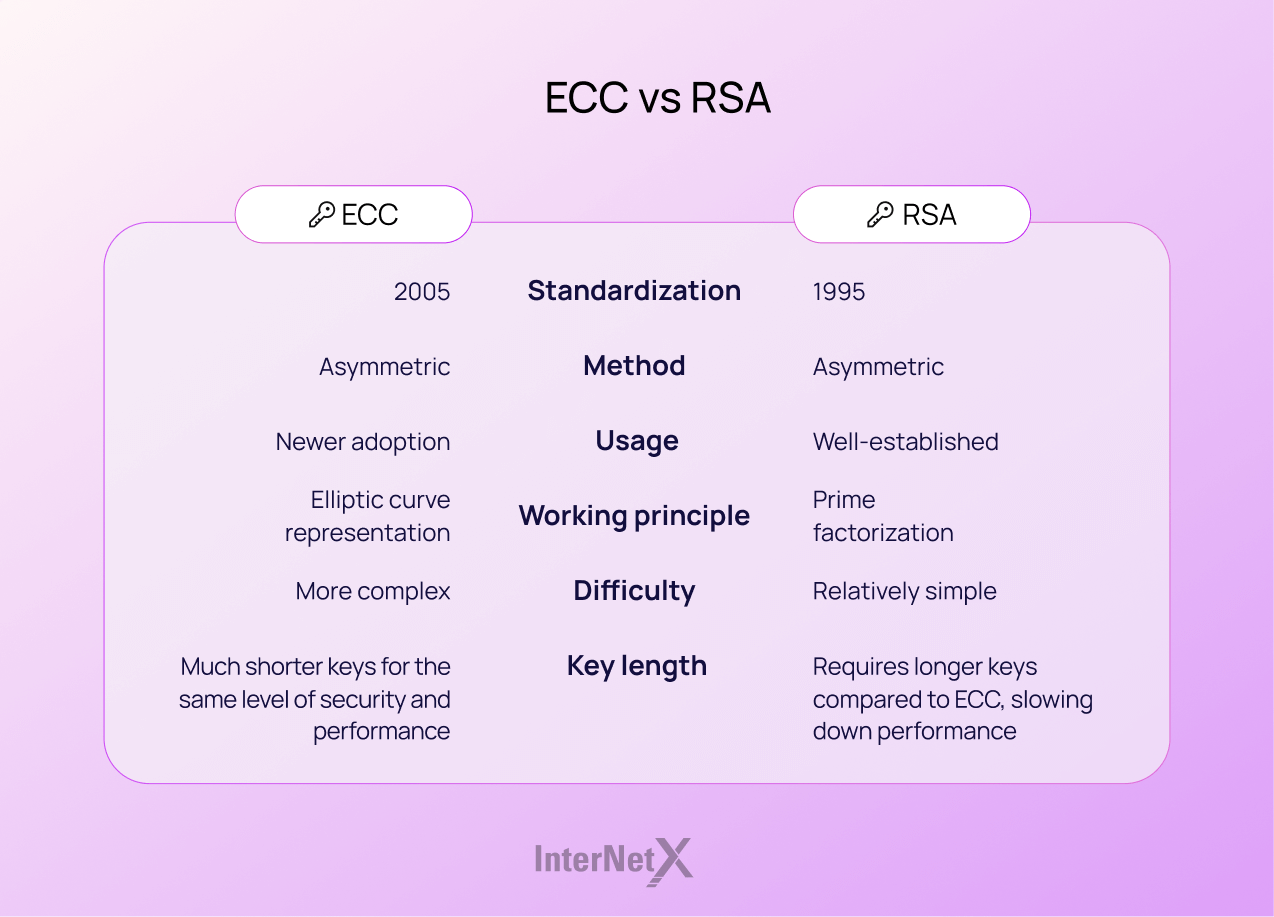
ECC is rooted in algebraic geometry, a branch of mathematics that studies geometric objects defined by polynomial equations. Introduced by Victor S. Miller and Neal Koblitz independently in the mid-1980s, ECC was designed as an alternative to traditional systems such as RSA and the Digital Signature Algorithm (DSA). What sets ECC apart is its unique use of elliptic curves, which offer a high level of security with relatively small keys compared to the large keys required by RSA for similar levels of protection.

This advancement came as a response to the increasing computational power that rendered many earlier cryptographic methods vulnerable to attack. ECC provides a way to maintain a high standard of security without necessitating unwieldy key sizes, making it particularly suitable for devices with limited computing resources, such as smartphones and IoT devices.

Understanding the Mathematics: What Are Elliptic Curves?

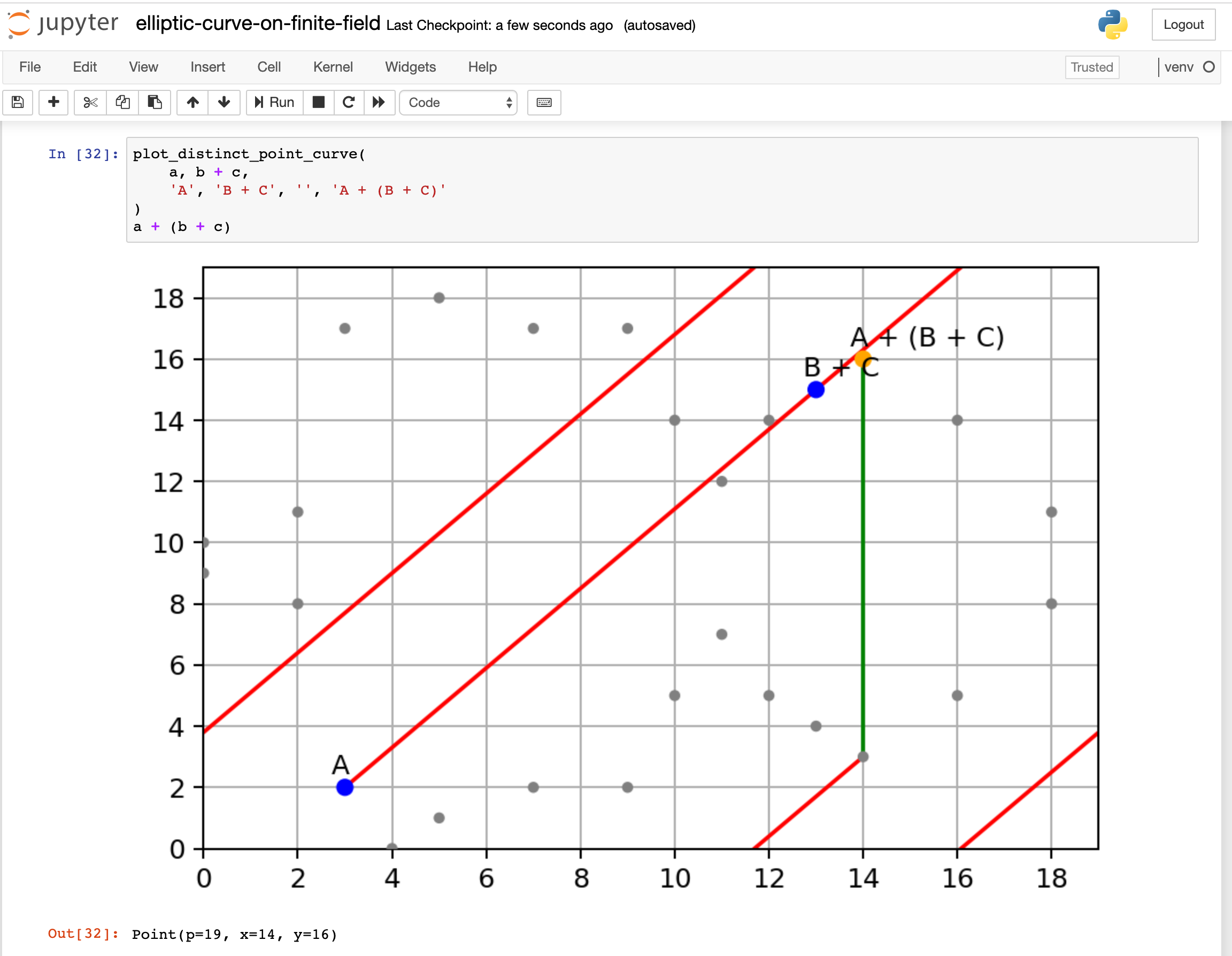
At the heart of ECC lies the mathematical concept of elliptic curves. An elliptic curve is defined by an equation of the form y^2 = x^3 + ax + b, where 4a^3 + 27b^2 ≠ 0 to ensure that the curve is non-singular. This equation describes a smooth, continuous curve without cusps or self-intersections.

One of the key properties of elliptic curves in the context of cryptography is the difficulty of the Elliptic Curve Discrete Logarithm Problem (ECDLP). The ECDLP asserts that given two points, P and Q, on an elliptic curve, it is computationally challenging to determine the integer k such that Q = kP. This one-way function is what provides the security foundation for ECC, making it exceedingly difficult for an adversary to deduce k without significant computational effort.

The operations performed on these elliptic curves, particularly point addition and scalar multiplication, are what enable encryption, decryption, and digital signatures. These operations lend ECC its efficiency, allowing it to achieve high levels of security with relatively small key lengths, a distinct advantage over traditional methods that require larger keys.

Advantages of ECC: Efficiency and Security

ECC's primary advantage lies in its efficiency. With shorter key lengths, ECC provides equivalent security to much longer keys used in other systems. For instance, a 256-bit key in ECC is considered as secure as a 3072-bit key in RSA. This considerable reduction in key length translates to faster computations and reduced power consumption, which is particularly beneficial for mobile and constrained environments.

Moreover, smaller keys simplify the management of cryptographic keys, as they require less storage space and bandwidth, thereby improving performance across networks. For organizations and developers, this means enhanced efficiency in deploying secure communications without compromising on security.

The enhanced security offered by ECC stems from the robust mathematical foundation of elliptic curves, which are resistant to many of the cryptanalytic attacks that threaten older systems. As computing power advances, the short key lengths of ECC remain resilient against brute-force attacks, providing a future-proof solution to securing digital communications.

Practical Applications of Elliptic Curve Cryptography

ECC has found widespread adoption across a variety of applications in both the private and public sectors. One notable use is in securing web transactions via Transport Layer Security (TLS). The adoption of ECC in the TLS protocol ensures secure communications between web browsers and servers, providing encryption to protect sensitive data like credit card numbers and personal information.

Additionally, ECC is used in cryptocurrency systems. Many digital currencies, including Bitcoin, utilize ECC to secure transactions and manage public keys. The compact nature of ECC keys is ideal for blockchain technology, which requires efficiency in processing and verifying vast numbers of transactions.

Another domain benefiting from ECC is mobile communications. Given the constrained processing power and battery life of mobile devices, ECC's efficient encryption allows for secure exchanges without taxing device resources.

Conclusion

Elliptic Curve Cryptography represents a significant advancement in the field of cryptography. Its blend of security and efficiency makes it a compelling choice for contemporary digital security needs. As we continue to rely more heavily on digital communications, the relevance of ECC will only grow, underpinning secure systems across the digital landscape. In the subsequent parts of this article, we will delve deeper into how ECC is implemented in real-world scenarios, examine its limitations and potential challenges, and explore ongoing advancements in elliptic curve research.

Diving Deeper: Implementation and Standards of ECC

Having explored the foundational principles and advantages of Elliptic Curve Cryptography, the implementation of ECC in real-world scenarios warrants closer inspection. The application of ECC extends beyond theoretical study and is governed by a series of standards that ensure uniformity and interoperability across various systems and platforms.

The most widely acknowledged standards for implementing ECC come from organizations such as the National Institute of Standards and Technology (NIST), the International Organization for Standardization (ISO), and the Internet Engineering Task Force (IETF). These bodies provide guidelines specifying the use of particular elliptic curves and parameters to foster secure and efficient encryption practices.

NIST Recommended Curves

NIST has curated a list of approved elliptic curves that are widely adopted across various cryptographic protocols. Some of the most common NIST curves include P-256, P-384, and P-521, where the numbers denote the bit length of the keys. These curves have been rigorously vetted for security, performance, and compatibility, making them standard choices for secure communications.

By providing a set of standardized curves, NIST ensures consistency in ECC implementations, allowing different cryptographic systems to interoperate. This standardization reduces the complexity of deploying ECC in various environments and mitigates the risk of vulnerabilities arising from incorrect implementation.

The Role of ECDH and ECDSA

Two key operations where ECC finds frequent use are the Elliptic-curve Diffie-Hellman (ECDH) key exchange and the Elliptic Curve Digital Signature Algorithm (ECDSA).

**ECDH** is a variant of the classic Diffie-Hellman cryptographic protocol but utilizes elliptic curves for shared key generation. ECDH enables two parties to generate a shared secret over an unsecured channel, which can subsequently be used to encrypt further communication. The efficiency of ECDH mirrors the overarching benefits of ECC, providing secure key exchange with reduced computational load.

**ECDSA**, on the other hand, leverages elliptic curves for digital signatures. It is similar to the Digital Signature Algorithm (DSA) but harnesses elliptic curve operations to achieve secure message verification with shorter keys. ECDSA is widely used in securing software updates, electronic signatures, and a plethora of other applications where authentication and data integrity are paramount.

Challenges and Limitations

While ECC offers numerous benefits, its implementation is not without challenges. One of the primary concerns is the proper generation and validation of elliptic curves. An incorrect curve choice or flawed implementation can undermine the security of an entire cryptographic system. This underscores the importance of adherence to established standards and guidelines when adopting ECC.

Moreover, ECC can be vulnerable to side-channel attacks, where an attacker attempts to extract private keys by analyzing information leaked during cryptographic operations. Techniques such as Differential Power Analysis (DPA) can exploit these vulnerabilities. To counteract such threats, implementers must employ side-channel resistant algorithms and architectures.

Another issue is patent-related concerns. Certain elliptic curve methods and implementations fall under intellectual property protections, requiring licenses for commercial use. Although many patents have expired or been resolved over the years, understanding the legal landscape remains crucial for developers and businesses looking to adopt ECC.

Ongoing Research and Future Directions

The field of elliptic curve cryptography is continuously evolving. Researchers aim to develop even more efficient algorithms and protocols to withstand future challenges, particularly in the context of evolving threats such as quantum computing. Quantum-resistant algorithms are a burgeoning area of exploration, as traditional ECC could potentially be vulnerable to quantum attacks. These new approaches, known as post-quantum cryptography (PQC), seek to devise security apparatuses that can resist the computational power of quantum computers.

Furthermore, advanced implementations like Pairing-Based Cryptography (PBC) are gaining traction. PBC extends ECC by using bilinear pairings on elliptic curves, facilitating new cryptographic primitives and applications such as identity-based encryption and attribute-based encryption, which offer innovative ways to enhance data security and access control.

Conclusion

Elliptic Curve Cryptography stands as a pivotal development in the realm of digital security, offering a blend of efficiency and robustness that is unmatched by many older cryptographic approaches. Yet, its implementation demands a careful balancing of standards adherence, security vigilance, and legal compliance. As technological advancements continue to shape the digital horizon, the role of ECC will adapt, maintaining its status as a cornerstone of secure communications globally. In the subsequent part of this article, we will further investigate ECC's impact on industries, discuss real-world case studies, and analyze its place in future technological innovations.

Real-World Impact and Industry Adoption of ECC

The adoption of Elliptic Curve Cryptography across various industries underscores its pivotal role in ensuring secure transactions and communications. From financial services to healthcare, ECC's influence is profound, driven by its ability to provide robust security efficiently.

Financial Services

The financial sector, with its high demands for confidentiality, integrity, and data authenticity, extensively leverages ECC. Banks and financial institutions employ ECC to secure online banking platforms, cryptocurrency transactions, and digital payments. The compact nature of ECC keys and the rapid computation times are particularly beneficial in enabling quick and secure financial transactions on mobile devices and point-of-sale systems.

For cryptocurrencies like Bitcoin and Ethereum, ECC is central to the management of keys and addressing. Bitcoin uses the secp256k1 curve for generating public keys and ensuring secure transactions. This reliance on ECC helps maintain the decentralized and secure nature of blockchain systems.

Healthcare Industry

In healthcare, the protection of sensitive patient data is paramount. ECC assists healthcare providers and enterprises in safeguarding data as it is transmitted between various electronic health records (EHR) systems and wearable health devices. By integrating ECC into medical data security frameworks, healthcare organizations achieve a balance between robust security mechanisms and minimal processing requirements, an essential feature given the growing volume of data generated.

Additionally, ECC supports the secure transfer of research data and intellectual property within the biotech and pharmaceutical industries, helping to protect against unauthorized access and cyber threats.

Telecommunications and IoT

The rise of the Internet of Things (IoT) poses unique security challenges due to the vast number of low-power, interconnected devices. ECC provides a feasible security framework for IoT, offering strong encryption capabilities while minimizing the computational load on devices with limited battery life and processing power.

Telecommunication companies use ECC to secure calls, messages, and data transfers. The global surge in mobile device usage necessitates encryption protocols that can maintain high levels of security without compromising performance, a niche where ECC excels.

ECC in Emerging Technologies

As industries evolve and digital transformation accelerates, ECC continues to adapt to emerging technologies and shifts in the landscape. One such area is cloud computing, where ECC ensures data encryption at rest and in transit across geographically dispersed data centers. Cloud service providers frequently employ ECC to maintain data privacy and security standards, allowing customers to leverage cloud resources confidently.

Moreover, ECC is exploring its potential within the scope of smart contracts and decentralized applications (dApps), enhancing the security and efficiency of automated, trustless agreements by ensuring that cryptographic operations remain secure and lightweight.

Evaluating ECC's Prospects: Challenges Ahead and Innovations

With ECC firmly entrenched in today's cryptographic applications, the focus now shifts to upcoming challenges and innovations that could shape its future. Quantum computing poses a significant existential threat to current cryptographic systems, with quantum algorithms such as Shor's algorithm capable of breaking traditional ECC.

Researchers and engineers are working on developing post-quantum cryptographic algorithms to preempt this threat. These new algorithms aim to preserve the cryptographic advantages of ECC while being resilient to quantum attacks, ensuring a secure foundation for future digital infrastructures.

Further advancements in ECC might involve the development of more efficient computational techniques and enhanced elliptic curve functions to extend its applicability and performance even further. These innovations are crucial not only for strengthening current applications but also for expanding ECC's role into uncharted realms.

Conclusion

Elliptic Curve Cryptography remains a cornerstone of modern encryption, a testament to its effectiveness in securing digital communications across diverse sectors. From financial institutions to the burgeoning IoT landscape, ECC's application demonstrates its versatility and potency. As the cryptographic community prepares for the post-quantum era, ECC's legacy will likely evolve, yet it will undoubtedly continue to influence the development of secure, efficient cryptographic solutions.

In summary, ECC's adoption reflects its capacity to address contemporary security challenges while promising adaptability for future advancements. As the global reliance on digital systems grows, the enduring relevance of ECC ensures it will remain at the forefront of cryptographic innovation, safeguarding the digital realm for years to come.