Jean-Baptiste Joseph Fourier: The Mathematical Pioneer of Thermal Analysis and Fourier Series
In the pantheon of scientific luminaries, few names resonate as fundamentally as that of Jean-Baptiste Joseph Fourier. An innovative mathematician and physicist hailing from France, Fourier's legacy rests predominantly on his groundbreaking work in the analysis of heat transfer and his development of Fourier Series, a mathematical tool with far-reaching implications across diverse scientific disciplines. This article seeks to provide an in-depth exploration of Fourier's life, his contributions to mathematics and science, and the enduring impact of his work.
Early Life and Education
Jean-Baptiste Joseph Fourier was born on March 21, 1768, in the quaint town of Auxerre, France. He was the ninth of twelve children in a humble family, with his father serving as a tailor. Tragically, Fourier's parents passed away when he was just a child, leaving him orphaned at the age of nine. Despite these adversities, Fourier's intellectual prowess and curiosity about the natural world shone through from an early age.
Fourier's formal education began at the military school in Auxerre, where he demonstrated a particular affinity for mathematics. His academic talents soon earned him admission to the prestigious École Royale Militaire of Auxerre, setting the stage for what would become a storied academic and scientific career. During his time there, Fourier developed a penchant for rigorous scientific inquiry, honing his skills under the tutelage of prominent mathematicians of the era.
Napoleonic Connection and Egypt Expedition
Fourier's mathematical genius caught the eye of General Napoléon Bonaparte, a connection that would profoundly influence the trajectory of his career. In 1798, Fourier joined Bonaparte's ambitious campaign to Egypt as a scientific advisor. The expedition aimed to study and document the historical and cultural treasures of the land alongside military operations. During his sojourn in Egypt, Fourier participated in numerous scientific endeavors, investigating the nation's geography and contributing to the documentation of its ancient monuments.
The Egyptian experience was transformative for Fourier, broadening his understanding of the world and providing a unique platform for intellectual exchange. It was during this period that Fourier began grappling with the scientific challenges that would ultimately define his legacy. His exposure to the diverse climate and its effects on ancient structures sparked a keen interest in the study of heat conduction, laying the groundwork for his future explorations.
The Groundbreaking Work on Heat Conduction
Upon returning to France, Fourier embarked on a research endeavor that would cement his place in scientific history. His seminal work, "Théorie Analytique de la Chaleur" (The Analytical Theory of Heat), published in 1822, revolutionized the study of thermal dynamics. Fourier's theory was built upon the premise that heat transfer could be analyzed through a process of decomposition into simpler mathematical functions, leading to the formulation of what we now know as Fourier Series.
Fourier's insight was profound: he proposed that any periodic function could be expressed as a sum of sine and cosine functions, each multiplied by a coefficient. This novel concept not only provided a powerful tool for analyzing heat conduction but also laid the foundation for the study of oscillatory behavior across a wide array of scientific phenomena.
Fourier Series in Modern Science
The implications of Fourier Series extended far beyond the realm of thermal analysis, permeating fields as varied as acoustics, optics, signal processing, and even quantum mechanics. Fourier's methodology for breaking down complex functions into their constituent frequencies underpins modern techniques for sound and image processing, enabling everything from audio compression in digital media to the intricate imaging systems used in medical diagnostics, such as MRI.
Furthermore, Fourier's work laid a crucial foundation for the development of modern telecommunications, providing the mathematical framework for encoding and transmitting information in today's interconnected world. Whether through the transmission of radio waves, the encryption of internet data, or the analysis of seismic waves, Fourier's insights form a cornerstone of our contemporary understanding of complex signal behavior.
Conclusion
Jean-Baptiste Joseph Fourier's contributions to science and mathematics are profound and enduring. His pioneering work opened new frontiers in the analysis of heat and created avenues of inquiry that continue to influence a myriad of technological advancements. Fourier's legacy is a testament to his intellectual curiosity, resilience, and unwavering dedication to scientific progress. As we continue to explore and expand upon the foundations he laid, his legacy endures, powering the engines of modern science and technology. The next part of this article will delve into further examinations of his influence and the continued relevance of his theories.
Fourier's Academic and Professional Journey
With his insights into the mathematics of heat transfer gaining traction, Jean-Baptiste Joseph Fourier's career took on a new dimension. Following his return from Egypt, he took up a position as a professor at the École Polytechnique in Paris, one of the foremost institutions for scientific study in France. His role at the École Polytechnique allowed him to delve deeper into his research while also influencing a new generation of mathematicians and scientists. The corridors of the institution buzzed with the excitement of new discoveries and ideas, with Fourier's presence adding invaluable breadth to its academic discourse.
Fourier was also appointed as the prefect of the Isère département, a period during which his leadership extended beyond the realm of academia. While managing civic responsibilities, he maintained a robust engagement with the scientific community, continually seeking to refine and expand his theories. It is in this capacity, amidst the political shifts and challenges of Napoleonic France, that Fourier demonstrated his versatility both as an administrator and as a scientist.
Advancements in Mathematical Analysis
The theoretical groundwork Fourier laid was not confined to heat equations alone. His mathematical frameworks have been pivotal in advancing broader fields of analysis. The methods he developed to handle differential equations led to techniques still used in complex problem-solving today. His exploration paved the way for further abstractions in mathematics, influencing the likes of Dirichlet and expanding the boundaries of what could be analytically dissected and understood.
One of his major strengths was his ability to utilize and expand the existing mathematical toolbox to deal with problems previously thought to be intractable. He worked on the principles of what we now call Fourier Transform—a tool that enables computation from time domain to frequency domain and vice versa. This approach allows for more profound data interpretation and analysis, making strides in areas such as engineering, natural science, and finance, impacting sectors that Fourier himself might have never envisioned.
Fourier Transform and its Applications
The Fourier Transform is an extension of Fourier's initial work with series and integrates a complex plane to comprehensively interpret various signals. It has become essential for breaking down patterns in large datasets, a task incredibly relevant in today's data-driven world. For instance, in acoustics, this methodology enables the detailed analysis of musical compositions and sound engineering, ensuring high fidelity and nuanced sound reproduction.
In the realm of electrical engineering, Fourier's methodologies are pivotal in the design and functioning of circuits, signal processing, and communication systems. The capability to transform complex signals into simpler forms empowers engineers to design filters and networks with high precision, yielding the robust infrastructure necessary for modern communications.
Moreover, financial sectors extensively use Fourier analysis to model economic trends and forecast market behaviors. In these fields, the ability to predict periodic fluctuations and analyze waveforms of considerable variability is invaluable, equipping analysts with refined tools to predict and hence mitigate market risk.
Fourier's Influence on Modern Physics
Interestingly, Fourier's mathematical legacy also holds critical importance in physics, particularly in understanding wave phenomena and quantum mechanics. His work allows for the deconstruction and study of wave-based behaviors within the quantum realm, offering insights into the wave-particle duality that is central to contemporary physics.
Physicists utilize Fourier analysis to interpret complex waveforms within time-dependent Schrödinger equations, which describe how the quantum state of a physical system changes over time. This application underscores the timeless relevance of Fourier's work and its ability to provide clarity to the abstract and elusive concepts that dominate physics.
Furthermore, the methods established by Fourier have stimulated advancements in optics, specifically in the field of holography and light interference. The study of light wave interactions, diffraction patterns, and optical imaging bears Fourier's intellectual footprints, critical in developing technologies such as laser imaging and fiber-optic communications.
Legacy and Recognition
The magnitude of Jean-Baptiste Joseph Fourier's contributions was recognized during his lifetime, but his impact has only expanded over time. He was elected to the French Academy of Sciences in 1817 and later became a Fellow of the Royal Society in London. Such accolades are a testament to his role as a leader in scientific thought and research.
Fourier's methodologies continue to be applied across myriad disciplines, with researchers and practitioners building upon the robust foundation he established. The applicability of his theories to both theoretical inquiries and practical solutions speaks volumes of their distinct versatility and exceptional depth.
Despite facing challenges during his tenure, including skepticism and resistance from contemporary mathematicians of his day who questioned the rigorousness of his methods, Fourier’s perseverance and groundbreaking findings eventually gained widespread acceptance. Today, his name is not only synonymous with Fourier Series and Fourier Transform, but it also represents a broader paradigm shift in mathematical problem-solving and scientific investigation.
Through his pioneering endeavors, Jean-Baptiste Joseph Fourier transcended the limitations of his era, ushering in analytical approaches that continue to illuminate the complexities of the natural and technological world. In the next part of this article, we will further explore the broader implications of his work and the ongoing research inspired by Fourier's revolutionary theories.
Fourier's Contributions to Engineering and Technology
Jean-Baptiste Joseph Fourier's pioneering insights have extended beyond pure science and mathematics to profoundly influence modern engineering and technology. His mathematical principles underpin many of the structures and systems that form the backbone of contemporary society, illustrating the synergy between scientific inquiry and practical application.
In the realm of civil engineering, Fourier's heat conduction theories have been pivotal in developing more efficient architectural designs, especially in climate control and insulation. His analyses of temperature distribution have enabled engineers to improve energy efficiency in building materials and construction methods, optimizing thermal regulation in residential and industrial settings.
Further, Fourier's analytical techniques have proven indispensable in the design of complex mechanical systems. Military and aerospace engineering notably leverage Fourier analyses for assessing vibration in machinery and aircraft, ensuring structural integrity and performance under variable conditions. In this manner, Fourier's legacy continues to ensure the safety and reliability of critical technological advancements.
Impact on Computational Innovation
In the age of digital innovation, Jean-Baptiste Joseph Fourier's theories hold significant relevance in computational sciences. Fourier's methodologies serve as the groundwork for algorithms used in computational software, which constitute the framework for computer-aided design (CAD), graphics generation, and numerical simulations. By transforming intricate mathematical models into understandable and applicable formats, Fourier's work accelerates computational progress and technological evolution.
Machine learning and data science also benefit from Fourier analysis, particularly in extracting features and patterns from raw data. The ability to transform vast amounts of information into manageable and interpretable segments empowers artificial intelligence systems to perform tasks such as image recognition, voice command responsiveness, and even language processing with enhanced accuracy.
In a more direct sense, Fourier's influence is evident in digital communication systems, where his methods optimize signal clarity and integrity during transmission. Data compression techniques employed in reducing file sizes for quicker and more efficient transmission rely on Fourier's principles to maintain data quality, whether in streaming services or data storage. This foundational role in digital communication underscores Fourier's enduring relevance as society continues to embrace technological progression.
Fourier's Vision and Philosophy
Beyond his scientific exploits, Fourier's philosophical outlook offers insights into his relentless pursuit of knowledge and understanding. Fourier believed deeply in the harmony and interconnectivity of science and mathematics, advocating that they be wielded as complementary forces working towards the betterment of society. His integrative approach underscores the necessity of crossing disciplinary boundaries to foster innovation—a vision increasingly pertinent in today's multidisciplinary research landscapes.
Fourier's work exemplifies the potential inherent in mathematical abstraction to elucidate the concrete, material world. His confidence in the power of mathematical models to solve real-world problems encouraged others to pursue bold and imaginative applications of theoretical frameworks, a vision that continues to inspire generations of scientists, engineers, and thinkers.
The Enduring Legacy of Jean-Baptiste Joseph Fourier
As we conclude our exploration of Jean-Baptiste Joseph Fourier's life and contributions, it is clear that his impact spans across vast realms of science, mathematics, and technology. Fourier's genius lies not only in the elegance and efficacy of his solutions but also in the foresight to recognize and harness the fundamental principles that govern the universe. His work transcends the limitations of time, continuing to guide modern research and innovation.
The influence of Fourier's theories and methods is evidenced by the enduring utilization of Fourier Series and Fourier Transform in academic curricula and professional practice globally. Institutions of higher learning honor his legacy by emphasizing Fourier's analytical approaches in courses related to signal processing, physics, engineering, and applied mathematics.
In technological spheres, Fourier's methodologies remain integral to solving contemporary challenges. As researchers make strides in artificial intelligence, digital communication, and computational modeling, they continue to lean on the robust foundation laid by Fourier's pioneering efforts.
The impact of Jean-Baptiste Joseph Fourier extends into the future, with scientists exploring deeper complexities of the universe, always with the undercurrent of Fourier's vision guiding them. His indelible contributions remind us of the value of curiosity, perseverance, and the relentless quest for knowledge. His work remains a guiding light, illuminating our path forward in an ever-advancing world.
As the scientific community continues to build on Fourier's intellectual legacy, his name endures as a symbol of the boundless potential within the convergence of mathematics and science. This confluence has proven essential for understanding, interpreting, and ultimately advancing the myriad facets of our modern world, a testament to the enduring brilliance of Jean-Baptiste Joseph Fourier.

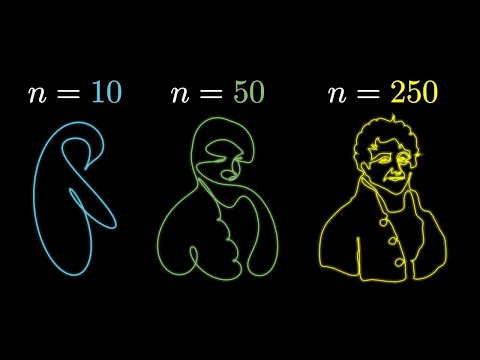



















Comments