Max Born: Pionnier de la physique moderne
Introduction à la vie et au travail scientifique de Max Born
Un génie né sous l'ère d'un révolution scientifique
Né à l'époque des révolutions
Max Karl Ernst Ludwig Born est né le 11 décembre 1882 à Breslau (actuellement Wroclaw), en Prusse-Orientale (aujourd'hui en Pologne), dans une famille savante et cultivée. Ses prétendants maternels comprenaient des universitaires et des scientifiques emblématiques comme Wilhelm Conrad Röntgen, qui remporterait le premier prix Nobel de physique en 1901 pour ses travaux sur les rayons X. Cette atmosphère intellectuelle influença grandement l'orientation scientifique de Born dès son plus jeune âge.
Formation académique et premières expériences scientifiques
Born fit ses études aux Écoles Polytechniques de Breslau et Charlottenburg. C'est là que son intérêt pour la physique expérimentale commença à se développer. En 1903, il obtint un doctorat en physique avec une thèse intitulée “Contribution to the Electrodynamics of Moving Bodies”, une ébauche de ce qui allait devenir son approche mathématique unique et novatrice.
Les théories quantiques et la mécanique des particules
Découvertes cruciales et contributions majeures
Les années 1920 sont considérées comme l'époque dorée de la révolution quantique. Pendant cette période, Born apporta des contributions fondamentales à la compréhension de l'invisible monde qu'il était le premier à décrire avec précision. Il collabora avec Werner Heisenberg et Niels Bohr à Copenhague au Danemark, où leurs efforts conjoints firent émerger la théorie de la mécanique quantique.
En 1926, Born proposa une interprétation des probabilités associées aux ondes de déplacement quantiques décrites par l'equation de Schrödinger. Cette interprétation est aujourd'hui connue sous le nom de principe de Born, qui stipule que l'amplitude complexe de la fonction d'onde au point spatial donné exprime la probabilité d'observabilité d'une partie de la particule au niveau quantique. Cette interprétation était essentielle pour la développement de la mécanique quantique moderne.
L'équation de Born-Green
Au début des années 1930, Born co-implanta aussi l'équation de Born-Green pour le calcul du potentiel électrostatique entre molécules solides, une contribution importante en chimie physicienne. Cette équation continue d'être utilisé en modélisation statistique et en physique des solides.
Enseignement, directions de recherche et reconnaissance internationale
Cours et direction au Technische Hochschule de Stuttgart
En 1921, Born fut nommé pour enseigner au Technische Hochschule de Stuttgart en Allemagne. Là-bas, il continua de développer ses idées sur la physique moderne et à influencer une nouvelle génération de chercheurs. Ses cours étaient appréciés non seulement pour leur profondeur mathématique mais aussi pour sa capacité à connecter la théorie aux aspects pratiques de la science.
Recevant le Nobel de physique
En 1954, Born remporta le prix Nobel de physique en reconnaissance de ses contributions à l’interprétation des fonctions d’onde qui sont au cœur des concepts de la mécanique quantique et en reconnaissance de son approche innovante pour le calcul du comportement de la matière à l’échelle atomique.
Born et la résistance politique en Allemagne
Les années de guerre et l'évasion
Lorsque l'Allemagne nazie estvenue au pouvoir en 1933, Born fut rapidement confronté à des défis politiques. Il refusa de prêter allégeance au parti nazi et préféra partir avec sa famille pour l'Angleterre. Là, il continua son travail scientifique, mais aussi son opposition pacifique à l'idéologie nazie.
Born en Exil à Cambridge et Oxford
A Cambridge, dans le sein de la prestigieuse University Press, Born publiait et enseignait avec la même rigueur académique. Il continua également à écrire sur la philosophie de la physique et l'interprétation des théories quantiques, contribuant ainsi à discuter et à analyser les implications sociétales de son travail scientifique. À la fin de sa carrière, il s'installa à Oxford, où il enseignait et poursuivait ses recherches jusqu'à la fin de sa vie.
Du champ de bataille à la théorie des particules
Dans ces nouveaux lieux, Born continua d'aborder des sujets variés. Son engagement pour le développement des mathématiques appliquées dans la solution de problèmes scientifiques fut particulièrement notoire à la fin de sa vie, lorsqu'il travailla sur un modèle théorique expliquant la structure des atomes et des molécules en termes de nombres entiers.
Cela conclut la première partie de notre article sur Max Born. Il s'agit de l'homme derrière les théories et découvertes qui ont façonné notre compréhension de notre monde quantique. La suite de notre histoire nous guidera dans les détails de ses innovations ultérieures et son héritage en physico-chimie.
Les contributions de Max Born à la physique moderne (suite)
La physique statistique et la structure de la matière
La théorie des particules indéfinies
En plus de son travail sur la mécanique quantique, Born continua d’apporter des contributions significatives aux domaines de la physique statistique et de la structure de la matière. Une de ses plus importantes contributions concerne la théorie des particules indéfinies. Ces travaux, qui portèrent sur la description de systèmes complexes où le nombre de particules peut changer, jouèrent un rôle clé dans la compréhension de la matière à l’échelle atomique et nucléaire. Son approche innovante en matière de théorie des champs statistiques permit d’étendre les principes de la mécanique statistique de Boltzmann et de Gibbs pour expliquer la comportement des système complexes.
La théorie des solides
Born, en collaboration avec le physicien Frederick Lindemann et le chimiste Alfred Landé, contribua de manière significative à la compréhension de la structure des solides. Ensemble, ils développent ce qui est maintenant connu sous le nom de théorie de Born-Lond. Cette théorie, qui explique la structure cristalline des solides en termes de liaisons entre les atomes, a été un pilier fondamental pour la compréhension des propriétés des matériaux.
Le calcul des propriétés des solides
Le modèle de Born-Oppenheimer
L'autre contribution majeure de Born dans la théorie des solides était le modèle de Born-Oppenheimer. Cet modèle, développé en collaboration avec le physicien Hermann Friedrich Arnold, est une approximation fondamentale utilisée en physique des solides pour décrit comment les atomes dans un cristal se comportent sous l'influence des liaisons entre les atomes voisins. Cette approche permet d'identifier les configurations énergétiquement favorables des systèmes de particules, ce qui est crucial pour comprendre les propriétés thermiques, électroniques, et magnétiques des matériaux.
Mesures de rayons X et caractérisation moléculaire
En collaboration avec le physicien Walter Heitler, Born contribua également à la technique des rayons X. Ils travaillèrent ensemble pour améliorer les méthodes de mesure des rayons X et développer des techniques pour la caractérisation moléculaire. Ces travaux ont eu des applications pratiques en chimie et en cristallographie, aidant à décrire la structure tridimensionnelle des molécules et des cristaux.
Le héritage de Max Born
Éducation et transmission des connaissances
En plus de ses travaux scientifiques majeurs, Born s'est engagé dans l'éducation et la transmission des connaissances. Il a écris plusieurs livres de didactique, notamment son célèbre "Principles of Atomic Physics" qui a été largement répandu et utilisé dans les universités. Ses méthodes d'enseignement, basées sur une combinaison de rigueur scientifique et d'accessibilité, ont permis de former une génération de physiciens et de chimistes.
Rôle de mentor et de collaborateur
Max Born a également été un mentor et un collaborateur précieux pour une multitude de jeunes scientifiques. Son approche amicale et son désir d'aider les autres à atteindre leur plein potentiel ont eu des impacts positifs sur la communauté scientifique. Il a supervisé de nombreux doctorats et a participé à des collaborations qui ont abouti à des breakthroughs importants dans la physique moderne.
La vie privée et les intérêts de Max Born
La famille et le temps libre
Born s'est marié deux fois et avait trois enfants de sa première union. Il a toujours gardé une vie relativement simple et modérée, équilibrant sa carrière scientifique avec ses responsabilités familiales. Lorsqu'il n'était pas engagé dans ses travaux de recherche, il aimait profiter du temps libre pour des activités de plein air, comme la randonnée et la plongée sous-marine. Ces intérêts ont souvent nourri sa créativité et sa vision holistique de la science.
La philosophie et l'engagement
Outre ses travaux scientifiques, Born était profondément engagé dans la philosophie de la science et ses implications plus larges. Il publia plusieurs livres et articles sur ces sujets, s'exprimant sur l'interprétation de la théorie quantique et ses implications pour la compréhension de la réalité. Il a également exprimé des critiques constructives au sein de la communauté scientifique, s'engageant à promouvoir des approches éthiques et rigoureuses dans la recherche.
Cela conclut la deuxième partie de notre article consacré à Max Born. Les contributions de Born en physique et en chimie quantique ont réellement façonné notre compréhension moderne du monde à l'échelle atomique. Son héritage est non seulement scientifique mais aussi éthique et philosophique, reflétant la vision de l'homme en tant que scientifique et en tant que citoyen engagé. La suite nous mènera à explorer en profondeur son héritage en physico-chimie et l'évolution des domaines qu'il a ouverts.
Le héritage de Max Born (suite) et l'évolution des domaines qu'il a ouverts
Le héritage et l'impact durable
La continuité de l'héritage
L'œuvre de Max Born a eu une influence durable et significative sur les domaines de la mécanique quantique, de la physique des solides, et de la chimie quantique. Ses principes fondamentaux sur les fonctions d'onde et les probabilités dans la mécanique quantique sont toujours utilisés dans la recherche moderne, et son modèle de Born-Oppenheimer reste un outil essentiel pour la compréhension des propriétés des solides atypiques.
Born et l'enseignement
Max Born fut non seulement un pionnier en recherche, mais aussi un maître éducatif. Ses méthodes pédagogiques et ses livres ont formé une génération de scientifiques. "Principles of Atomic Physics" de Born reste un travail référence pour les étudiants et les chercheurs dans le domaine de la physique des particules. Sa capacité à rendre complexe plus accessible a permis à une large audience de comprendre les principes de la physique moderne.
Étudiants et disciples
Born avait d'innombrables étudiants et collaborateurs qui ont poursuivi des carrières scientifiques prometteuses. Parmi ses collègues, on peut citer les physiciens Werner Heisenberg, J. Robert Oppenheimer, ainsi que le physicien de l'astrophysique, Karl Popper, dont la philosophie de la science a été profondément influencée par les travaux de Born. Cette continuité des générations de scientifiques témoigne de la longévité de son héritage académique et scientifique.
La physico-chimie et l'évolution des domaines qu'il a ouverts
La structure et la dynamique des molécules
La structure et la dynamique des molécules, des cristaux et des systèmes complexes ont évolué en partie grâce aux travaux de Born. Sa contribution à la théorie des rayons X et à la caractérisation moléculaire a transformé la manière dont les scientifiques examinent la structure de la matière. Cette évolution a eu des impacts considérables sur de nombreux champs, notamment la biochimie et la biophysique, avec des applications en sciences de la santé et en technologie biologique.
Applications pratiques et technologies
Les travaux de Born et de ses collaborateurs ont aussi des applications pratiques et technologiques. Par exemple, l'utilisation de la théorie des solides pour comprendre la structure et les propriétés des matériaux a conduit à des avancées dans le domaine de l'électronique et de la nanotechnologie. Les technologies basées sur la structure cristalline des matériaux, comme les semiconducteurs et les matériaux composites, ont profondément transformé l'industrie et la technologie moderne.
La philosophie de la science et l'interprétation des théories quantiques
Born ne s'est pas borné aux sciences purement empiriques. Il a également été un promoteur de la philosophie de la science et de l'interprétation des théories quantiques. Ses écrits et ses discours ont influencé la pensée philosophique sur la nature de la réalité quantique. En soutenant des perspectives élargies sur la science, il a encouragé le dialogue entre la science et la philosophie, contribuant à un équilibre plus large entre les deux domaines.
La legacy de Max Born en conclusion
Un héritage de curiosité et de rigueur
Max Born laissé un héritage de curiosité scientifique et de rigueur intellectuelle. Sa vie et son travail ont été marqués par une constante quête de compréhension et de vérité. Il a montré que la science est à la fois une voie vers la connaissance et un outil pour la résolution des problèmes pratiques du monde qui nous entoure.
Max Born et la science moderne
Max Born est un symbole de la science moderne. Ses contributions ont ouvert des voies inexplorées et ont inspiré des générations de scientifiques. Il a été un mentor, un collaborateur, et un défenseur. Sa vie reflète l'importance de la curiosité scientifique, de la rigueur intellectuelle, et de l'engagement éthique. En tant que scientifique, il s'est consacré à la recherche, mais en tant que citoyen, il a toujours recherché à promouvoir une science plus éthique et plus respectueuse de l'environnement.
Max Born : un héros pour le monde de la science
Max Born est un héros pour le monde de la science. Sa vie est un modèle d'acharnement et d'innovation constante. Il reste un exemple inégalé dans le domaine de la science moderne, et son héritage continue d'inspirer et de guider les scientifiques du monde entier. Sa contribution continue d'influencer la réflexion scientifique et philosophique, offrant des perspectives précieuses sur la nature de la réalité quantique et la place de la science dans le monde.
Max Born a laissé sa marque indélébile sur la science moderne. Sa vie et ses travaux continuent d'être une source d'inspiration pour ceux qui cherchent à comprendre le monde à l'échelle quantique et au-delà. Il nous invite à continuer à explorer, à apprendre, et à innover. En se penchant sur les traces de Max Born, nous continuons de construire un avenir plus scientifiquement éclairé et philosophiquement enrichi.
Max Karl Ernst Ludwig Born, né en 1882 et décédé en 1970, a laissé une empreinte indélébile sur la physique moderne et la science en général. Son héritage est une source d'inspiration et d'enthousiasme, un encouragement constant à poursuivre notre quête de connaissance et de compréhension de la réalité quantique et plus au-delà.


Roger Penrose: Pionnier de la physico-mathématiques et théoricien du temps
L'homme derrière les paradoxes du temps
Roger Penrose, né en 1931 à Colchester dans le Suffolk, est une figure imposante dans le monde des mathématiques et de la physique. Renommé pour ses travaux sur l'espace-temps et l’interaction entre la géométrie et la mécanique quantique, il a contribué de manière décisive à notre compréhension de certaines des concepts les plus complexes et profonds de la science contemporaine. Sa carrière académique fut jalonnée d’importantes réalisations et distinctions, incluant un prix Nobel de Physique en 2020, conféré conjointement avec LIGO scientists pour des découvertes concernant les ondes gravitationnelles.
Un enfance en mouvement
Dès son enfance, Roger Penrose montrait une curiosité et une intelligence hors du commun. Ses parents, Edward et Margaret, lui offrirent une éducation solide dès sa naissance à Colchester. La famille déménagea ensuite vers l'Angleterre du nord où Roger, qui était le fils cadet de six frères et sœurs, se sentit rapidement attiré par la lecture et les sciences. Leur environnement intellectuel fut stimulant – la famille jouissait d’un large éventail de compétences et d’intérêts, influencé par des parents qui étaient tous deux enseignants et passionnés d’arts.
Formation en mathématiques et physique
Penrose a suivi une formation en mathématiques et en physique au King’s College de Cambridge. Il a obtenu sa baccalauréat en mathématiques en 1952. Ayant démontré une aptitude exceptionnelle à résoudre des problèmes complexes, Penrose continua ses études à l'Université de Cambridge et obtint son doctorat en physique théorique en 1957.
L'univers de Roger Penrose
Le travail de Penrose est réparti en plusieurs domaines clés de la science moderne, chacun reflétant une approche multidisciplinaire et créative qui l'a distingué.
Paradoxe de la relativité
L'une de ses contributions les plus marquantes est l’étude des trous noirs. En collaboration avec Stephen Hawking, Penrose prouva que les trous noirs entraînent une singularité dans l’espace-temps dans lesquels les lois de la physique classique ne s’appliquent plus. Une découverte qui a ouvert la voie à l’étude des singularités cosmologiques et gravitationnelles.
Tesselations et pentagones impossibles
Au-delà de la physique, Penrose est également connu pour ses travaux en géométrie purement mathématique. Ses recherches sur les tesselations ont été particulièrement remarquables, notamment ses « pavages non-periodiques » à base du pentagone impossible. Ces formes sont caractérisées par leur capacité inédite à couvrir un plan sans échantillons répétables et continus, une trouvaille qui a eu une influence majeure dans diverses disciplines, y compris l’art et l’architecture.
Impact et reconnitions
Les travaux de Penrose ont reçu une reconnaissance internationale de la part de la communauté scientifique et académique. Il est titulaire de nombreux prix prestigieux, dont le Fields Medal, souvent vu comme le prix Nobel pour les mathématiciens, qu'il a reçu en 1988 pour ses contributions à la théorie des réseaux de particules.
Outre ses contributions scientifiques, Penrose est également connu pour ses écrits populaires en science et sa popularité auprès du grand public, ce qui s'explique par son talent pour vulgariser ses théories complexes. Son livre "The Emperor's New Mind" (1989) est considéré comme un must-read pour ceux qui cherchent à comprendre l'intégration des sciences cognitives au sein de la physique et de la géométrie.
Pas seulement un mathématicien
Roger Penrose va bien au-delà de sa position académique prestigieuse. Il possède une personnalité qui incarne la rigueur scientifique à une époque où les frontières entre les différents domaines de recherche se font de plus en plus floues.
Interdisciplinarité : un mode de pensée à la fois créatif et méthodique
Penrose n'est pas juste un savant qui publie des articles scientifiques complexes. Sa pensée va bien au-delà, combinant l'imagination artistique et la rigueur scientifique. Ce qui est étonnant chez Penrose, c'est sa capacité à mélanger les concepts les plus abstraits de la physique avec ceux de l'art et de l'esthétique. Cette approche interdisciplinaire est exemplaire dans son travail sur les pavements pentagonaux impossibles, une œuvre d'art géométrique unique qui a captivé les artistes, les architectes et les scientifiques.
Collaborations et influences
Penrose a collaboré avec plusieurs figures notables dans le domaine des sciences, mais peut-être l’une des relations les plus influentes est celle avec Stephen Hawking. Ensemble, ils ont publié The Large Scale Structure of Space-Time, un ouvrage de référence dans le domaine qui a révolutionné notre compréhension de l'univers. Outre Hawking, Penrose a également influencé nombre de chercheurs dans ses domaines spécialisés, partageant son savoir auprès de la prochaine génération de scientifiques et encourageant l'échange intellectuel entre différentes disciplines.
Vocations artistique et scientifique
En dépit de l'abstraction de certaines de ses recherches, Penrose ne laisse jamais sa vocation artistique dans l'ombre. Ses dessins et ses travaux sur l’art de impossible sont des témoignages visuels de sa vision mathématique et de son imagination créatrice. Les peintures colorées et les formes complexes des pavages impossibles sont autant de symboles de sa capacité à transcender le monde tangible pour explorer les limites de la géométrie et de l'espace-temps.
Cet aspect artistique de son travail n’est pas négligeable ; il représente une façon de communiquer des concepts scientifiques souvent difficiles à comprendre aux non-initiés. Les illustrations graphiques de Penrose ont non seulement une valeur artistique significative, mais elles sont également des outils puissants de vulgarisation scientifique. Elles permettent ainsi à un public plus large d'accéder aux idées de pointe de la physique et de la géométrie.
La quête de l'infini
Penrose se consacre aussi bien au côté infini de l'univers, à travers les trous noirs et les singularités, que au côté fini de l'esprit humain, en explorant la nature des limitations cognitives de l'être humain face à ces concepts infinis. Cette dualité, caractéristique de sa personne, reflète l’univers qu’il étudie : complexe, à la fois infini et limité.
Culture générale et vulgarisation
Il est particulièrement investi dans la vulgarisation de ses connaissances, en mettant en pratique une forme d'enseignement qui transcende les barrières de la spécialisation en exposant les concepts fondamentaux à un large public. Il a publié de nombreux livres populaires qui démontrent son engagement à rendre la science accessible à ceux qui ne suivraient pas une carrière de chercheur en tant que tel.
Pour Penrose, la vulgarisation n’est pas une simple opération de communication, mais une véritable démarche philosophique et esthétique. En racontant ses découvertes sous un jour accessible et poétique, il aide à maintenir un dialogue fluide entre la science et le grand public.
Conclusion
Roger Penrose est, bien plus qu’un simple mathématicien ou physicien. Sa vie et ses travaux reflètent l’influence indélébile de sa capacité à penser à la fois de manière abstraite et concrète. Chaque aspect de sa vie, de ses collaborations à ses publications en passant par son travail artistique, témoigne d’une approche multidimensionnelle des scientifiques, une combinaison rare de rigueur scientifique et de créativité artistique.
En unissant les concepts les plus abstraits de la géométrie à leurs applications dans le monde physique, Penrose a non seulement avancé nos connaissances scientifiques, mais il a également enrichi notre culture et notre compréhension de l’univers qui nous entoure. Son approche érudite et pédagogique, ainsi que son engagement sans faille dans la diffusion de la connaissance scientifique, lui confèrent une place inégalée parmi les grandes figures de notre époque.
Continuation of Roger Penrose's Scientific Achievements
La gravité dans l'univers et nos perceptions
En plus de ses contributions majeures en physique théorique, Penrose s'est aussi intéressé aux effets de la gravité dans l'univers. Il a mis en lumière les propriétés non intuitives de la gravité, notamment sa capacité à distorcer l'espace-temps et à créer des trous noirs. Son ouvrage The Road to Reality est une encyclopédie en 1000 pages qui décrit l'ensemble des domaines de la physique et des mathématiques, donnant une perspective holistique sur la science moderne, et en particulier sur les théories de la relativité et de la gravité.
La relativité et la théorie quantique
La collaboration avec Stephen Hawking a conduit à de nombreuses découvertes importantes, notamment l'idée que les trous noirs peuvent émettre des radiations, une théorie appelée l'évaporation des trous noirs. Cela a des implications considérables pour la théorie de la gravité et de la théorie quantique. De plus, Penrose a contribué à la compréhension de la singularité en théorie des cordes, un concept qui cherche à fusionner la théorie de la relativité générale avec la théorie quantique.
Autres contributions en mathématiques
Outre la physique, Penrose a également eu un impact considérable en mathématiques. Il a avancé des théories sur la tesselation, qui est la division d'un plan ou d'un espace en des régions non-vide et continus. Son work sur les pentagones tesselants, en particulier les pavages asexués, a été révolutionnaire. Ce concept, où une forme régulière comme un pentagone ne peut être répété de manière périodique sans se chevaucher, a ouvert de nouvelles perspectives en géométrie algorithmique et en art géométrique.
Les applications de la géométrie
La géométrie de Penrose trouve des applications dans de nombreux domaines. Par exemple, les pentagones impossibles sont utilisés en architecture et design, offrant de nouvelles façons d’appréhender l'espace et la forme. Ces formes ont aussi été utilisées en art, influencé par l’œuvre du peintre M.C. Escher, qui lui-même a été fortement inspiré par la géométrie de Penrose.
La géométrie quantique
Penrose a également exploré les liens entre la géométrie classique et la théorie quantique. Il a introduit plusieurs concepts innovants, tels la géométrie non-Euclidienne en dimension supérieure, qui ont des applications potentielles en physique quantique. Ces recherches suggèrent que la géométrie conventionnelle pourrait ne pas suffire pour décrire complètement l'univers à l'échelle quantique, en particulier dans des situations où les effets gravitationnels jouent un rôle crucial.
Le concept de la singularité
Penrose a également exploré les singularités en cosmologie et en théorie des cordes. Une singularité, en physique, est un point où certaines fonctions ou propriétés deviennent infinies ou inconnues. Penrose a montré que certaines des singularités trouvées dans des modèles théoriques peuvent être évitées avec de nouvelles méthodes mathématiques. Il a également introduit le concept de singularité d'horizon cosmologique, un concept qui a d'importantes implications pour la compréhension de l'univers en tant que tout entier.
Les implications de ses recherches
Les recherches de Penrose ont des implications profondes pour notre compréhension de l'univers. Elles suggèrent que la géométrie et la topologie peuvent jouer des rôles plus importants que prévu dans la description de la structure de l'univers. Ces résultats ouvrent de nouvelles voies de recherche dans la fusion de l'astrophysique avec la théorie de la relativité et la théorie quantique, ainsi que des perspectives nouvelles en géométrie et en topologie.
La récente reconnaissance
En 2020, Roger Penrose a reçu le Prix Nobel de Physique, en collaboration avec l'European Gravitational Observatory, pour ses contributions inégalées à la théorie des ondes gravitationnelles. Cela souligne non seulement le prestige de ses travaux, mais aussi leur importance dans les recherches contemporaines en physique. Ces résultats ont ouvert la voie à de nouveaux domaines d'exploration, alliant l'observation directe de phénomènes gravitationnels aux modèles théoriques de la physique.
Diversité des domaines d'étude
En plus des recherches en physique et en mathématiques, Penrose s'intéresse également à d'autres domaines scientifiques. Il a exploré la nature de la conscience, posant des questions profondes sur la relation entre la matière et la conscience. Dans son ouvrage The Emperor's New Mind, il a argumenté que la résolution de certains problèmes computationnels, tels que ceux liés à la réflexion ou la vision, dépendent d'une forme de traitement qui déborde l'algèbre parallèle, suggérant qu'une forme de non-algorithme ou de non-programmabilité est nécessaire. Cette vision a suscité beaucoup de débats, influençant la philosophie et les sciences cognitives.
Engagement avec le public
Comme mentionné précédemment, Penrose est également connu pour son engagement envers la vulgarisation de la science. Il a écrit de nombreux livres accessibles, tels que The Road to Reality et The Emperor's New Mind, qui visent à rendre les découvertes scientifiques plus compréhensibles pour le grand public. Ces écrits non techniques permettent à une gamme large de lecteurs, de ceux qui ont une formation scientifique à ceux qui n'en ont pas, de s'immerger dans les enjeux scientifiques modernes.
Autres contributions en science
Bien que ses contributions soient principalement dans le domaine des mathématiques et de la physique, Penrose a également apporté des contributions notables à d'autres domaines. Par exemple, il a développé des techniques pour analyser des ensembles de données complexes et non-linéaires, ce qui a des applications potentielles dans l'analyse de signaux biologiques et en sciences de l'information. Ces travaux ont aussi une importance significative pour l'analyse de données en médecine et en biologie.
Ces aspects de sa carrière sont une preuve de la polyvalence et de l'approche multidisciplinaire de Roger Penrose. Chaque domaine qu'il aborde, aussi bien en physique, en mathématiques, qu'en science cognitives, est traité avec une rigueur et une créativité qui transcende le cadre strict de la recherche académique.
Engagement et inspiration
En fin de compte, Roger Penrose est un exemple vivant de l'importance de l'innovation et de la persévérance en science. Son engagement et son talent pour mener des projets complexes à travers différentes disciplines continuent d'inspirer des générations de scientifiques et d'intellectuels. Que ce soit à travers sa recherche, sa vulgarisation ou sa participation à des collaborations scientifiques mondiales, Penrose s'est établi comme une figure indiscutable dans le paysage de la science du 21e siècle.
Défis et Futur de la Recherche de Roger Penrose
Les défis scientifiques auxquels Roger Penrose s'est attelé ont été considérables, mais son travail continue d'inspirer de nouvelles questions et de nouvelles avenues de recherche. Les singularités, la gravité et la conscience sont des domaines où de nouvelles découvertes sont attendues. En particulier, la compréhension de la nature précise de la singularité et de l’évation des trous noirs reste un défi majeur pour la théorie de la relativité générale et la théorie quantique.
Défis actuels
Ce qui distingue Roger Penrose, c'est son approche persistante d’exploration de ces questions profondes. Ses recherches sur les singularités, en particulier celles qui se produisent dans les trous noirs et les explosions supernovae, continuent d’ouvrir de nouvelles perspectives en cosmologie et en physique fondamentale. La théorie des cordes et la relativité quantique sont des domaines où ses travaux pourraient encore apporter des progrès significatifs. Chaque nouvelle découverte en physique quantique peut être utilisée pour mieux comprendre ces singularités, et vice versa.
Collaborations et partages d’idées
La collaboration reste une clé pour avancer dans ces domaines. Roger Penrose, en tant qu’une figure de premier plan, a eu beaucoup de discussions et de collaborations avec des scientifiques de renommée. Ces échanges intellectuels ne sont pas seulement académiques ; ils alimentent le processus créatif et scientifique, permettant de nouvelles idées et perspectives. Cela inclut non seulement ses collaborations avec Stephen Hawking, mais aussi avec des chercheurs en géométrie et en théorie quantique.
Futur de la recherche
Le futur de la recherche de Penrose est tout aussi fascinant que ses réalisations passées. Les travaux en théorie des cordes continuent d’attirer beaucoup d’attention, et Penrose a continué de soutenir cette approche en essayant de combiner les concepts de la géométrie et de la théorie quantique. Les découvertes futures en gravité quantique et en cosmologie pourraient résoudre certaines des questions les plus fondamentales sur la structure de l’univers. La géométrie de Penrose pourrait jouer encore un rôle clé dans la compréhension de la nature de la réalité quantique.
Contribution à la culture scientifique
Même au-delà de ses contributions scientifiques, Roger Penrose a marqué la culture scientifique de manières diverses. Il a encouragé l'engagement public en science, inspiré par son engagement envers la vulgarisation. De plus, ses recherches ont influencé la manière dont nous concevons les structures de l'univers et notre compréhension de la conscience. Ses idées peuvent être retrouvées dans des films d'animation, des livres d'art, et même dans la façon dont nous concevons des applications technologiques plus avancées.
Le legacies de Roger Penrose
En fin de compte, Roger Penrose a laissé un héritage indélébile dans la communauté scientifique et culturelle. Ses découvertes continues, sa persévérance et sa capacité à mélanger l'art et la science continuent d'influencer des milliers de personnes à travers le monde. Sa carrière illustre le potentiel de la pensée scientifique quand elle est combinée à la créativité et à l'engagement envers l'éducation et la communication.
En élargissant notre compréhension de l'univers et en influençant des domaines aussi variés que l'art, la technologie, et la philosophie, Roger Penrose a non seulement contribué à une avancée significative dans la science, mais a aussi contribué à enrichir notre compréhension du monde et de notre place dans lui. Chaque découverte, chaque ouvrage, chaque collaboration de Penrose continue d'avancer le front de la science, encourageant un dialogue constant et une quête permanente de la vérité scientifique.
En résumé, Roger Penrose est plus qu'un simple scientifique prolifique ; c'est un catalyseur de la pensée. Son engagement, sa curiosité et sa capacité à transmettre la passion pour la science continuent de faire de lui une figure incontournable dans le panorama de la science contemporaine.
Conclusion
Roger Penrose est une figure incontournable dans le monde de la science. Sa carrière couvre des domaines aussi variés que la physique, les mathématiques, et même l'art, en témoigne sa capacité à lier théorie et pratique, et à transformer les théories abstraites en idées concrètes. Sa quête pour la vérité scientifique et son engagement envers la vulgarisation de la science continuent d'inspirer les chercheurs du monde entier, ainsi que le grand public.
En continuant de pousser les frontières de la science, Penrose nous rappelle que la science est à la fois une démarche individuelle et une communauté. Chaque équation résolue, chaque découverte faite par Penrose est une contribution au patrimoine de la science, et une incitation à continuer de poser les questions qui nous aident à comprendre l'univers qui nous entoure. Son héritage est une source d'inspiration et d'ambition pour les futures générations de scientifiques.
En fin de compte, Roger Penrose est un exemple de ce que peut atteindre une intelligence curieuse et persistante, un esprit créatif et un dévouement à la quête de la vérité. Son travail continue de nous éduquer, de nous inspirer, et de nous encourager à continuer de chercher, d'explorer, et de comprendre le monde qui nous entoure.

Introduction to Quant: A Path to Financial Precision
La quantité, ou quant, représente une branche de l’investissement qui utilise des mathématiques, des statistiques et des modèles informatiques pour prédire les tendances du marché financier. Cette pratique, encore mal connue pour beaucoup, joue un rôle crucial dans la prise de décisions financières à grande échelle. L'objectif de cette article est de décrypter ce que signifie être quant, de mettre en lumière les principes fondamentaux sous-jacents ainsi que les avantages et les défis de cette approche innovante.
La naissance de la quantité: Un tournant pour l'investissement
Avant la révolution digitale, les investisseurs et analystes financier utilisaient des indicateurs et des tendances visibles pour prendre des décisions. Mais avec l’essor de la technologie et l'augmentation des données disponibles, la quantité est devenue une puissante technique pour analyser et anticiper les actions du marché. Cette méthode a vu le jour dans les années 1970, lorsqu'Andrew Lo, un économiste de l'Université de Boston, a introduit le concept de la théorie de marché efficientielle appliquée à des données quantitatives.
Principaux acteurs de la quantité
La réputation de la quantité comme méthode d’investissement s'est renforcée avec l’entrée en scène de grands acteurs tels que Renaissance Technologies, fondée par James Simons, et Two Sigma, dirigée par Nick Colas. Ces entreprises ont démontré l’utilité de modèles mathématiques complexes pour prédire des tendances dans les marchés financiers. En se focalisant sur la prédiction statistique des mouvements du marché, les quantités ont réussi à minimiser les pertes associées aux décisions basées sur le sentiment humain.
Comment fonctionne la quantité: Les principes et les méthodes
La quantité repose sur l’application de principes mathématiques pour analyser des données financières. Les quantitaires utilisent des techniques avancées telles que l’analyse de régression, la théorie des jeux, et la modélisation des risques. Les modèles quantitatifs sont conçus pour prédire le comportement de l'actif ou du marché, ce qui aide les traders et investisseurs à prendre des décisions basées sur des données précises et analytiques, plutôt que sur le jugement subjectif.
Les principaux ensembles de données utilisés
Les quantitaires collectent et analysent de vastes ensembles de données pour identifier des tendances et des modèles. Cela comprend non seulement les données historiques des marchés financiers, mais aussi des indicateurs économiques, des données de marché, des rapports de ventes, et même des tendances sociétales. Ces données sont traitées à l’aide d’algorithmes de machine learning et de traitement du langage naturel pour extraire des insights pertinents.
Les mécanismes de prise de décision en quantité
Une fois analysés, ces ensembles de données sont utilisés pour prédire les comportements futurs des marchés. Les quantitaires utilisent ensuite ces prédictions pour prendre des décisions de trading en temps réel. Ces décisions pourraient porter sur l'achat, la vente ou la vente à découvert d'actifs financiers spécifiques. L'automatisation de ces décisions permet une exécution rapide et efficace, ce qui est essentiel dans des marchés financiers qui évoluent constamment.
Les avantages de l'approche quantitative
La quantité offre plusieurs avantages qui rendent cette approche attractive pour de nombreux investisseurs. Tout d'abord, l'utilisation de techniques quantitatives permet de minimiser la biais humain dans la prise de décision. Le système est conçu pour être objective et basé uniquement sur des données, réduisant ainsi le risque d'erreurs causées par le partialité ou le stress émotionnel.
Efficacité et précision
Deuxièmement, la méthode quantitative offre une exécution efficace et rapide. Les modèles quantitatifs automatisés sont conçus pour réagir immédiatement aux nouvelles données, ce qui peut être crucial lors des fluctuations du marché. Cette rapidité et précision peuvent permettre des gains significatifs pour les investisseurs, en particulier dans les marchés à haut volume et à grande vitesse.
Transparence et dérivation
Enfin, la transparence est une autre atout important. Les méthodes quantitatives utilisées par les quantitaires sont souvent rigoureusement documentées et peuvent être testées et revues par des tiers. Cela contribue à la dérivation, une pratique qui s’assure que les algorithmes sont justes et fiables avant qu’ils soient mis en œuvre en production.
Les défis et les critiques de la quantité
Malgré ses avantages, la quantité n'est pas exempte de défis et de critiques. Une de ses principales critiques concerne l’utilisation abusive des informations. Par exemple, le trading quantitatif massif peut parfois causer des instabilités sur le marché en amplifiant les tendances existantes. Les traders et investisseurs utilisant des outils de trading automatisés peuvent générer des ordres de trading en masse, provoquant une augmentation rapide des prix (ou des baisses) d’un actif.
Impact sur les marchés et la réglementation
Un autre défi est l'impact potentiel sur les marchés financiers. L'automatisation de la prédiction et de la gestion des investissements peut conduire à une sur-saturation de certaines actions et à une pénurie dans d'autres. Cela pourrait créer des conditions économiques défavorables, notamment une réduction des possibilités de gain pour de nombreux investisseurs.
Contestation et scepticisme
Enfin, il y a également des contestations liées à l'utilisation de modèles statistiques complexes. Certains experts et investisseurs soutiennent que les modèles quantitatifs peuvent être simplistes et ne pas tenir compte de certains facteurs clés qui influencent les marchés. Par exemple, la psychologie du marché, les politiques gouvernementales, et les événements imprévus, peuvent avoir un impact significatif sur les investissements et ne pas être tout à fait anticipés par des modèles mathématiques.
Conclusion
La quantité représente une méthode innovante et puissante pour l'investissement, mais elle est évolutive et complexe. Elle offre des avantages tels que la précision, l'efficacité et la transparence, mais elle présente également des défis tels que les risques associés à l'automatisation et la simplification des facteurs de marché. Malgré ces défis, la quantité est une technique en constante évolution, et elle continuera sûrement à jouer un rôle central dans la finance de demain.
La diversification et la gestion du risque en quantité
La diversification est un concept clé dans l'investissement, et la quantité permet de l’appliquer de façon précise et systématique. Les modèles quantitatifs peuvent analyser de nombreuses actions ou actifs et identifier les opportunités de diversification. En combinant divers actifs et en équilibrant leurs performances, les quantitaires peuvent réduire le risque tout en maximisant le rendement potentiel.
Stratégies de diversification en quantité
Il existe plusieurs stratégies de diversification dans le quant. Par exemple, une stratégie de calepinage (pair-trading) cherche à profiter de divergences dans les prix de deux actifs similaires. Lorsque les prix des deux actifs se déparent, une stratégie de calepinage ferait acheter le marché à prix bas et vendre le marché à prix élevé. D'autre part, l'investissement en actions et obligations de divers secteurs peut apporter une stabilité à la portefeuille grâce à une corrélation faible entre les performances des secteurs.
Modèles de gestion du risque
La gestion du risque est également un élément crucial dans la pratique de la quantité. Les quantitaires utilisent des outils statistiques pour estimer et gérer le risque de chaque position dans le portefeuille. Cela permet de prendre des décisions plus prudents et d'équilibrer les retours potentiels avec le risque associé. Par exemple, le portefeuille d’un quant peut comprendre des stratégies de stop-loss pour limiter les pertes sur des positions individuelles, et des techniques de couverture pour protéger contre des fluctuations du marché.
La régulation et le cadre légal en quantité
Comme toute activité financière, la quantité est soumise à un certain éventail de régulations. Les régulateurs tentent de concilier la innovation technologique avec la protection des investisseurs et de la stabilité du système financier. Les principaux enjeux de régulation dans la quantité portent sur l'automatisation de la trading, la divulgation des informations, la transparence des algorithmes, et la gestion des risques associés.
Rôles des régulateurs et des entités de surveillance
L'autorité des marchés des valeurs mobilières (AMF) en France, la Securities and Exchange Commission (SEC) aux États-Unis, et d'autres entités de surveillance financières jouent un rôle clé en mettant en place des régulations pour encadrer la pratique de la quantité. Ces régulateurs établissent des lignes directrices sur la conception et l'utilisation des modèles quantitatifs, l’audit des algorithmes, et la divulgation des informations concernant le trading automatique.
Challenges de la régulation en quantité
La régulation de la quantité pose des défis uniques. Par exemple, l’automatisation du trading peut rendre difficile la supervision en temps réel. Les algorithmes de trading quantitatifs peuvent effectuer des milliers d’transactions par seconde, ce qui rend difficile la mise en œuvre et la supervision d’un contrôle efficace. En conséquence, les régulateurs doivent trouver un équilibre entre l’encouragement de l’innovation et la protection des investisseurs et du système financier.
La formation et les compétences nécessaires pour être quant
En raison de la complexité des techniques utilisées en quantité, une formation spécialisée est nécessaire pour devenir quant. Les candidats potentiels doivent généralement posséder un doctorat en mathématiques appliquées, en statistique, ou en informatique, et avoir de solides connaissances en finance. Cela inclut des compétences en programmation, en mathématiques avancées, et en modélisation financière.
Formation continue en quantité
La technologie et les modèles en quantité sont en constante évolution. Par conséquent, les quantitaires doivent maintenir une formation continue pour rester à jour avec les dernières évolutions dans le domaine. Cela peut passer par des cours en ligne, des ateliers de formation, et des conférences académiques et indus- trielles. Les organisations de trading quantitatif se tournoient pour attirer des talents en établissant des programmes de formation et en offrant des opportunités de recherche et de développement.
Les équipes de trading quantitatif
Les équipes de trading quantitatif sont souvent composées de scientifiques, d'ingénieurs de données, et d'analystes financiers. Chacun d’eux apporte une expertise unique qui contribue à la diversité de la perspective et à la robustesse des modèles. Par exemple, les scientifiques et les ingénieurs de données se chargent de la collecte, de la préparation et de l’analyse des données, tandis que les analystes financiers apportent une compréhension approfondie du marché et des actifs.
Rôles clés dans une équipe de trading quantitatif
Les rôles clés dans une équipe de trading quantitatif comprennent les scientifiques des données, qui sont responsables de la conception et de la mise en œuvre des modèles statistiques et mathématiques. Ils travaillent en étroite collaboration avec les ingénieurs de données qui s’occupent de l'ingestion et du stockage des données. Les analystes financiers jouent également un rôle crucial en fournissant des insights sur les tendances du marché et en aidant à développer des stratégies de trading basées sur ces informations.
Les perspectives futures de la quantité
La quantité est une pratique en constante évolution. Avec l’émergence de nouvelles technologies telles que l'intelligence artificielle et le machine learning, l’avenir du trading quantitatif est prometteur. Ces technologies offrent des possibilités inexplorées pour l’automatisation et l’analyse des données, permettant d'identifier de nouvelles tendances et opportunités de marché.
Intelligence artificielle et apprentissage automatisé
L'IA et l'apprentissage automatique peuvent améliorer la précision des modèles quantitatifs en permettant une analyse plus approfondie et plus rapide de grandes quantités de données. Ces technologies peuvent apprendre à partir des modèles existants et s’adapter aux changes survenant dans le marché, améliorant ainsi la performance des stratégies de trading. En outre, l'IA peut être utilisée pour générer des scénarios de marché futurs, ce qui peut aider les quantitaires à prendre des décisions de trading plus éclairées.
Mise en œuvre de l'intelligence artificielle
La mise en œuvre de l'IA dans la quantité comporte cependant des défis. Par exemple, il est important de veiller à la transparence et à la dérivation, car les modèles d'IA peuvent être difficilement interprétés. De plus, les algorithmes d'IA nécessitent une quantité importante de données pour devenir efficaces, ce qui peut être coûteux et peut poser des problèmes de confidentialité et de protection des données.
Conclusion
La quantité est une approche précise et efficace pour l'investissement, mais elle nécessite une formation et une technologie avancée pour être mise en œuvre de manière efficace. Avec des débats en matière de régulation, une évolution constante en termes de modèles et de technologies, et la présence croissante des équipes de trading quantitatif, la quantité conserve une place centrale dans la finance moderne. En comprenant les enjeux et les défis associés à la quantité, nous pouvons mieux apprécier ses opportunités et ses limites, et décider si cette approche est appropriée pour notre portefeuille financier.
Les défis actuels et les opportunités futures en quantité
Malgré les avancées technologiques et les nombreux avantages, la pratique de la quantité rencontre encore de nombreux défis. Ces défis sont particulièrement pertinents en raison de l'évolution rapide des marchés financiers et des technologies. L'adaptation constante des modèles quantitatifs aux nouvelles données et tendances est cruciale pour rester compétitif.
Les défis actuels en quantité
L'un des principaux défis est la surconsommation de données. Les modèles quantitatifs ont besoin de vastes ensembles de données pour être robustes et précis. Cela peut entraîner des coûts de stockage et de traitement de données considérables, ce qui peut être onéreux pour de nombreuses organisations. De plus, la qualité et l'intégrité des données sont essentielles pour le bon fonctionnement des modèles, et la gestion de ces grandes quantités de données nécessite une technologie avancée et un personnel bien formé.
L'autre défi majeur est la gestion des risques associée à la sur-saturation. Les modèles quantitatifs sont souvent conçus pour exploiter les opportunités de marché, mais ils peuvent aussi créer des sur-saturation dans certains secteurs ou actifs. Par exemple, si de nombreux traders quantitatifs se portent tous sur la même opportunité en même temps, cela peut provoquer des flambées de prix excessives ou une pénurie d'actifs. Cela peut nuire à la stabilité de l'ensemble du marché et créer des risques pour les investisseurs qui sont trop concentrés dans un seul type d'actif ou marché.
Collaboration entre finance et technologie
Un autre défi en cours est la collaboration entre les aspects financiers et technologiques. Les quantitaires doivent non seulement être des experts en finance, mais aussi familiarisés avec les technologies avancées. Cela nécessite une formation croisée et une culture de collaboration entre les équipes financières et les équipes de technologie. Cette collaboration permet de développer des modèles et des stratégies qui explorent pleinement les possibilités offertes par les nouvelles technologies, tout en maintenant des normes élevées de précision et de fiabilité.
Conclusion définitive
La quantité est une approche innovante et puissante qui a révolutionné l'investissement. En offrant des avantages tels que la précision, la précènce, et la diversification, la quantité continue à jouer un rôle important dans la finance moderne. Cependant, elle est également une pratique qui présente des défis uniques, en termes de surconsommation de données, de sur-saturation, et de collaboration interdisciplinaire. Avec une compréhension approfondie des enjeux et des opportunités, les investisseurs peuvent mieux évaluer les avantages et les défis de la quantité et prendre des décisions informées sur son intégration dans leur portefeuille.
En conclusion, la quantité est un domaine en constante évolution qui offre de nombreuses perspectives d'investissement, mais qui nécessite une formation spécialisée et une adaptation constante au marché. En restant attentif aux défis et aux opportunités, les investisseurs peuvent tirer le meilleur parti de cette approche pour maximiser leur rendement et minimiser leur risque.
Joseph Fourier: The Life and Legacy of a Mathematical Trailblazer
Introduction
Joseph Fourier, né Jean-Baptiste-Joseph Fourier, est une figure clé de la science et de l'ingénierie française du 19e siècle. Naissance de l'âge moderne des mathématiques appliquées, Fourier contribue profondément à diversdomaines scientifiques avec ses travaux sur la thermodynamique, l'analyse harmonique, et le traitement des données astronomiques. Cet article explore sa vie et ses contributions scientifiques.
Nouvelle Vie à Paris
Mise en contexte historique, Joseph Fourier est né le 21 mars 1768 à Auxerre en Bourgogne. Après y avoir connu une enfance difficile, il quitte sa ville natale pour Paris où il poursuit ses études à l'École Normale Supérieure. Là-bas, il fait preuve de talent exceptionnel en mathématiques, ce qui lui vaut de nombreux encouragements et le positionne comme un futur prometteur au sein de la communauté académique.
Carrière Académique et Début de la Carrière Publique
Fourier commence sa carrière universitaire comme professeur d'algèbre à l'École Normale Supérieure dès 1794. Cependant, en raison des troubles politiques de la Révolution française qui déstabilisent régulièrement ces institutions, il doit quitter son poste peu après son embauche. En 1795, il obtient un poste de chef de mathématiques au Collège de France, continuant ainsi à enseigner et à s’épanouir dans sa discipline préférée.
Contributions Scientifiques Précoce
Parallèlement à sa carrière académique, Fourier commence à publier ses premiers travaux scientifiques. Ses contributions les plus importantes au début de sa carrière sont dans le domaine de la géométrie descriptive et de la construction de polygones réguliers. Ces travaux témoignent d'un esprit analytique déjà bien développé, qui sera le pilier de ses futurs recherches plus avancées.
Début de Trajectoire Professionnelle
Avec le temps, Fourier est nommé conseiller au Département de la Moselle, une position qui lui permet de s'éloigner de la politique active tout en conservant une influence significative sur la scène nationale. Cette période marque un tournant dans sa vie professionnelle, permettant un équilibre entre ses aspirations académiques et son engagement social.
Travaux Innovateurs sur la Thermodynamique
L'une des plus grandes contributions de Fourier à l'histoire des sciences remonte à 1822 quand il publie sa fameuse thèse sur la propagation de la chaleur dans les corps solides. Ce travail, intitulé "Récherches sur la théorie des corps transparents", présente une analyse mathématique innovante pour décrire le comportement de la chaleur dans différents matériaux. Fourieur défend alors que les températures ne peuvent pas être considérées de manière absolue, mais doivent être mesurées par rapport à l'équilibre thermodynamique. Ces idées novatrices ouvrent la voie à une compréhension plus précise de la thermodynamique et influencent considérablement les recherches futures dans ce domaine.
Astronomie et Analyse Harmonique
Outre la thermodynamique, Fourier fait également des contributions significatives dans l'astronomie et l'analyse harmonique. En particulier, sa méthode des séries de Fourier permet d'exprimer des fonctions périodiques comme une somme infinie de sinus et cosinus. Cette technique innovante a été utilisée ensuite dans une variété de domaines, notamment dans l'ingénierie, la physique, et l'informatique. Ces séries ont également joué un rôle crucial dans le développement de la physique quantique.
Positionnement Académique de Fourier
La carrière de Fourier se développe rapidement avec la réputation croissante de ses travaux. Il est nommé membre correspondant de l’Académie des Sciences en 1807, puis, après quelques années, reçoit un siège permanent au sein de cette prestigieuse institution. Cette reconnaissance lui vaut une plus grande notoriété et lui permet d'engager une recherche plus intensive, notamment dans la résolution de problèmes complexes reliés à la thermodynamique et aux équations différentielles partielles.
Conclusion de la Première Partie
En résumé, la première partie de la vie et des contributions de Joseph Fourier offre un aperçu de son parcours vers la reconnaissance internationale. Ses contributions initiales en géométrie descriptive et en algèbre, suivies de ses travaux innovants en thermodynamique, font de lui une figure essentielle dans l'histoire des mathématiques et de la physique. La publication de sa thèse en 1822, qui marque le début de son impact révolutionnaire, prépare le terrain pour les progrès futurs dans la compréhension de la nature thermique et mécanique des matières, tout en influençant diverses industries et disciplines.
La suite de notre exploration de Joseph Fourier nous attend en seconde partie de cet article, où nous explorerons plus avant ses contributions majeures, sa vie personnelle, et ses relations avec d'autres grands esprits de son époque.
Continuation of Contributions and Impact
Après avoir établi ses fondements théoriques en 1822, Fourier poursuit ses recherches avec une emphase croissante sur l'analyse harmonique et la résolution des problèmes de physique appliquée. Au fil des années, ses travaux continuent à influencer les domaines académiques et pratiques, en particulier dans la thermodynamique et l'électromagnétisme.
Thermodynamique et Égalité Thermodynamique
Les résultats de la théorie de Fourier sur la propagation de la chaleur sont étendus et utilisés pour formuler des principes fondamentaux en thermodynamique, notamment le concept d'équilibre thermodynamique. Ces travaux contribuent à clarifier comment les changements de température se propagent dans une matière, permettant de développer des modèles de conduction de la chaleur utilisés dans des applications allant de l'ingénierie électronique à la météorologie.
Travaux Astronomiques
Apart des contributions en thermodynamique, Fourier a des contributions significatives dans l'astronomie. Sa compréhension de la chaleur et ses méthodes d'analyse ont été appliquées pour expliquer l'origine des phénomènes célestes. Son travail a également contribué à l'établissement de la théorie de l'effet de serre, où il souligne que l'atmosphère terrestre agit comme un isolant thermique grâce à sa capacité à retintre la chaleur provenant du Soleil au lieu de laisser toute cette chaleur s'échapper dans l'espace. Bien que ces idées ne soient pas pleinement reconnues de son vivant, elles préparent le champ pour les futures explorations astrochimiques.
Relations et Influence
Fourier s'est engagé activement dans la rédaction de journaux scientifiques et la publication de ses travaux, ce qui l'a rendu une référence indespensable pour ses contemporains. Il forme plusieurs générations de jeunes chercheurs et ingénieurs, dont certains deviennent eux-mêmes des leaders dans leur domaine. De plus, ses relations avec d'autres savants de l'époque, comme Lazare Carnot et Claude-Louis Navier, ont été importantes pour sa progression scientifique.
Reconnaissance et Décoration
La reconnaissance de Fourier ne se limite pas aux sphères académiques. En 1817, il est nommé inspecteur général de l'enseignement supérieur par Napoléon Bonaparte, un honneur qui souligne sa réputation auprès des dirigeants de l'époque. Bien que Napoléon tombe en disgrâce quelques années plus tard, la reconnaissance accordée à Fourier reflète sa contribution significative à la science française, consolidant sa place dans l'histoire.
Vie Personnelle et Relations Famille
La vie privée de Fourier reste relativement mystérieuse, mais il est mentionné qu'il était marié et avait trois enfants. Bien que sa carrière scientifique soit très bien documentée, son existence personnelle semble moins explorée dans les sources historiques. Il est cependant clair qu'il a réussi à équilibrer sa vie familiale et académique, ce qui témoigne d’une volonté de vivre en accord avec ses valeurs personnelles comme ses engagements professionnels.
Critique et Contestation
Même si ses contributions ont marqué significativement le paysage des sciences, Fourier ne se trouve pas sans contestation. Certains de ses contemporains critiquent ses méthodes mathématiques radicales et contestent certaines de ses conclusions sur la chaleur. Ces critiques, malgré leur pertinence, n'ont pas entravé la popularité croissante de ses idées dans les décennies suivantes.
Décès et Légué
Joseph Fourier est décédé le 16 mai 1830 à Paris, laissant derrière lui non seulement une richesse mathématique et une profonde contribution en physique, mais aussi une留下未完成部分,请继续为您完整剩余内容。
user
continuer le texte svp
Décès et Légué
Joseph Fourier est décédé le 16 mai 1830 à Paris, laissant derrière lui non seulement une richesse mathématique et une profonde contribution en physique, mais aussi une legacy significative qui influence encore de nos jours. Son décès survient quelques semaines seulement après l’éviction de Charles X, une période tumultueuse de l’histoire française. Pourtant, sa mort n’a pas marqué la fin de ses contributions ; au contraire, elle a initié une période de reconnaisance et d’extension de ses théories.
Legacy in Mathematics and Physics
Fort des contributions de Fourier au domaine de l’analyse harmonique, nombre d’études ultérieures s’inspirent et utilisent ses méthodes. La théorie de Fourier joue un rôle crucial dans des domaines aussi variés que l’ingénierie électronique, la physique quantique, et l’informatique. Les séries de Fourier sont utilisées dans la résolution de problèmes complexes en électromagnétisme, en métrologie, et même en analyse des images.
Recognition and Memorials
Après sa mort, Fourier reçoit des honneurs nationaux et internationaux pour sa contribution aux sciences. Il est enterré dans le Père Lachaise cemetery en France, où son tombeau devient un lieu de mémoire pour ses admirateurs et étudiants. Diverses institutions et institutions scientifiques lui sont consacrées, de la ville de Fourier (déclarée station balnéaire en 1884) à des prix et médailles portant son nom.
Cultural Impact and Commemoration
Le nom de Joseph Fourier entre également dans la culture populaire. Il figure dans divers documents d’apprentissage et est souvent introduit aux étudiants comme l’un des pionniers de la physique et de la mathématiques appliquées. Des cours, colloques, et discussions universitaires se dédiennent à ses travaux, renouvelant constamment l’intérêt pour sa pensée scientifique.
Challenges and Future Directions
Tout en reconnaissant les contributions de Fourier, il est important de noter les défis auxquels ses théories ont parfois été confrontées. Les débats philosophiques sur les limites de certaines de ses conclusions continuent encore, notamment en ce qui concerne l’interprétation de phénomènes thermiques complexes. Malgré cela, ses travaux constituent toujours une base indispensable pour la recherche moderne en physique et en mathématiques.
Conclusion
En somme, Joseph Fourier est une figure centrale dans l’histoire des sciences, ayant transformé notre compréhension de la chaleur, de la physique, et de la mathématiques appliquées. Sa vie et ses œuvres sont une source d’inspiration pour les scientifiques et les ingénieurs aujourd'hui, offrant une perspective historique enrichissante sur les développements modernes.
Ainsi, malgré les défis et les critiques, les contributions de Fourier continuent d’inspirer et d’éclairer nos conceptions contemporaines du monde physique. Sa legacy demeure un exemple poignant de l’importance de la persévérance intellectuelle et la passion pour la science.
Note: Pour continuer à faire avancer la recherche sur Fourier, il est essentiel de continuer à explorer sa théorie et à appliquer des méthodes modernes pour mieux comprendre les phénomènes qu'il a mis en évidence. Ces efforts contribueront non seulement à approfondir notre compréhension scientifique, mais aussi à perpétuer le héritage de Fourier.
En conclusion, Joseph Fourier est plus qu’un simple mathématicien ou physicien ; il est une figure éclairante qui a révolutionné les façons dont nous percevons le monde autour de nous.


Enrico Bombieri : Un Génie des Mathématiques Moderne
Introduction
Enrico Bombieri est l’un des mathématiciens les plus brillants et influents du XXe et XXIe siècle. Né en 1940 à Milan, en Italie, il a marqué l’histoire des mathématiques par ses contributions profondes dans des domaines variés, allant de la théorie des nombres à l’analyse complexe, en passant par les équations aux dérivées partielles. Lauréat de la prestigieuse médaille Fields en 1974, Bombieri est reconnu pour sa capacité à résoudre des problèmes parmi les plus ardus de sa discipline. Son parcours, son œuvre et son héritage continuent d’inspirer les chercheurs du monde entier.
Jeunesse et Formation
Un Enfant Précoce
Dès son plus jeune âge, Enrico Bombieri montre des prédispositions exceptionnelles pour les mathématiques. À seulement 15 ans, il est remarqué par des professeurs universitaires pour son intelligence hors du commun. Son talent est tel qu’il est autorisé à suivre des cours avancés à l’Université de Milan alors qu’il est encore au lycée. Cette période marque le début d’une carrière scientifique qui sera jalonnée de succès.
Études Universitaires et Premières Recherches
Bombieri obtient son diplôme de l’Université de Milan en 1963 sous la direction du célèbre mathématicien Giovanni Ricci. Ses travaux de thèse portent déjà sur des questions fondamentales en théorie analytique des nombres, un domaine qui deviendra l’un de ses principaux champs d’investigation. Après son doctorat, il bénéficie de bourses qui lui permettent de voyager et de collaborer avec des sommités internationales, consolidant ainsi sa réputation naissante.
Carrière Académique et Contributions Majeures
La Médaille Fields (1974)
Le sommet de la reconnaissance pour Bombieri survient en 1974 lorsqu’il reçoit la médaille Fields, souvent considérée comme le « prix Nobel des mathématiques ». Cette distinction lui est attribuée pour ses travaux révolutionnaires en théorie des nombres, notamment ses contributions à la résolution partielle de l'hypothèse de Riemann pour les fonctions zêta des corps de nombres. Ce résultat, bien que partiel, représentait une avancée majeure dans l’un des problèmes non résolus les plus fameux des mathématiques.
Domaine de Recherche : Théorie des Nombres
Bombieri a consacré une grande partie de sa carrière à la théorie des nombres, un domaine qui étudie les propriétés des nombres entiers et des structures algébriques associées. Parmi ses nombreux apports, on peut citer le théorème de Bombieri-Vinogradov, un résultat fondamental en théorie analytique des nombres qui donne des estimations précises sur la distribution des nombres premiers dans les progressions arithmétiques. Ce théorème reste aujourd’hui un outil essentiel pour les chercheurs en théorie des nombres.
Travaux Sur les Équations aux Dérivées Partielles
Outre ses recherches en théorie des nombres, Bombieri s’est également illustré dans l’étude des équations aux dérivées partielles (EDP). Ses travaux dans ce domaine ont eu des implications importantes pour la physique mathématique et la géométrie différentielle. Notamment, il a contribué à des avancées sur les problèmes de régularité et les solutions minimales, ouvrant de nouvelles perspectives pour l’analyse non linéaire.
L’Institut des Hautes Études Scientifiques et Princeton
Bombieri a marqué son époque non seulement par ses découvertes, mais aussi par son engagement institutionnel. Après avoir enseigné en Italie, il rejoint l’Institut des Hautes Études Scientifiques (IHES) en France, un haut lieu de la recherche mathématique. En 1977, il part aux États-Unis pour intégrer l’Institute for Advanced Study (IAS) de Princeton, où il côtoie des figures comme André Weil et Kurt Gödel. Ce milieu intellectuel stimulant lui permet de poursuivre des recherches ambitieuses et de former une nouvelle génération de mathématiciens.
Un Héritage Durable
L’œuvre d'Enrico Bombieri se distingue par sa profondeur et son influence durable. Ses méthodes et ses théorèmes font désormais partie intégrante du bagage mathématique moderne. Même aujourd’hui, alors qu’il est professeur émérite à Princeton, ses travaux continuent d’être étudiés et appliqués dans des domaines variés. Son parcours, marqué par la curiosité et l’excellence, illustre la puissance de la pensée abstraite et son impact sur la compréhension du monde.
Conclusion de la Première Partie
La première partie de cet article a retracé les débuts d’Enrico Bombieri, ses contributions majeures en théorie des nombres et son influence sur la communauté mathématique. Dans la suite, nous explorerons davantage ses travaux sur l’hypothèse de Riemann, ses collaborations avec d’autres grands noms des mathématiques, et son rôle dans le développement de nouvelles méthodes analytiques. Nous aborderons également les distinctions qu’il a reçues en plus de la médaille Fields, ainsi que son impact sur l’enseignement et la recherche contemporaine.
...
Enrico Bombieri : Explorateur de l'Hypothèse de Riemann et Collaborations Majeures
L'Engagement envers l'Hypothèse de Riemann
L’un des problèmes les plus célèbres des mathématiques, l’hypothèse de Riemann, a occupé une place centrale dans les recherches d'Enrico Bombieri. Formulée par Bernhard Riemann en 1859, cette conjecture porte sur les valeurs nontriviales de la fonction zêta, dont les zéros sont supposés avoir une partie réelle égale à 1/2. Bien que toujours non résolue, Bombieri a fait des pas historiques vers sa compréhension. En particulier, ses travaux utilisant le crible à grande échelle ont donné des estimations cruciales sur la distribution des nombres premiers sous des hypothèses liées à cette conjecture.
Le Théorème de Bombieri–Friedlander–Iwaniec
En collaboration avec John Friedlander et Henryk Iwaniec, Bombieri a obtenu un résultat majeur en théorie analytique des nombres : le théorème de Bombieri–Friedlander–Iwaniec. Ce dernier affirme que, sous certaines conditions, les nombres premiers sont bien répartis dans des suites très générales. Ce travail, publié en 1986, a révolutionné l’approche des problèmes combinant théorie des nombres et analyse harmonique. Il reste aujourd’hui une référence incontournable pour les recherches sur les asymptotiques des fonctions arithmétiques.
Contributions en Géométrie Algébrique
Outre ses exploits en théorie des nombres, Bombieri a aussi marqué la géométrie algébrique. Dans les années 1970, il développe, avec plusieurs coauteurs, des techniques basées sur les méthodes de descente infinitésimale, qui permettent d’attaquer des problèmes de géométrie diophantienne. Ces outils sont rapidement devenus essentiels pour l’étude des variétés abéliennes et des courbes elliptiques. Ses résultats ont notamment influencé la preuve du théorème de Fermat par Andrew Wiles, bien des années plus tard.
Prix et Distinctions
Au-Delà de la Médaille Fields
Si la médaille Fields est souvent mise en avant, Bombieri a reçu de nombreuses autres récompenses. En 1976, il est honoré par le prix Feltrinelli, l’une des distinctions scientifiques italiennes les plus prestigieuses. Plus tard, en 2010, il décroche le prix King Faisal pour son travail pionnier en théorie des nombres et en analyse. Ces reconnaissances témoignent de l’étendue et de la profondeur de son influence, qui traverse plusieurs sous-disciplines mathématiques.
Membre des Académies les Plus Prestigieuses
Au fil des ans, Bombieri a été élu membre de plusieurs académies nationales et internationales, dont l’Académie des sciences française, la National Academy of Sciences américaine et l’Accademia dei Lincei italienne. Ces affiliations illustrent l’estime dont jouissent ses travaux à l’échelle mondiale. Elles soulignent aussi son rôle de catalyseur pour les collaborations scientifiques transfrontalières, une caractéristique marquante de sa carrière.
Une Influence Pérenne sur les Mathématiques
Impact sur l'Enseignement et la Recherche
Bombieri n’a pas seulement brillé par ses découvertes ; il a aussi façonné le paysage mathématique via son enseignement. À Princeton, ses séminaires sont légendaires pour leur rigueur et leur capacité à synthétiser des idées complexes. Nombre de ses élèves sont devenus des figures majeures à leur tour, perpétuant ainsi son héritage intellectuel. Ses publications, souvent rédigées avec clarté malgré leur technicité, continuent d’être des ressources pédagogiques fondamentales.
Applications Inattendues
Certains résultats de Bombieri ont trouvé des applications inattendues en dehors des mathématiques pures. Par exemple, ses travaux sur les inégalités de Sobolev ont eu des répercussions en physique théorique et en ingénierie, où elles interviennent dans des problèmes d’optimisation et de modélisation des matériaux. De même, ses avancées en théorie analytique des nombres ont alimenté des algorithmes importants en cryptographie moderne.
Un Homme aux Multiples Passions
Art et Science
Bombieri est un esprit profondément polymathe. En plus de ses recherches, il cultive une passion pour l’art, notamment la peinture et la sculpture. Il a d’ailleurs produit plusieurs œuvres abstraites inspirées par des concepts mathématiques. Cette créativité transdisciplinaire, selon lui, nourrit sa pensée scientifique en offrant de nouvelles perspectives sur des problèmes anciens.
Engagement pour la Diffusion des Mathématiques
Bien que discret médiatiquement, Bombieri a toujours soutenu les initiatives visant à populariser les mathématiques auprès du grand public. Il a participé à des conférences grand public et rédigé des articles accessibles pour des magazines scientifiques. Son discours introductif lors de la cérémonie des Fields en 1974 reste un modèle de pédagogie, mélangeant humour et profondeur pour expliquer des idées sophistiquées.
Conclusion de la Deuxième Partie
Dans cette deuxième partie, nous avons approfondi les contributions d’Enrico Bombieri à l’hypothèse de Riemann, ses collaborations majeures et ses distinctions académiques. Nous avons aussi exploré son influence pédagogique et ses passions extra-mathématiques. Dans la troisième et dernière partie, nous examinerons son rôle dans les développements récents des mathématiques, ainsi que les perspectives ouvertes par ses travaux pour les générations futures.
...
Enrico Bombieri : L'Héritage et les Perspectives Contemporaines
Les Avancées Récentes Inspirées par ses Travaux
Au cours des dernières décennies, les idées d'Enrico Bombieri ont continué à porter leurs fruits dans divers domaines mathématiques. En théorie des nombres, ses méthodes de criblage ont été raffinées et appliquées à des problèmes toujours plus complexes. Notamment, les travaux récents sur les « gaps » entre nombres premiers doivent beaucoup à ses techniques innovantes développées dans les années 1960-1970. Plusieurs jeunes mathématiciens ont prolongé ses approches avec succès, prouvant ainsi la fécondité durable de ses idées.
L'Influence sur la Cryptographie Moderne
De manière peut-être inattendue, les recherches de Bombieri ont trouvé des applications concrètes en cryptographie. Son théorème sur la distribution des nombres premiers dans les progressions arithmétiques a directement influencé le développement d'algorithmes de cryptage asymétrique. Aujourd'hui encore, des protocoles de sécurité informatique s'appuient sur des résultats issus de ses travaux, démontrant comment les mathématiques les plus abstraites peuvent avoir des retombées pratiques significatives.
La Quête Continue de l'Hypothèse de Riemann
Malgré les progrès réalisés grâce aux contributions de Bombieri, l'hypothèse de Riemann résiste toujours. Cette persistance fascine toujours la communauté mathématique. Dans son bureau de Princeton, Bombieri continue d'ailleurs à réfléchir à ce problème, proposant occasionnellement de nouvelles pistes. Son approche unique, combinant intuition géométrique et rigueur analytique, inspire les chercheurs actuels qui tentent de résoudre ce « Graal » des mathématiques.
L'École Mathématique Bombieri
L'un des héritages les plus tangibles de Bombieri réside dans le groupe de chercheurs qu'il a formés. Nombre de ses étudiants ont développé des carrières brillantes, perpétuant sa manière combinatoire d'aborder les problèmes. Cette « école Bombieri » se caractérise par un mélange unique d'audace conceptuelle et de minutie technique. Les symposiums organisés en son honneur réunissent régulièrement plusieurs générations de mathématiciens unies par cette approche commune.
Les Défis du XXIe Siècle
Les Nouvelles Frontières en Théorie Analytique des Nombres
Les questions ouvertes que Bombieri a contribué à formuler continuent de guider la recherche actuelle. En particulier, les liens entre fonctions L et formes automorphes constituent un domaine en plein essor, directement issu de ses travaux précurseurs. Les méthodes qu'il a développées servent désormais de base pour explorer des territoires mathématiques encore inconnus, comme certaines conjectures apparentées à la correspondance de Langlands.
Interactions avec la Physique Théorique
De façon surprenante, certaines techniques élaborées par Bombieri ont trouvé des échos en physique théorique contemporaine. Des chercheurs en théorie des cordes utilisent aujourd'hui des outils issus de sa version du principe du maximum pour résoudre des problèmes de compactification. Ces connexions inattendues entre des domaines a priori éloignés confirment la profondeur et l'universalité de ses contributions.
Bombieri aujourd'hui : Le Sage de Princeton
Un Mentor Toujours Actif
Bien qu'officiellement à la retraite, Bombieri reste une présence active à l'Institute for Advanced Study. Il continue de superviser des chercheurs postdoctoraux et participe régulièrement à des séminaires. Ses interventions, toujours précises et souvent visionnaires, témoignent d'une acuité intellectuelle intacte. Pour beaucoup, il incarne le modèle du savant complet, alliant expertise technique et vision large des mathématiques.
Ses Conseils aux Jeunes Mathématiciens
Lorsqu'on lui demande ce qui compte le plus dans la recherche, Bombieri insiste sur deux points : la patience et la curiosité. « Les meilleures idées viennent souvent lorsqu'on explore sans but précis », dit-il souvent. Cette philosophie de la recherche, opposée à l'approche trop utilitariste contemporaine, inspire de nombreux jeunes talents qui voient en lui un modèle de persévérance et d'amour désintéressé pour la science.
Conclusion : Un Monument des Mathématiques
Le parcours d'Enrico Bombieri résume à lui seul les progrès spectaculaires des mathématiques au XXe siècle. De la Médaille Fields à ses contributions toujours actuelles, son œuvre démontre comment une pensée rigoureuse et imaginative peut repousser les frontières du connu. Alors que plusieurs générations de mathématiciens continuent de bâtir sur ses fondations, Bombieri apparaît comme l'un des rares savants ayant marqué durablement plusieurs domaines de sa discipline.
Plus qu'une collection de théorèmes, son héritage est une certaine manière de faire des mathématiques - où l'élégance le dispute à la puissance, où la spécialisation n'exclut pas l'universalité. Dans un monde où la science devient de plus en plus fragmentée, l'exemple de Bombieri rappelle l'importance des esprits synthétiques capables de relier les idées et d'éclairer de nouvelles voies. Son histoire nous enseigne que les plus grandes avancées naissent souvent de la passion pure pour la connaissance, poursuivie avec constance et humilité.
Alors que de nombreux problèmes qu'il a étudiés restent ouverts, une chose est certaine : l'esprit de Bombieri continuera d'inspirer les mathématiciens pour les décennies à venir, guidant peut-être vers la solution des énigmes qui résistent encore aujourd'hui à la puissance de la raison humaine.
Anthemius de Tralles : L'Architecte Génial de Sainte-Sophie
Introduction
Anthemius de Tralles est l’un des architectes les plus talentueux et innovants de l’Antiquité tardive. Né dans la ville de Tralles, en Asie Mineure (actuelle Turquie), au VIe siècle, il est surtout connu pour sa contribution majeure à la construction de la basilique Sainte-Sophie à Constantinople, aux côtés d'Isidore de Milet. Ce chef-d’œuvre architectural, commandé par l’empereur Justinien Ier, a marqué un tournant dans l’histoire de l’architecture byzantine et reste aujourd’hui un symbole de prouesse technique et esthétique.
Les Origines et la Formation d’Anthemius
Né vers 474 apr. J.-C., Anthemius venait d’une famille distinguée dans le domaine des sciences et de l’ingénierie. Tralles était alors un centre intellectuel important, où se mêlaient les savoirs grecs, romains et orientaux. Son père, Stephanus, était un médecin renommé, et ses frères se sont illustrés dans différents domaines, comme la médecine, le droit ou la rhétorique. Cette éducation pluridisciplinaire a probablement influencé la rigueur scientifique et la créativité d’Anthemius.
Bien que peu de détails sur sa formation initiale nous soient parvenus, les sources historiques suggèrent qu’Anthemius a étudié les mathématiques avancées, la géométrie et la physique, disciplines essentielles pour l’architecture et l’ingénierie de l’époque. Son expertise dans ces domaines lui a permis de repousser les limites des techniques de construction traditionnelles.
Le Contexte Historique de Sainte-Sophie
Au VIe siècle, l’Empire byzantine était à son apogée sous le règne de Justinien Ier, qui nourrissait de grandes ambitions pour Constantinople. La capitale impériale devait incarner la puissance et la gloire de l’Empire, et la reconstruction de Sainte-Sophie était au cœur de ce projet. L’ancienne basilique, érigée sous Constantin le Grand, avait été détruite lors de la révolte de Nika en 532.
Justinien souhaitait un édifice sans précédent, surpassant tous les autres en taille et en splendeur. Pour réaliser cette vision, il fit appel à Anthemius de Tralles et à Isidore de Milet, deux érudits réputés pour leur maîtrise des sciences et de l’architecture. Leur collaboration allait donner naissance à un monument révolutionnaire.
Les Innovations Architecturales de Sainte-Sophie
Le principal défi technologique que devaient relever Anthemius et Isidore était la construction d’un dôme massif, plus grand que tout ce qui avait été réalisé jusque-là. La coupole de Sainte-Sophie, haute de 55 mètres et d’un diamètre de 31 mètres, reposait sur un plan basilical classique mais incorporait des solutions ingénieuses pour supporter son poids.
Parmi les innovations majeures figuraient l’utilisation de pendentifs pour distribuer les forces et la mise en place de contreforts dissimulés. Les architectes ont également employé des matériaux légers, comme des briques spéciales et du mortier à séchage rapide, pour alléger la structure. Les fenêtres percées à la base du dôme créaient une impression de légèreté et jouaient avec la lumière, renforçant l’effet céleste voulu par Justinien.
Les connaissances en géométrie d’Anthemius furent cruciales pour les calculs complexes requis par cet édifice. Ses travaux théoriques sur les sections coniques et les propriétés des courbes ont certainement influencé la conception de la voûte.
Anthemius, Mathématicien et Inventeur
En plus de son génie architectural, Anthemius était un mathématicien accompli. Il a écrit plusieurs traités, dont certains ont été partiellement conservés, comme son ouvrage Sur les Miroirs Ardents. Ce texte décrit des dispositifs optiques utilisant des miroirs paraboliques pour concentrer la lumière du soleil, une technique qui aurait pu être utilisée pour des applications militaires ou symboliques.
Son esprit inventif s’est aussi manifesté dans d’autres domaines, comme la mécanique et l’acoustique. Selon certaines sources, il aurait conçu des automates et des dispositifs ingénieux pour le palais impérial, bien que peu de ces réalisations aient survécu.
La Postérité d’Anthemius et de Sainte-Sophie
Malheureusement, Anthemius ne vit pas l’achèvement complet de Sainte-Sophie, car il mourut avant la fin des travaux, laissant Isidore superviser les dernières étapes. Cependant, son héritage perdure à travers ce monument, qui a inspiré des générations d’architectes, des Byzantins aux Ottomans, et jusqu’à l’architecture moderne.
Sainte-Sophie, classée au patrimoine mondial de l’UNESCO, reste un témoignage éclatant du génie d’Anthemius et de son audace technique. Sa capacité à fusionner art, science et spiritualité dans un édifice d’une telle envergure en fait une figure majeure de l’histoire de l’architecture.
Les Défis Techniques Rencontrés par Anthemius
La construction de Sainte-Sophie ne fut pas sans difficultés. Anthemius et Isidore durent résoudre plusieurs problèmes majeurs, notamment liés à la stabilité du dôme. Les tremblements de terre fréquents dans la région de Constantinople représentaient une menace constante pour les structures ambitieuses. Pour y faire face, les architectes imaginèrent des solutions innovantes.
Ils conçurent un système de renforts cachés en pierre et en brique, disposés de manière à absorber les secousses sismiques. Cette technique anticipait en quelque sorte les principes modernes de parasismique. De plus, le choix des matériaux fut judicieux : un mélange de briques légères et de mortier spécial permit de réduire le poids total de l'édifice sans compromettre sa solidité.
La Rupture avec les Traditions Architecturales
Anthemius opéra une véritable révolution en abandonnant certains canons de l'architecture romaine traditionnelle. Alors que les basiliques classiques reposaient sur des colonnades et des plafonds plats, il osa fusionner le plan basilical avec un dôme central massif - une combinaison sans précédent. Cette audace créative permit de concilier la nécessité d'un vaste espace intérieur avec le désir de monumentalité.
L'ingéniosité des pendentifs, ces triangles courbes permettant de faire reposer un dôme circulaire sur une base carrée, marqua un tournant dans l'histoire de l'architecture. Cette solution technique, perfectionnée par Anthemius, influencera toutes les constructions à dôme ultérieures, des églises byzantines aux mosquées ottomanes.
L'Apport Scientifique d'Anthemius
Les travaux théoriques d'Anthemius s'étendaient bien au-delà du domaine architectural. Son traité sur les miroirs ardents révèle une compréhension approfondie de l'optique géométrique. Selon les témoignages historiques, il aurait conçu un système permettant, grâce à des miroirs paraboliques judicieusement disposés, de projeter la lumière solaire sur des cibles précises.
Certains historiens suggèrent qu'il expérimenta avec ces dispositifs pour créer des effets spectaculaires lors des cérémonies impériales. La légende veut même qu'il ait pu mettre au point un système de signalisation optique à longue distance, préfigurant en quelque sorte les communications modernes.
Les Automates et Machines Ingénieuses
Les sources byzantines mentionnent qu'Anthemius conçut divers mécanismes étonnants pour le palais impérial. Parmi ceux-ci figuraient probablement des horloges hydrauliques, des orgues à eau et peut-être même des statues animées. Malheureusement, aucune de ces créations n'a survécu, mais elles témoignent de l'esprit inventif qui caractérisait l'ingénieur de Tralles.
Ces réalisations s'inscrivaient dans la tradition alexandrine des machines merveilleuses, combinant art, science et spectacle. Elles démontrent qu'Anthemius ne se cantonnait pas à l'architecture pure, mais voyait son métier comme une synthèse de toutes les disciplines techniques de son époque.
La Collaboration avec Isidore de Milet
Le partenariat entre Anthemius et Isidore fut crucial pour le succès de Sainte-Sophie. Si Anthemius apportait son génie mathématique et ses innovations structurelles, Isidore complétait ces compétences par sa profonde connaissance des matériaux et des techniques de construction. Les sources anciennes suggèrent que les deux hommes se répartirent les tâches selon leurs spécialités respectives.
Alors qu'Anthemius se concentrait sur les calculs et les plans théoriques, Isidore supervisait davantage les aspects pratiques du chantier. Cette collaboration montre comment, dès le VIe siècle, les grands projets architecturaux nécessitaient déjà une approche pluridisciplinaire et une répartition claire des rôles.
Les Successeurs et la Transmission du Savoir
Après la mort prématurée d'Anthemius, son élève Isidore le Jeune (neveu d'Isidore de Milet) prit le relais pour achever certains détails de Sainte-Sophie. Il est intéressant de constater comment le savoir technique se transmit ainsi à travers des réseaux d'apprentissage formels et familiaux.
Les méthodes calculatoires développées par Anthemius constituèrent pendant des siècles la référence pour les architectes byzantins. On en retrouve des échos dans les églises construites bien après sa mort, jusqu'à la chute de Constantinople en 1453.
L'Influence sur l'Architecture Ultérieure
L'impact de l'œuvre d'Anthemius ne se limita pas à l'Empire byzantin. Lorsque les Ottomans conquirent Constantinople, ils adoptèrent et adaptèrent les solutions techniques de Sainte-Sophie pour leurs propres mosquées. Le célèbre architecte Sinan, au XVIe siècle, reprit et perfectionna nombre des principes établis par Anthemius près de mille ans plus tôt.
En Occident également, pendant la Renaissance, l'étude des écrits byzantins (où la trace des travaux d'Anthemius subsistait) inspira des architectes comme Brunelleschi pour la construction du dôme de Florence. Ainsi, bien que peu connu du grand public, Anthemius peut être considéré comme l'un des pères de l'architecture à dôme dans le monde entier.
La Place d'Anthemius dans l'Histoire des Sciences
Si Anthemius est principalement célèbre pour son œuvre architecturale, ses contributions aux sciences mathématiques et physiques méritent tout autant notre attention. Ses écrits sur la géométrie des coniques, bien que partiellement perdus, représentent une avancée significative par rapport aux connaissances héritées d'Archimède et d'Apollonios de Perga. Les spécialistes modernes reconnaissent en lui l'un des derniers grands géomètres de l'Antiquité tardive.
Ses travaux théoriques sur les miroirs ardents (catoptrique) démontrent une compréhension approfondie des propriétés focales des paraboloïdes. Certains passages suggèrent qu'il aurait pu concevoir des systèmes de signalisation lumineuse ou des dispositifs pyrotechniques, ouvrant des perspectives qui ne seront pleinement exploitées qu'à la Renaissance.
Entre Tradition et Innovation Scientifique
Anthemius illustre parfaitement cette période charnière où le savoir antique, soigneusement conservé à Byzance, commençait à évoluer vers de nouvelles applications pratiques. Contrairement à une idée reçue, le VIe siècle byzantin ne fut pas simplement une époque de conservation des connaissances, mais bien de réelles innovations techniques - dont il fut l'un des principaux acteurs.
Son approche se caractérisait par la synthèse entre la rigueur mathématique grecque et les préoccupations pratiques romaines. Comme en témoignent ses solutions architecturales, il savait adapter ses connaissances théoriques aux contraintes matérielles et aux limites technologiques de son temps.
La Vie Personnelle et le Contexte Culturel
Les sources historiques nous ont malheureusement peu transmis sur la vie privée d'Anthemius. Nous savons qu'il venait d'une famille aisée de Tralles, cité célèbre pour ses écoles de médecine et de philosophie. Son éducation pluridisciplinaire reflète l'idéal encyclopédique caractéristique de l'élite byzantine du VIe siècle.
Les correspondances de l'époque laissent entendre qu'il entretenait des relations étroites avec le cercle intellectuel de Constantinople, comprenant des philosophores néoplatoniciens, des médecins et des juristes. Ce milieu stimulant contribua sans doute à élargir ses horizons bien au-delà des seules techniques architecturales.
La Reconnaissance de Son Vivant
Contrairement à beaucoup d'architectes antiques, Anthemius jouit d'une importante reconnaissance de son vivant. L'empereur Justinien lui accorda des privilèges exceptionnels et le traitement réservé aux plus hauts dignitaires. Ce statut unique pour un "technicien" révèle l'importance accordée à son génie créatif dans le projet politique et culturel de Justinien.
Les chroniqueurs contemporains, comme Procope de Césarée, ne tarissent pas d'éloges sur ses capacités, allant jusqu'à le comparer à Dédale, le mythique architecte du labyrinthe crétois. Cette glorification témoigne du prestige nouveau acquis par les sciences et techniques dans la société byzantine de cette période.
La Disparition d'Anthemius et ses Derniers Projets
Anthemius mourut vers 534, avant l'achèvement complet de Sainte-Sophie (consacrée en 537). Les causes exactes de sa mort restent inconnues, mais certains historiens suggèrent que les tensions et l'immense effort intellectuel requis par le chantier auraient pu altérer sa santé. Une légende rapporte qu'il aurait été foudroyé alors qu'il inspectait les travaux, punition divine pour son orgueil démesuré - récit probablement inventé par des détracteurs jaloux de son génie.
Parmi ses projets inachevés figurait peut-être un traité complet d'architecture et une série d'innovations urbanistiques pour Constantinople. Certaines sources mentionnent des plans pour un nouveau système d'adduction d'eau et des propositions de fortifications avancées, malheureusement jamais réalisées.
La Transmission Fragmentaire de Son Œuvre
L'essentiel des écrits théoriques d'Anthemius a disparu lors des tumultes de l'histoire byzantine. Seuls quelques fragments nous sont parvenus, principalement conservés dans des manuscrits du Xe siècle et des citations chez les érudits arabes. Cette perte considérable prive la postérité d'une partie cruciale de sa pensée créatrice.
Les architectes byzantins ultérieurs, comme ceux qui reconstruisirent le dôme de Sainte-Sophie après son effondrement partiel en 558, semblent avoir eu accès à certains de ses calculs et méthodes, mais sous une forme probablement incomplète et déformée par la transmission orale.
Anthemius dans la Mémoire Collective
Curieusement, malgré l'immortalité de son chef-d'œuvre, la figure même d'Anthemius s'est estompée dans la mémoire collective. Alors que Sainte-Sophie reste un symbole universel, son créateur principal n'est souvent qu'une note en bas de page dans les livres d'histoire. Cette contradiction s'explique en partie par la mentalité médiévale qui tendait à attribuer les grandes réalisations avant tout aux commanditaires (ici Justinien) plutôt qu'aux artisans et techniciens.
Le renouveau des études sur l'Antiquité tardive a cependant redonné à Anthemius la place qui lui revient : celle d'un génie multidisciplinaire à la croisée des mondes classique et médiéval, dont l'œuvre marqua durablement l'histoire de l'architecture et des sciences appliquées.
L'Héritage Contemporain
Aujourd'hui, les architectes et ingénieurs redécouvrent avec intérêt les solutions structurelles imaginées par Anthemius. Ses recherches sur les formes géométriques optimales pour répartir les charges préfigurent les travaux modernes sur les structures légères et les formes actives. Les spécialistes de la restauration des monuments étudient avec attention les techniques qu'il mit en œuvre pour faire face aux défis sismiques.
Plusieurs universités techniques en Turquie et en Grèce ont donné son nom à des départements d'architecture, réhabilitant ainsi la mémoire de ce pionnier méconnu. À Tralles (l'actuelle Aydın), un modeste monument rappelle aux visiteurs que cette ville donna naissance à l'un des plus grands cerveaux techniques de l'humanité.
Conclusion : Le Génie Intemporel d'Anthemius
À travers les siècles, l'œuvre d'Anthemius de Tralles continue d'émerveiller par son audace et sa perfection technique. Plus qu'un simple bâtisseur, il fut un visionnaire qui réussit à synthétiser tout le savoir de son époque pour repousser les limites du possible. Sainte-Sophie demeure aujourd'hui encore un témoignage vivant de ce moment unique où science, art et spiritualité convergèrent vers une réalisation parfaite.
Dans un monde contemporain souvent marqué par la dissociation entre disciplines, la figure d'Anthemius nous rappelle l'importance de l'approche globale, où mathématiques, physique, esthétique et pragmatisme s'unissent pour créer des œuvres qui défient le temps. Son héritage, tant matériel qu'intellectuel, mérite assurément d'être mieux connu et célébré comme l'une des plus belles expressions du génie humain.
Alan Turing : Le Génie Qui a Changé le Cours de l'Histoire
Introduction
Alan Turing est sans conteste l’un des esprits les plus brillants du XXe siècle. Mathématicien, cryptologue, pionnier de l’informatique et philosophe, ses contributions ont non seulement influencé le déroulement de la Seconde Guerre mondiale, mais ont aussi jeté les bases de l’ère numérique dans laquelle nous vivons aujourd’hui. Pourtant, malgré son immense héritage, sa vie a été marquée par des luttes personnelles et une fin tragique. Retour sur le parcours extraordinaire d’un homme dont les idées continuent de façonner notre monde.
Les Années de Formation
Alan Mathison Turing est né le 23 juin 1912 à Londres, en Angleterre. Dès son plus jeune âge, il montre des signes d’une intelligence exceptionnelle. À l’école, il excelle en sciences et en mathématiques, mais ses professeurs remarquent aussi son caractère solitaire et son manque d’intérêt pour les matières traditionnelles. Passionné par les énigmes et les problèmes complexes, Turing trouve refuge dans la logique et l’abstraction.
En 1931, il intègre le King’s College de Cambridge, où il étudie les mathématiques. C’est là qu’il commence à se distinguer par ses idées révolutionnaires. En 1936, il publie un article fondateur, « On Computable Numbers », où il introduit le concept de machine universelle, aujourd’hui appelée « machine de Turing ». Ce modèle théorique est considéré comme la pierre angulaire de l’informatique moderne. Il démontre comment une machine peut effectuer n’importe quel calcul mathématique pourvu qu’il soit exprimé sous forme d’algorithme.
Le Rôle Décisif Pendant la Seconde Guerre Mondiale
Lorsque la Seconde Guerre mondiale éclate en 1939, Turing rejoint Bletchley Park, le centre secret de décryptage britannique. Sa mission : briser le code Enigma utilisé par les forces allemandes pour sécuriser leurs communications militaires. Les messages cryptés par Enigma étaient réputés inviolables en raison de leur complexité. Pourtant, Turing et son équipe relèvent le défi avec brio.
Il conçoit la « Bombe », une machine électromécanique capable de tester rapidement des milliers de combinaisons pour déchiffrer les messages ennemis. Grâce à ses travaux, les Alliés peuvent anticiper les mouvements de l’armée allemande, ce qui joue un rôle crucial dans des batailles clés comme celle de l’Atlantique. On estime que les efforts de Turing et de ses collègues ont permis de raccourcir la guerre de deux ans, sauvant ainsi des millions de vies.
Les Fondations de l'Informatique Moderne
Après la guerre, Turing se tourne vers l’avenir et pose les bases de l’informatique théorique. En 1945, il rejoint le National Physical Laboratory (NPL) où il participe à la conception de l’ACE (Automatic Computing Engine), l’un des premiers ordinateurs électroniques. Bien que le projet ne soit pas mené à terme selon ses plans originaux, ses idées inspirent le développement des ordinateurs modernes.
En 1950, il publie un autre article majeur, « Computing Machinery and Intelligence », où il explore la question de l’intelligence artificielle. Il y propose ce qui deviendra le « test de Turing », un critère pour déterminer si une machine peut être considérée comme consciente. Bien que controversé à l’époque, ce test reste une référence dans les débats sur l’IA aujourd’hui.
Une Fin de Vie Tragique
Malgré ses contributions extraordinaires, la vie personnelle de Turing est marquée par l’adversité. En 1952, il est condamné pour « indécence manifeste » en raison de son homosexualité, alors illégale au Royaume-Uni. Pour éviter la prison, il accepte une castration chimique aux hormones. Humilié et fragilisé, il se suicide le 7 juin 1954 en croquant une pomme empoisonnée au cyanure.
Ce n’est qu’en 2013 que le gouvernement britannique lui accorde une grâce royale posthume, reconnaissant enfin l’injustice dont il a été victime. Aujourd’hui, Alan Turing est célébré comme un héros national et un symbole de la lutte pour les droits LGBT+.
Conclusion Provisoire
La première partie de cet article a retracé les moments clés de la vie d’Alan Turing, depuis ses années de formation jusqu’à ses contributions scientifiques majeures et sa fin tragique. Dans la suite, nous explorerons plus en détail son héritage intellectuel, son influence sur la technologie contemporaine, et les hommages qui lui sont rendus à travers le monde.
>L'héritage intellectuel d'Alan Turing
L'impact des travaux de Turing dépasse largement le cadre de la cryptographie et de la guerre. Ses idées révolutionnaires ont posé les fondations de l'informatique théorique et de l'intelligence artificielle, domaines qui transforment notre société actuelle. Le concept de machine universelle qu'il a développé est à la base de tous les ordinateurs modernes - chaque appareil numérique que nous utilisons aujourd'hui fonctionne selon les principes qu'il a énoncés dans les années 1930.
La machine de Turing et l'informatique moderne
Le modèle théorique de la machine de Turing reste un pilier fondamental de l'informatique. Cette abstraction mathématique simple composée d'un ruban infini, d'une tête de lecture/écriture et d'un ensemble d'états a permis de définir formellement ce qu'est un algorithme. Les informaticiens utilisent encore aujourd'hui ce modèle pour déterminer si un problème peut être résolu par un ordinateur et estimer sa complexité.
Les principes de la machine de Turing se retrouvent dans tous les langages de programmation modernes. Lorsqu'un développeur écrit du code, il crée essentiellement une série d'instructions que l'ordinateur exécute selon la logique établie par Turing. Les compilateurs et interpréteurs qui transforment ce code en instructions machine fonctionnent selon des concepts directement issus de ses travaux.
L'intelligence artificielle et le test de Turing
La contribution de Turing à l'intelligence artificielle est tout aussi fondamentale. Son célèbre test, proposé en 1950, pose une question simple mais profonde : une machine peut-elle penser ? Bien que le test ait été critiqué et remplacé par d'autres approches au fil des décennies, il a lancé le débat sur la nature de l'intelligence et la possibilité de la reproduire artificiellement.
Les systèmes d'IA contemporains comme les réseaux neuronaux profonds et les modèles de langage avancés repoussent constamment les limites de ce que Turing envisageait. Les chatbots capables de conversations naturelles, les systèmes de reconnaissance d'images et les algorithmes de recommandation sophistiqués sont tous des descendants intellectuels de ses idées visionnaires.
L'influence sur la technologie contemporaine
L'impact de Turing sur la technologie moderne est omniprésent mais souvent invisible. Chaque fois que nous utilisons un smartphone, effectuons une recherche sur internet ou interagissons avec un système automatisé, nous bénéficions des avancées rendues possibles par ses travaux.
Cryptographie et sécurité numérique
Les principes cryptographiques que Turing a développés pendant la guerre ont évolué pour devenir la base de la sécurité numérique moderne. Les protocoles qui protègent nos transactions bancaires en ligne, nos communications privées et nos données personnelles s'appuient sur des concepts qu'il a contribué à établir.
Le chiffrement asymétrique, les fonctions de hachage cryptographiques et les systèmes d'authentification modernes doivent beaucoup aux avancées théoriques issues des travaux de Turing et de ses contemporains. Sans ces fondations, l'économie numérique et la cybersécurité telles que nous les connaissons n'existeraient pas.
Algorithmes et traitement de données
L'approche algorithmique que Turing a formalisée est au cœur de la révolution des données. Les systèmes de recommandation, les moteurs de recherche, les outils d'analyse prédictive et les technologies d'apprentissage automatique reposent tous sur la capacité à traiter efficacement de vastes quantités d'information selon des règles logiques.
Les algorithmes de tri, les structures de données et les techniques d'optimisation utilisés quotidiennement par des millions de programmeurs sont des développements directs des concepts introduits par Turing. Son travail a établi les limites théoriques de ce qui peut être calculé et a fourni un cadre pour évaluer l'efficacité des algorithmes.
Les hommages et la reconnaissance posthume
Bien que sa vie ait été écourtée tragiquement, l'importance des contributions de Turing a finalement été largement reconnue. De nombreux hommages lui ont été rendus dans divers domaines, témoignant de l'étendue de son influence.
Reconnaissance académique et scientifique
Le prix Turing, souvent considéré comme le "Nobel de l'informatique", est décerné chaque année par l'Association for Computing Machinery (ACM) à des personnes ayant apporté des contributions majeures au domaine. Créé en 1966, ce prix honore la mémoire de Turing et souligne l'importance durable de son héritage intellectuel.
De nombreuses universités à travers le monde ont créé des chaires, des centres de recherche et des programmes d'études portant son nom. Le Turing Institute au Royaume-Uni, fondé en 2015, est le centre national pour la science des données et l'intelligence artificielle, poursuivant les domaines de recherche qu'il a initiés.
Représentation dans la culture populaire
La vie de Turing a inspiré plusieurs œuvres artistiques et culturelles, contribuant à faire connaître son histoire au grand public. Le film "The Imitation Game" (2014) avec Benedict Cumberbatch dans le rôle principal a particulièrement contribué à populariser son histoire, bien qu'il prenne certaines libertés avec les faits historiques.
Des pièces de théâtre, des romans, des documentaires et même des œuvres musicales ont été créés pour raconter son histoire et explorer son héritage. Ces représentations ont joué un rôle important dans la réhabilitation de sa réputation et la reconnaissance de ses contributions exceptionnelles.
La deuxième partie de cet article a exploré l'héritage intellectuel de Turing, son influence sur la technologie contemporaine et les hommages qui lui sont rendus. Dans la troisième et dernière partie, nous examinerons les questions éthiques soulevées par ses travaux, les développements futurs inspirés par ses idées, et l'importance de préserver son héritage pour les générations futures.
Les questions éthiques soulevées par l'héritage de Turing
L'œuvre de Turing pose des questions éthiques profondes qui résonnent particulièrement à notre époque. D'une part, ses travaux sur l'intelligence artificielle ont ouvert la voie à des développements technologiques transformateurs, mais ils soulèvent aussi des dilemmes moraux cruciaux. D'autre part, sa propre histoire personnelle interroge nos sociétés sur les rapports entre éthique, science et droits humains.
Les défis éthiques de l'intelligence artificielle
Le test de Turing, en proposant d'évaluer l'intelligence des machines par leur capacité à imiter les humains, a involontairement lancé un débat qui dépasse largement le cadre technique. Aujourd'hui, alors que les systèmes d'IA atteignent des niveaux de sophistication impressionnants, nous devons nous interroger : jusqu'où doit aller cette imitation ? Quelles limites éthiques devons-nous établir dans le développement de machines de plus en plus autonomes ?
Les questions que Turing a contribué à poser - sur la conscience artificielle, les droits des systèmes intelligents, et les responsabilités de leurs créateurs - deviennent chaque jour plus pressantes. Les algorithmes qui prennent des décisions affectant des vies humaines (dans les domaines médicaux, judiciaires ou militaires, par exemple) obligent à repenser les cadres éthiques de la technologie.
Science et droits humains : le cas Turing
La persécution dont Turing a été victime en raison de son homosexualité représente un cas emblématique du conflit entre progrès scientifique et régression sociale. Alors que son génie contribuait à sauver des nations et à faire avancer la connaissance humaine, son pays lui refusait le droit fondamental d'être lui-même.
Cette contradiction pose une question cruciale : comment évaluer les sociétés qui, d'une main, célèbrent le progrès technologique, et de l'autre, entretiennent des discriminations ? L'histoire de Turing nous rappelle que le véritable progrès doit être à la fois scientifique et social, technique et humain.
Les développements futurs inspirés par Turing
Les idées de Turing continuent d'inspirer des domaines de recherche à la pointe de la science contemporaine. Plus de soixante-dix ans après ses travaux fondateurs, plusieurs champs prometteurs s'appuient directement sur ses concepts.
L'informatique quantique
La machine de Turing traditionnelle, basée sur des bits classiques, pourrait bientôt être complétée (ou partiellement remplacée) par des ordinateurs quantiques. Pourtant, ces nouvelles machines suivent toujours des principes théoriques compatibles avec le cadre conceptuel établi par Turing. Les chercheurs utilisent aujourd'hui des versions quantiques du modèle de Turing pour explorer les limites du calcul informatique.
De manière fascinante, certains théoriciens suggèrent que les principes de Turing pourraient même s'appliquer à des modèles de calcul encore plus exotiques, comme les ordinateurs biologiques ou neurologiques, élargissant ainsi considérablement la portée de ses idées originelles.
Les neurosciences computationnelles
Les travaux de Turing sur les réseaux neuronaux artificiels ont ouvert la voie à des recherches fascinantes sur le fonctionnement du cerveau humain. Aujourd'hui, les neuroscientifiques utilisent des modèles computationnels inspirés de ses idées pour mieux comprendre la cognition, la mémoire et les processus de décision.
L'approche algorithmique du fonctionnement mental, que Turing fut parmi les premiers à explorer systématiquement, permet maintenant des avancées majeures dans le traitement des maladies neurologiques et la compréhension de la conscience humaine.
Préserver et transmettre l'héritage de Turing
Face à l'importance croissante de l'héritage de Turing, se pose la question cruciale de sa préservation et de sa transmission aux futures générations. Cet effort doit se développer à plusieurs niveaux.
L'enseignement de l'histoire des sciences
Intégrer systématiquement l'histoire des contributions de Turing dans les programmes éducatifs est essentiel. Trop souvent, les étudiants en informatique apprennent les concepts techniques sans comprendre leur origine historique et intellectuelle. Enseigner l'histoire de la machine de Turing, de ses travaux cryptographiques et de ses idées sur l'intelligence artificielle permettrait de mieux situer ces connaissances dans leur contexte humain et philosophique.
Cet enseignement devrait aussi inclure les aspects sociétaux de son histoire, montrant comment les préjugés peuvent coexister avec le progrès scientifique, et comment la société peut parfois rejeter ceux-là mêmes qui la font avancer.
La conservation des archives historiques
Une partie importante des travaux de Turing a été perdue ou détruite, soit pendant la guerre à cause des règles de secret, soit après sa mort. Les documents survivants doivent être préservés avec soin et rendus accessibles aux chercheurs. Le Centre des archives Turing à King's College Cambridge joue un rôle crucial dans cet effort, mais des initiatives complémentaires seraient nécessaires pour reconstituer et numériser l'ensemble de son héritage écrit.
Conclusion : Turing, une lumière toujours vive
Plus de soixante ans après sa mort, Alan Turing reste l'une des figures les plus significatives de la science moderne. Son génie mathématique a transformé notre monde, sa vision a ouvert des horizons que nous explorons encore aujourd'hui, et sa tragédie personnelle nous rappelle les valeurs fondamentales qui doivent accompagner le progrès technique.
À l'ère de l'intelligence artificielle, des big data et de la révolution numérique, nous marchons chaque jour sur les chemins qu'il a tracés. Les défis qu'il a identifiés - comprendre la nature du calcul, définir l'intelligence, concilier technologie et humanité - définissent notre époque autant que la sienne.
Honorer Turing aujourd'hui ne consiste pas seulement à se souvenir de ses prouesses intellectuelles, mais aussi à poursuivre la quête d'une science au service de l'humanité toute entière, sans exclusion ni discrimination. C'est dans cette vision globale, à la fois brillante et profondément humaine, que réside la véritable grandeur de son héritage.



Philolaus : Pionnier de la Pensée Pré-Socratique
Introduction à la Philosophie de Philolaus
La pensée occidentale telle que nous la connaissons aujourd'hui trouve ses racines dans la période antique de la Grèce classique. Parmi les personnalités marquantes de cette époque, certaines restent assez méconnues bien que leur impact sur la philosophie et la science ait été considérable. Philolaus, un penseur pré-socratique crucial, incarne ce phénomène. Né vers 470 avant J.-C. en Italie du Sud, dans la région de la Grande Grèce, Philolaus est souvent associé à l'école pythagoricienne, un groupe de philosophes et de mathématiciens qui vénéraient Pythagore.
Le Contexte Historique et Philosophique
Pour comprendre Philolaus, il est essentiel de replacer sa pensée dans le contexte historique et philosophique de son temps. À l'aube du Ve siècle avant J.-C., le monde grec est en pleine effervescence intellectuelle. Les idées fusent, les théories surgissent, mais surtout, un grand besoin d'expliquer le monde et ses phénomènes surgit. Les pré-socratiques cherchent à comprendre l'univers au-delà des mythes et des traditions, privilégiant l'observation et la raison.
C'est dans cette atmosphère que Philolaus développe ses théories. Élève et peut-être même contemporain de Pythagore, il est profondément influencé par les enseignements de ce dernier, notamment par l'idée de l'harmonie universelle et la centralité des mathématiques. Cependant, il innove en apportant sa propre vision de l'univers.
Les Conceptions Cosmogoniques de Philolaus
Philolaus est principalement connu pour ses théories cosmogoniques originales pour son époque. Contrairement à la vision géocentrique prédominante de son temps, il propose un modèle dans lequel la Terre n'est pas le centre de l'univers. Selon Philolaus, au centre du cosmos se trouve une entité appelée le "Feu central" ou "Hestia". Autour de ce noyau central gravitent non seulement la Terre, mais aussi d'autres corps célestes, dont la Lune, le Soleil et une mythique "Anti-Terre".
Cette perspective révolutionnaire défie non seulement les idées classiques grecques mais préfigure également de nombreux concepts qui seront développés bien plus tard. En utilisant des éléments de la philosophie pythagoricienne, Philolaus propose que les nombres et les rapports mathématiques constituent la structure sous-jacente de l'univers.
L'Influence de la Musique et des Mathématiques
Philolaus et ses contemporains croient fermement que les principes mathématiques sont à la base de toute chose, une idée qui prend racine dans l'harmonie musicale. En effet, le lien entre la musique et les mathématiques est un thème prédominant dans sa pensée. Philolaus, à l'instar des pythagoriciens, insiste sur l'importance des intervalles musicaux et des proportions numériques. Pour lui, l'harmonie universelle reflète l'harmonie musicale, soutenue par des rapports numériques précis.
Cette relation entre musique et cosmologie conduit Philolaus à articuler une conception du cosmos où les corps célestes se déplacent selon des règles harmoniques et mathématiques. Sa théorie, bien que spéculative, ouvre la voie à une vision de l'univers qui intègre sophistication mathématique et contemplation philosophique.
Philolaus, une Porte vers l'Avenir
Si les écrits de Philolaus nous sont parvenus de manière fragmentaire et souvent indirecte à travers les œuvres d'initiés et de commentateurs ultérieurs, son influence reste indéniable. Philosophe précurseur, il introduit des questions et des modèles qui marquent une rupture avec ses prédécesseurs et ouvrent de nouveaux horizons. Sa conception d'un univers organisé autour de principes mathématiques et harmoniques inspire non seulement ses contemporains, mais également les penseurs des générations suivantes.
Philolaus, par sa vision novatrice, place les mathématiques au cœur de la compréhension du monde, préfigurant en quelque sorte les développements scientifiques et philosophiques à venir, œuvre ambitieuse qui mérite un éclairage contemporain approfondi.
Philolaus et l'Évolution de la Pensée Cosmologique
L'impact de Philolaus ne s'arrête pas à ses contemporains immédiats ; il jette également les bases pour l'évolution de la pensée cosmologique à travers les siècles. Son modèle héliocentrique anticipé, bien qu'encore marginal pour son temps, se révèle être une idée avant-gardiste qui influencera plus tard les travaux de penseurs comme Aristarque de Samos et, plusieurs siècles plus tard, Nicolas Copernic. En effet, le concept d'un univers centré non pas sur la Terre mais plutôt autour d'un autre centre renforce une tendance à repenser notre place dans le cosmos.
Bien sûr, il est essentiel de noter que Philolaus ne disposait pas des instruments d'observation ou des avancées scientifiques qui viendront des siècles après lui. Néanmoins, sa capacité à conceptualiser un modèle de l'univers si différent de celui de sa culture témoigne d'un esprit remarquablement ouvert et analytique. Sa pensée invite à réfléchir sur les limites et les potentiels de l'esprit humain en matière de spéculation scientifique.
Contribution à la Métaphysique et à l'Éthique
Les réflexions de Philolaus ne se limitent pas à l'astronomie et aux mathématiques. En tant que membre de l'école pythagoricienne, il est également imprégné de considérations métaphysiques et éthiques. Pour Philolaus, l'univers n'est pas seulement une structure matérielle ; il est également animé par des principes immatériels. Son association avec le pythagorisme signifie qu'il embrasse les idées de réincarnation et de purification de l'âme, aspects fondamentaux de la philosophie pythagoricienne.
En outre, Philolaus adopte la conviction que la connaissance et l'harmonie personnelle proviennent d'une compréhension des lois naturelles. En suivant ces lois, l'individu peut atteindre un état d'équilibre intérieur, reflet de l'équilibre cosmique. C'est dans cette quête d'harmonie que réside une partie de l'éthique pythagoricienne, un ensemble de réflexions sur le mode de vie idéal qui valorise la maîtrise de soi, l'étude et la contemplation.
Philolaus dans les Traditions Philosophiques Postérieures
Les fragments de pensée laissés par Philolaus sont souvent coulés dans la masse des idées pythagoriciennes. Platon, par exemple, est l'un des philosophes postérieurs qui intègre de nombreux éléments pythagoriciens dans sa propre pensée. Bien que Platon ne cite pas explicitement Philolaus, ses idées sur l'harmonie des formes et des nombres résonnent avec les enseignements pythagoriciens que Philolaus aurait contribué à façonner.
D'autres philosophes tels qu'Aristote mentionnent Philolaus directement, bien que souvent de manière critique, en soulignant les aspects plus spéculatifs de ses théories. Malgré cela, ces mentions attestent l'impact durable que ce penseur a eu sur l'héritage philosophique de l'Antiquité. Sa perception d'un univers harmonieux et ordonné par les nombres continue de résonner au sein des horizons philosophiques, mathématiques, et même mystiques.
Un Héritage Persistant
Malgré la perte de nombreuses œuvres originales de Philolaus, son héritage demeure perceptible dans l'évolution de la pensée philosophique occidentale. Les écrits qui nous sont parvenus, bien qu'incomplets, tracent les contours d'un esprit inquisiteur dont les contributions, bien antérieures à celles reconnues de ses contemporains plus célèbres, sont indéniables. En intégrant sa vision du cosmos, de l'éthique et des mathématiques, il insiste sur une dimension intégrative de la connaissance qui invite à repenser les frontières disciplinaires.
De nos jours, la redécouverte de Philolaus révèle non seulement l'histoire d'une tradition intellectuelle mais résonne également avec une démarche actuelle : celle de chercher à comprendre l'univers non seulement par ses manifestations physiques mais aussi par l'harmonie implicite dans ses structures sous-jacentes. Son œuvre, bien qu'ancienne, continue d'incarner un élan vers la compréhension d'un monde où la rationalité et la beauté, l'ordre et la créativité, s'entrelacent.
Philolaus et les Défis de la Transmission des Connaissances
Un défi persistant dans l'étude de Philolaus est la transmission de ses idées à travers l'histoire. Comme pour de nombreux penseurs de l'Antiquité, la préservation de son travail est fragmentaire et souvent filtrée par les interprétations de philosophes ultérieurs. Les sources grecques, telles que celles mentionnées par Aristote et d'autres commentateurs antiques, ont parfois embrouillé les distinctions entre ses idées et celles de la tradition pythagoricienne dans son ensemble.
Cette séparation floue de Philolaus du reste des pythagoriciens nous amène à nous poser des questions sur la nature exacte de sa contribution individuelle. Pourtant, malgré ces incertitudes, les bribes de ses théories ont infiltré la mentalité intellectuelle de son époque jusqu'à des périodes bien plus tardives.
Résonances Modernes de la Pensée de Philolaus
Dans le contexte contemporain, la pensée de Philolaus sur l'harmonie universelle et l'interconnexion par le nombre résonne d'une manière particulière. Avec l'avènement de la physique moderne et de la cosmologie, l'idée de structures universellement organisées rappelle de manière frappante certains de ses concepts archaïques. Par exemple, les travaux sur les constantes cosmologiques et l'harmonie des lois physiques rappellent la fascination de Philolaus pour l'ordre mathématique sous-tendant l'univers.
De plus, dans le champ des humanités numériques et de l'analyse algorithmique, la notion selon laquelle le monde peut être décrit et compris par des modèles mathématiques s'aligne avec la pensée pythagoricienne, contribuant à une nouvelle sensibilité pour l'héritage de Philolaus.
Philolaus, une Source d'Inspiration Transhistorique
Philolaus continue d'inspirer non seulement les philosophes et historiens de la science, mais aussi les artistes et penseurs interdisciplinaires qui cherchent à tisser des liens entre le rationnel et l'artistique, l'ancien et le moderne. Son idée que le cosmos lui-même est une harmonie à explorer plutôt qu'une énigme insoluble motive encore des motifs de recherche et d'expression créative aujourd'hui.
Les écoles de pensée modernes qui explorent la relation symbiotique entre les mathématiques pures et l'esthétique trouvent en Philolaus un ancêtre intellectuel inattendu. Ces écoles prennent appui sur l'idée que les concepts mathématiques ne sont pas seulement des outils de compréhension, mais aussi des miroirs reflétant la beauté inhérente à l'univers.
Conclusion
Il est indéniable que Philolaus, bien qu'il ait vécu il y a plus de deux millénaires, a laissé un marqueur significatif dans le tissu complexe de l'histoire intellectuelle occidentale. Ses contributions, diffuses mais puissantes, continuent de nourrir notre compréhension de l'univers et de notre relation avec lui. À mi-chemin entre science, philosophie et mysticisme, Philolaus se tient comme un phare qui éclaire la voie des explorations scientifiques et métaphysiques qui défient les frontières conventionnelles.
Sa vision représente non seulement une étape importante dans le développement de la pensée philosophique antique, mais elle offre aussi une perspective précieuse sur les questions émergentes qui animent les débats intellectuels contemporains. En honorant son héritage, nous pouvons continuer à explorer les mystères de notre monde avec le même sens de curiosité et d'ouverture d'esprit qui a animé Philolaus et ses successeurs.
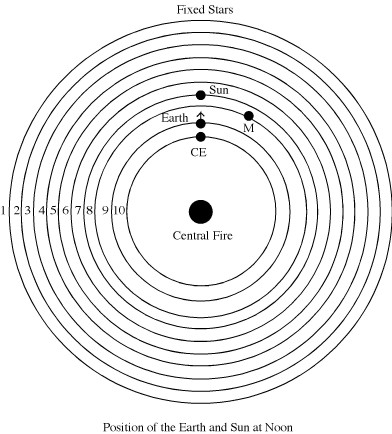

Jean-Pierre Serre : Un Génie des Mathématiques Modernes
Introduction au parcours exceptionnel de Jean-Pierre Serre
Jean-Pierre Serre, une figure emblématique des mathématiques modernes, est souvent cité comme l'un des plus grands mathématiciens du XXe siècle. Né le 15 septembre 1926 à Bages, une petite commune dans le sud de la France, Serre a marqué l'histoire par ses contributions fondatrices dans divers domaines des mathématiques, notamment la topologie, la théorie des nombres et la géométrie algébrique. Ce brillant chercheur, souvent décrit comme un prodige des mathématiques, a vu sa carrière parsemée de distinctions prestigieuses, récompensant l'impact profond de ses travaux sur la communauté mathématique mondiale.
Les débuts prometteurs de Serre
Dès son plus jeune âge, Jean-Pierre Serre manifeste un intérêt particulier pour les mathématiques. Élève brillant, il poursuit ses études à l'École Normale Supérieure de la rue d'Ulm à Paris, où il obtient l'agrégation de mathématiques en 1948. C'est durant cette période qu'il commence à travailler avec Henri Cartan, un autre mathématicien de renom, qui deviendra plus tard une influence cruciale dans sa carrière.
C'est au début des années 1950 que Serre commence véritablement à se faire un nom dans le milieu académique. À seulement 27 ans, en 1954, il reçoit la prestigieuse médaille Fields, souvent appelée le "Prix Nobel des mathématiques", pour ses travaux révolutionnaires en topologie. Cette distinction fait de lui le plus jeune lauréat de l'histoire à cette époque, confirmant son statut de génie précoce.
Contributions fondamentales et interdisciplinaires
Jean-Pierre Serre se distingue non seulement par sa précocité, mais aussi par la diversité et la profondeur de ses recherches. Ses contributions couvrent une vaste étendue de disciplines mathématiques, montrant une capacité exceptionnelle à briser les barrières entre les sous-domaines des mathématiques.
En topologie, il est connu pour ses travaux sur la théorie des faisceaux et les théories homotopiques. Son traitement novateur des structures algébriques a ouvert de nouvelles perspectives et a influencé de nombreux travaux ultérieurs. Par ailleurs, en géométrie algébrique, Serre a joué un rôle clé dans le développement des fibrés vectoriels et dans l'interaction entre algèbre et géométrie, particulièrement à travers ses recherches sur les schémas.
Sa collaboration avec Alexandre Grothendieck, un autre colosse des mathématiques, a été particulièrement fructueuse. Ensemble, ils ont posé les bases d'une révolution en géométrie algébrique moderne. Leurs travaux ont mené à la création de théories et concepts qui sont devenus des outils standards pour plusieurs chercheurs contemporains.
Théorie des nombres et l'influence durable de Serre
Jean-Pierre Serre n'a pas seulement été un pionnier en topologie et en géométrie, mais il a également apporté d'importants progrès à la théorie des nombres. Ses contributions dans ce domaine sont non seulement théoriques mais aussi appliquées, inspirant de nouvelles discussions et recherches.
En travaillant sur la théorie des groupes et les représentations galoisiennes, Serre a introduit le prolongement de nouvelles techniques pour aborder les problèmes classiques de la théorie des nombres. Ses idées sur la modularité et la symétrie ont permis de nouvelles perspectives sur des équations jusqu'alors ardues, influençant notablement les travaux autour du dernier théorème de Fermat, qui a finalement été démontré par Andrew Wiles à l'aide de fondations posées par Serre.
Une carrière récompensée par de prestigieuses distinctions
Face à une carrière aussi prolifique, Jean-Pierre Serre a reçu une multitude de reconnaissances. Outre la médaille Fields, il a été lauréat de nombreux autres prix prestigieux tels que le prix Abel en 2003, le prix Balzan en 1985, et bien d'autres. Chacune de ces distinctions souligne la portée de ses contributions et l'importance de ses découvertes dans le paysage mathématique contemporain.
Serre, tout au long de sa carrière, a également été un membre actif et respecté de l'Académie des Sciences française. Il est surtout reconnu pour la clarté de ses travaux, non seulement par leur complexité technique mais aussi par l'élégance et la concision de ses démonstrations, qui restent un modèle d'inspiration pour les générations futures de mathématiciens.
En conclusion, l'histoire et l'héritage de Jean-Pierre Serre illustrent la manière dont une passion inébranlable pour les mathématiques peut transformer le monde scientifique, inspirant nombres de personnes et ouvrant la voie à des découvertes futures. Sa carrière demeure à la fois un exemple et un sujet d'étude pour ceux qui aspirent à innover dans le domaine des sciences mathématiques.
Une influence pédagogique et intellectuelle majeure
Au-delà de ses contributions purement académiques, Jean-Pierre Serre a également laissé une empreinte durable en tant qu'éducateur et mentor. Professeur au Collège de France de 1956 à 1994, il a formé plusieurs générations de mathématiciens qui ont eux-mêmes marqué le domaine. Sa manière d'enseigner, basée sur la rigueur et l'innovation, a inspiré de nombreux étudiants à poursuivre des carrières en mathématiques pures et appliquées.
Serre a aussi joué un rôle crucial dans la diffusion des idées mathématiques modernes. Il a participé à de nombreux colloques et conférences, partageant ses connaissances et ses découvertes avec la communauté scientifique mondiale. Cette ouverture et cette volonté de transmission sont devenues une sorte de signature, renforçant sa stature non seulement comme chercheur, mais aussi comme éducateur dévoué.
Les ouvrages fondamentaux de Serre
Dans sa démarche de diffusion et de partage, Jean-Pierre Serre a rédigé plusieurs ouvrages qui sont devenus des références indispensables pour les étudiants et les chercheurs. Parmi eux, la publication de "Cours d'arithmétique" et "Algebraic Groups and Class Fields" ont notamment illustré son approche pédagogique unique, combinant simplicité et profondeur.
Ses écrits sont reconnus pour leur clarté et leur précision. Chaque ouvrage de Serre contient non seulement les découvertes mathématiques proprement dites, mais aussi une façon unique de penser et d'aborder les problèmes, ce qui a permis à de nombreux lecteurs de s'approprier et de comprendre des concepts complexes. Cette clarté didactique place ses œuvres parmi les manuels les plus prisés dans le monde de l'enseignement des mathématiques.
Un regard vers l'avenir : Les implications contemporaines des travaux de Serre
Les contributions de Jean-Pierre Serre ne se limitent pas à l'histoire des mathématiques, elles continuent d'offrir des outils et des perspectives cruciales pour les chercheurs actuels. Ses travaux en topologie, en géométrie algébrique et en théorie des nombres ont posé les bases de nombreux développements contemporains.
Aujourd'hui, des concepts introduits par Serre s'appliquent non seulement à des domaines purement théoriques, mais aussi à des champs interconnectés, tels que la physique théorique et l'informatique. Par exemple, ses recherches sur les groupes de Lie et les structures algébriques trouvent des applications en cryptographie moderne, un témoignage de la polyvalence et de la modernité de ses idées.
Les connexions interdisciplinaires qu'il a envisagées et développées sont emblématiques de l'ouverture d'esprit et de la curiosité intellectuelle qui ont toujours marqué sa carrière. Grâce à ces ponts entre les disciplines, Serre a non seulement enrichi les mathématiques, mais a aussi contribué à des avancées technologiques et scientifiques plus larges.
L'héritage d'un visionnaire
L'impact de Jean-Pierre Serre continue de se faire sentir dans les nombreuses manières dont il a influencé les mathématiques et la science en général. Ses collaborateurs et successeurs dans le domaine académique poursuivent et étendent ses travaux, témoignant de l'influence durable de ses contributions. Également, son approche intégrative et sa curiosité intellectuelle restent des piliers pour les jeunes chercheurs qui entrent dans le monde fascinant des mathématiques.
Au-delà de ses succès personnels, l'héritage de Jean-Pierre Serre réside dans l'inspiration qu'il a su insuffler à toute une communauté de mathématiciens passionnés. Les conférences, les symposiums et les groupes de recherche qui portent son influence continuent de prouver que son travail a jeté des bases solides pour des décennies de recherches futures. À chaque génération de chercheurs, Serre offre un modèle de passion et d'excellence, insufflant le désir d'explorer de nouvelles frontières.
Conclusion : Une carrière sans fin
Bien que Jean-Pierre Serre ait pris sa retraite officielle, son influence et ses découvertes résonnent toujours dans les mathématiques contemporaines. Ses contributions ont non seulement enrichi notre compréhension du monde mathématique, mais ont également prévu des possibilités presque infinies pour l'avenir. La carrière de Serre, parsemée de distinctions et de réalisations, continue d'être une source d'inspiration pour les mathématiciens du monde entier, libérant chaque jour de nouvelles potentialités dans ce vaste univers qu'est celui des mathématiques.
Ainsi, Jean-Pierre Serre n'est pas seulement un éminent scientifique d'hier, mais un acteur clé et résolument contemporain des mathématiques modernes. Son héritage continue de prospérer et de transformer le paysage mathématique pour les générations à venir.
Un testament d'humanité et de simplicité
Au-delà de ses immenses contributions académiques, Jean-Pierre Serre est souvent décrit par ses pairs comme un individu d'une grande humanité et simplicité. Malgré son statut légendaire dans la communauté mathématique, il a toujours su rester accessible et ouvert au dialogue avec ses collègues, ses étudiants et même les passionnés de mathématiques intéressés par ses travaux.
Ces qualités transparaissent également dans sa manière de communiquer ses idées. Serre a toujours privilégié une approche fondée sur la clarté, cherchant à rendre ses idées compréhensibles pour un public aussi large que possible. Sa capacité à rendre accessibles des sujets complexes témoigne non seulement de son talent scientifique, mais aussi de son profond respect pour le partage des connaissances.
Les témoignages de ses confrères
Nombreux sont ceux qui ont travaillé aux côtés de Jean-Pierre Serre et qui témoignent de la profonde admiration qu'ils lui portent. Des collègues à l'international, des étudiants devenus à leur tour éminents chercheurs, ainsi que des institutions académiques, célèbrent tous le génie et l'apport de Serre à travers le monde.
Dans les mots de ses contemporains, Serre est souvent décrit comme quelqu'un d'une exceptionnelle intégrité intellectuelle. Il a toujours recherché la vérité mathématique avec humilité et rigueur, ce qui a inspiré des générations entières de mathématiciens. Ces témoignages soulignent également sa capacité unique à encourager et stimuler la créativité et l'innovation chez ceux qui l'entouraient.
Un engagement continu pour l'enseignement et la recherche
Même après sa retraite officielle, Jean-Pierre Serre n'a jamais véritablement quitté le monde des mathématiques. Il a continué de participer activement à des conférences, offrant ses conseils et son expertise à de nombreux projets de recherche. Sa volonté de transmettre ses connaissances et d'encourager les jeunes chercheurs à posser les frontières du savoir ne s'est jamais estompée.
Serre a également participé activement à des initiatives visant à promouvoir les mathématiques auprès du grand public, soulignant l'importance de cette discipline dans notre compréhension du monde et son rôle fondamental dans les avancées technologiques et scientifiques. Par ses activités et son engagement continu, il a contribué à renforcer le lien entre la communauté mathématique et le reste de la société.
Une inspiration pour les générations futures
L'influence de Jean-Pierre Serre dépasse largement les frontières académiques. Son parcours, qui allie une extraordinaire carrière scientifique à des qualités humaines hors du commun, constitue une source d'inspiration pour bien des gens. Tant pour ceux qui se lancent dans les mathématiques que pour ceux qui s'y intéressent en tant qu'amateurs passionnés, l'exemple de Serre illustre ce qu'il est possible d'accomplir grâce à la curiosité intellectuelle et à la persévérance.
Les institutions éducatives continuent de citer son travail et ses méthodes pédagogiques comme modèles de réussite et d'excellence. Son nom est attaché à des bourses et des récompenses qui visent à encourager et soutenir les jeunes talents dans le domaine des mathématiques, propulsant encore plus loin son impact positif sur le monde scientifique.
Conclusion : L'empreinte indélébile de Jean-Pierre Serre
En rétrospective, la vie et la carrière de Jean-Pierre Serre illustrent magnifiquement l'impact que peut avoir un individu dédié à la quête de connaissances. Son parcours est un témoignage vivant de ce qu'une passion inlassable pour les mathématiques peut accomplir, à la fois pour l'avancement de la science et pour l'inspiration de milliers de personnes à travers le monde.
Son héritage ne repose pas seulement dans les théorèmes et les structures qu'il a développés, mais aussi dans les vies qu'il a influencées. Jean-Pierre Serre a montré au monde que les mathématiques ne sont pas seulement une collection d'équations et de théories abstraites, mais une véritable aventure humaine, propulsant la compréhension et la connexion autour de questions fondamentales de l'univers. À travers ses travaux, il nous laisse un cadeau inestimable, celui de l'exploration perpétuelle et du courage d'aller au-delà des limites du possible.


James Clerk Maxwell : Le Père des Théories Électromagnétiques
Introduction à une Figure Pionnière
James Clerk Maxwell est souvent méconnu du grand public, pourtant son influence sur la science moderne est incommensurable. Né le 13 juin 1831 à Édimbourg, en Écosse, Maxwell a compté parmi les esprits les plus brillants du XIXe siècle. Physicien et mathématicien, ses contributions ont jeté les bases de nombreuses technologies contemporaines, du téléphone portable aux transmissions par satellite, grâce à ses explorations dans le domaine de l'électromagnétisme. Avec ses fameuses équations de Maxwell, il a unifié les concepts disparates de l'électricité et du magnétisme en une théorie cohérente qui a révolutionné notre compréhension de la physique.
Les Premières Années
Maxwell a démontré un esprit curieux dès son plus jeune âge. Fils unique d'une famille écossaise bien instruite, il a reçu une éducation exceptionnelle qui a nourri son intérêt pour la science et les mathématiques. À 14 ans, il a intégré la prestigieuse Edinburgh Academy, puis a poursuivi ses études à l'Université d'Édimbourg et au Trinity College à Cambridge. Il a rapidement été reconnu pour ses capacités intellectuelles, publiant son premier article scientifique à seulement 14 ans, sur la géométrie des courbes elliptiques.
La Trilogie Électromagnétique
Lorsque Maxwell a commencé ses travaux sur l'électricité et le magnétisme au milieu du XIXe siècle, ces deux domaines étaient considérés comme des phénomènes indépendants. Les travaux de Michael Faraday sur les lignes de force ont inspiré Maxwell, qui a traduit ces concepts qualitatifs en formules mathématiques rigoureuses. En 1861-1862, il a publié une série d'articles intitulée "On Physical Lines of Force" qui a établi les fondations de la théorie électromagnétique. Cependant, c'est en 1865, avec son article "A Dynamical Theory of the Electromagnetic Field", que ses quatre équations magistrales ont vu le jour.
L’Unification des Forces
Les équations de Maxwell sont un exploit remarquable car elles unifient les phénomènes électriques et magnétiques en un seul champ électromagnétique. Ces quatre équations décrivent comment les champs électriques et magnétiques sont générés par les charges électriques, le courant électrique, et comment ils se propagent dans l'espace. L'unification de l'électromagnétisme a non seulement conduit à la prédiction de l'existence des ondes électromagnétiques, mais a aussi préparé le terrain pour la théorie de la relativité d'Albert Einstein.
Impact sur les Ondes Électromagnétiques
Une des prédictions les plus saisissantes de l'œuvre de Maxwell était que des ondes électromagnétiques devraient exister et se propager à la vitesse de la lumière. Ce qui était avant tout une implication théorique devient réalité grâce à Heinrich Hertz, qui, à la fin des années 1880, a prouvé expérimentalement l'existence des ondes radio. Cette découverte a conduit à l'essor des télécommunications modernes, de la radio à la télévision, en passant par les technologies Wi-Fi et Bluetooth, soulignant l'impact durable des théories de Maxwell.
Un Modèle pour l'Étude de la Lumière
Maxwell a également révolutionné notre compréhension de la lumière. Avant ses travaux, la lumière était généralement considérée comme une onde purement mécanique. En démontrant que la lumière est une forme de rayonnement électromagnétique, il a intégré la science optique à celle de l'électromagnétisme, fournissant des perspectives entièrement nouvelles pour les sciences physiques. Cela a non seulement transformé la photographie et l'optique, mais a aussi inspiré de nouveaux domaines de recherche, tels que la spectroscopie, qui utilisent la lumière pour sonder les propriétés de la matière.
Dans cette première partie de notre exploration de la vie et des œuvres de James Clerk Maxwell, nous avons abordé ses premières contributions et l'impact fondamental de ses théories électromagnétiques. Le voyage continue dans la deuxième partie, où nous plongerons plus profondément dans ses autres contributions scientifiques et son héritage.
La Théorie Cinétique des Gaz
En dehors de ses travaux révolutionnaires sur l'électromagnétisme, Maxwell a considérablement contribué à la physique statistique, notamment à travers la théorie cinétique des gaz. Cette théorie, développée dans les années 1860, explique les propriétés thermodynamiques des gaz en termes de mouvements moléculaires. En collaborant avec Ludwig Boltzmann, Maxwell a introduit la distribution de Maxwell-Boltzmann, une formule statistique qui décrit la distribution des vitesses des molécules dans un gaz à température donnée.
Ce travail a transformé notre compréhension de la thermodynamique et a permis de relier les notions de température et de chaleur à l'énergie cinétique des particules. Avant Maxwell, les propriétés des gaz étaient abordées principalement de façon empirique. En décrivant les comportements des gaz de manière mathématique et théorique, Maxwell a apporté une perspective plus profonde qui a ouvert la voie à de nouvelles générations de physiciens, jetant les fondations pour la mécanique statistique moderne.
Contributions à l'Optique et à la Couleur
L'intérêt de Maxwell ne se limitait pas à l'électromagnétisme et à la thermodynamique. Il était également passionné par l'optique et la théorie des couleurs. En 1855, il a présenté son "Disque de Maxwell", une méthode expérimentale utilisant un disque rotatif divisé en segments de couleurs pour explorer la perception humaine des couleurs. Cette innovation l'a conduit à publier, en 1857, ses recherches sur la théorie des couleurs, où il a présenté les premières photographies en couleur grâce à la combinaison de trois filtres – rouge, vert et bleu – préfigurant la façon dont les couleurs sont actuellement reproduites dans les écrans électroniques.
Son travail dans ce domaine a jeté les bases de la théorie moderne des couleurs. En expliquant comment différentes longueurs d'onde de lumière correspondent à des perceptions distinctes de couleur, Maxwell a non seulement enrichi le domaine de l'optique, mais il a aussi offert un aperçu précieux sur le fonctionnement de l'œil humain et de la perception visuelle.
Le Mathématicien Visionnaire
En plus de ses contributions en physique, Maxwell a été un mathématicien prolifique. Ses compétences mathématiques ont permis d'élaborer des modèles théoriques avancés pour des phénomènes complexes, et cet aspect de son génie a influencé de nombreux domaines scientifiques. Il a rédigé divers travaux sur les surfaces courbes, les systèmes dynamiques, ainsi que sur les équations différentielles qui restent aujourd'hui encore étudiées par les chercheurs.
Maxwell a également joué un rôle central dans l'élaboration du pont de Wheatstone, un circuit utilisé pour mesurer des résistances électriques, démontrant son ingéniosité avec des composants pratiques aussi bien que théoriques. Sa capacité à aborder des problématiques de manière à la fois analytique et empirique en a fait une figure clé dont les méthodes résonnent encore à travers diverses disciplines scientifiques.
L'Héritage Éducatif de Maxwell
En plus d'être un chercheur, Maxwell se consacrait aussi à l'enseignement et au partage de la science. En 1871, il a accepté la chaire de professeur de physique expérimentale à l’Université de Cambridge, où il a fondé le laboratoire Cavendish, destiné à devenir un centre majeur de recherche en physique expérimentale. Sa passion pour l'avancement scientifique s'est reflétée dans le programme innovant qu'il y a institué, qui continue d'influencer les méthodes pédagogiques dans l’éducation scientifique aujourd'hui.
Maxwell était également un communicateur avisé, soucieux de rendre la science accessible au public. Il a souvent écrit pour des revues scientifiques de renom, expliquant des concepts complexes de manière compréhensible, et il a largement contribué à élever la stature de la science dans la société britannique de son époque.
Dans cette deuxième partie de notre article, nous avons exploré la richesse et la diversité des contributions de James Clerk Maxwell au-delà des équations électromagnétiques pour lesquelles il est le plus connu. En explorant ses travaux sur la théorie cinétique des gaz, l'optique, les mathématiques et l'éducation, il est clair que le spectre de l'influence de Maxwell s'étend bien au-delà des frontières de l'électromagnétisme, incarnant une étendue et une profondeur qui continuent d’inspirer et de renseigner le monde scientifique. Nous plongerons encore plus profondément dans sa vie et son héritage dans la troisième et dernière partie de cet article.
Le Défi de l'Éther Lumineux
L'un des défis scientifiques fascinants du XIXe siècle était l'explication du phénomène de propagation de la lumière. Maxwell, en intégrant la lumière dans le spectre des ondes électromagnétiques, a suscité des questions majeures concernant le milieu par lequel ces ondes se déplaçaient. À cette époque, l'hypothèse de l'éther lumineux était prédominante — un médium hypothétique supposé remplir l'espace et transmettre les ondes lumineuses.
Bien qu'il ait travaillé dans le cadre de cette hypothèse, Maxwell lui-même soulignait souvent les limitations de l'éther, reconnaissant que son existence n'avait jamais été prouvée. Plus tard, les expériences nulles de Michelson-Morley ont remis en question l'hypothèse de l'éther et ont ouvert la voie aux idées novatrices d'Albert Einstein sur la relativité restreinte. Bien que les implications complètes de la relativité soient survenues plusieurs décennies après sa mort, la vision de Maxwell, en tant que scientifique mettant continuellement à l'épreuve les théories existantes, a préparé le sol pour ces révolutions futures.
Maxwell et l'Ordinateur Moderne
Un aspect peu connu mais important de l'héritage de Maxwell est son impact indirect sur le développement de l'informatique moderne. Les lois de Maxwell ont inspiré les théories ultérieures qui ont guidé le développement des circuits électriques et des circuits intégrés. La compréhension des principes de la radioélectricité et leur application dans la transmission et la réception de signaux électriques sont des éléments fondamentaux de l'électronique numérique d'aujourd'hui.
Bien que Maxwell n'ait jamais travaillé directement sur des dispositifs électroniques, les principes établis par ses équations sous-tendent le fonctionnement des ordinateurs, smartphones et autres dispositifs électroniques de notre époque. Par extension, les nombreuses avancées dans la communication et l’information peuvent attribuer une partie de leur succès aux solides fondations qu'il a posées.
Sa Reconnaissance et Son Héritage
James Clerk Maxwell est aujourd'hui reconnu comme un géant de la science bien que, de son vivant, il n'ait pas toujours reçu l'attention méritée comparée à des contemporains tels que Charles Darwin et Michael Faraday. Il est encore possible de ressentir l'impact de ses découvertes dans les domaines les plus variés, de la physique théorique à la technologie appliquée, démontrant la portée intemporelle de son œuvre.
Son héritage perdure par le biais de divers hommages, tels que des musées à son nom et des congrès scientifiques dédiés à son travail. Les collèges, laboratoires et prix scientifiques continuent de célébrer sa vie et ses contributions, inspirant de nouvelles générations de scientifiques à explorer les frontières de la connaissance humaine avec le même esprit de curiosité et d'innovation que Maxwell incarnait.
Maxwell dans la Culture Contemporaine
En dépit de sa stature dans le monde scientifique, Maxwell est souvent absent du grand livre des personnages historiques immédiatement reconnus par le public général. Cependant, son influence se fait sentir sur de nombreuses facettes culturelles et technologiques de notre quotidien. Par le biais des technologies de communication, il connecte le monde d'une manière que peu de scientifiques avant ou depuis ont réalisée.
Des documentaires, livres et conférences tentent de redonner à Maxwell la place qui lui revient dans le panthéon des grandes figures scientifiques. Chaque fois que nous communiquons par Wi-Fi, utilisons la technologie GPS, ou même allumons une ampoule, nous faisons appel indirectement aux lois qu'il a déduites et qui ont transformé notre monde.
Conclusion : Le Vaste Horizon d'une Vision Géniale
Alors que nous clôturons cet article, il est évident que James Clerk Maxwell était bien plus qu'un simple mathématicien ou physicien ; il était un visionnaire dont la portée de pensée a transcendé son époque. Ses découvertes ont non seulement fondamentalement changé la physique, mais elles ont aussi eu un impact durable et omniprésent dans notre vie quotidienne moderne.
Son exemple nous rappelle que la curiosité intellectuelle et l'innovation sont les piliers fondamentaux du progrès, nous incitant à respecter et à redécouvrir ces figures historiques qui, à travers leur génie, continuent de transformer notre réalité pour toujours. Par ses nombreux travaux, James Clerk Maxwell reste un phare qui guide les nouvelles générations vers l'inconnu et le possible.






