Évariste Galois: Mathematisches Genie und tragischer Held
Évariste Galois war ein französisches mathematisches Genie, dessen bahnbrechende Arbeiten die moderne Algebra begründeten. Sein Leben war geprägt von persönlichen Tragödien und politischen Wirren, die in einem tödlichen Duell mit nur 20 Jahren endeten. Dennoch hinterließ er mit der Galoistheorie ein Vermächtnis, das die Mathematik bis heute prägt.
Das kurze Leben eines mathematischen Revolutionärs
Évariste Galois wurde am 25. Oktober 1811 in Bourg-la-Reine bei Paris geboren. Sein Vater, Nicolas-Gabriel Galois, diente als Bürgermeister der kleinen Gemeinde. Die Familie lebte in einer politisch turbulenten Zeit der Restauration nach Napoleon Bonaparte.
Die frühen Jahre von Galois waren von familiären Schicksalsschlägen überschattet. Sein Vater beging 1829 Selbstmord, nachdem er in politische Intrigen verwickelt worden war. Dieser Verlust stürzte den jungen Évariste in eine tiefe Krise und prägte seine rebellische Haltung.
Ausbildung und erste mathematische Erfolge
Galois besuchte das renommierte Collège Louis-le-Grand in Paris, wo sein außergewöhnliches Talent früh erkannt wurde. Bereits mit 17 Jahren veröffentlichte er seine erste mathematische Arbeit über Kettenbrüche. Sein mathematischer Geist entwickelte sich rasant, doch seine akademische Laufbahn verlief alles andere als glatt.
Zweimal scheiterte er an der Aufnahmeprüfung der Eliteuniversität École polytechnique, was ihn zutiefst frustrierte. Stattdessen studierte er an der École normale supérieure, wo er seine revolutionären Ideen zur Gleichungstheorie weiterentwickelte.
Die Geburt der Galoistheorie
Galois' größte Leistung war die Entwicklung der nach ihm benannten Galoistheorie. Dieser innovative Ansatz revolutionierte das Verständnis algebraischer Gleichungen grundlegend. Seine Arbeit lieferte nicht nur elegante Beweise, sondern schuf völlig neue mathematische Konzepte.
Die Galoistheorie untersucht die Symmetrien von Polynomgleichungen durch die Zuordnung von Gruppen zu Polynomen. Diese abstrakte Betrachtungsweise ermöglichte tiefe Einsichten in die Lösbarkeit von Gleichungen.
Der Beweis der Unlösbarkeit höherer Gleichungen
Eine der bedeutendsten Entdeckungen von Galois war der rigorose Beweis, dass algebraische Gleichungen fünften oder höheren Grades keine allgemeine Lösungsformel in Radikalen besitzen. Damit bestätigte und erweiterte er die Arbeiten von Niels Henrik Abel und Paolo Ruffini.
Sein Lösbarkeitskriterium charakterisiert genau, welche Gleichungen durch Radikale auflösbar sind. Dieser Durchbruch markierte einen Wendepunkt in der Entwicklung der modernen Algebra.
In der Nacht vor seinem tödlichen Duell schrieb Galois hastig seine wichtigsten mathematischen Ideen nieder, um sein wissenschaftliches Erbe zu sichern.
Politisches Engagement und Verfolgung
Neben seiner mathematischen Arbeit war Galois auch politisch aktiv. Als überzeugter Republikaner engagierte er sich in der Julirevolution von 1830. Seine radikalen politischen Ansichten brachten ihn wiederholt in Konflikt mit den Behörden.
Wegen seiner politischen Aktivitäten wurde Galois zweimal inhaftiert, zuletzt für neun Monate von Juli 1831 bis April 1832. Selbst im Gefängnis setzte er seine mathematischen Forschungen fort und entwickelte seine Theorien weiter.
Die Ablehnung durch die wissenschaftliche Establishment
Die Académie des Sciences lehnte Galois' Manuskripte mehrfach ab – teils wegen ihrer mangelnden Verständlichkeit, teils weil sie als zu revolutionär galten. Diese Zurückweisungen verstärkten seine Frustration mit dem etablierten Wissenschaftsbetrieb.
Augustin-Louis Cauchy, einer der führenden Mathematiker seiner Zeit, verlor sogar eines von Galois' eingereichten Manuskripten. Diese Erfahrungen prägten Galois' zynische Haltung gegenüber der akademischen Welt.
Das tragische Ende eines jungen Genies
Am 31. Mai 1832 erlag Galois im Alter von nur 20 Jahren den Verletzungen aus einem Duell. Die genauen Umstände des Duells bleiben bis heute rätselhaft. Mögliche Gründe reichen von unglücklicher Liebe bis zu politischen Intrigen.
Am Vorabend des Duells schrieb Galois in einem berühmt gewordenen Brief an seinen Freund Auguste Chevalier seine letzten mathematischen Einsichten nieder. Diese "Testamentsschrift" sicherte seine Unsterblichkeit in der Mathematik.
- 25. Oktober 1811: Geburt in Bourg-la-Reine
- 1829: Erste Veröffentlichung mathematischer Arbeiten
- 1830: Politisches Engagement in der Julirevolution
- 1831-1832: Inhaftierung wegen politischer Aktivitäten
- 31. Mai 1832: Tod nach einem Duell
Obwohl Galois nur 20 Jahre alt wurde, hinterließ er ein mathematisches Vermächtnis, das die Algebra für immer verändern sollte. Seine Ideen waren ihrer Zeit so weit voraus, dass ihre volle Bedeutung erst Jahre nach seinem Tod erkannt wurde.
Mathematische Schlüsselkonzepte und Innovationen
Galois führte mehrere bahnbrechende Konzepte in die Mathematik ein, die heute fundamental sind. Die Galoistheorie verbindet Gruppentheorie mit Körpertheorie und bietet ein mächtiges Werkzeug zur Untersuchung von Polynomgleichungen.
Seine Arbeit legte den Grundstein für viele moderne mathematische Disziplinen. Besonders bedeutsam war die Einführung der Galoiskörper (auch endliche Körper oder GF(q) genannt), die heute in vielen Anwendungen crucial sind.
Die Bedeutung der Gruppentheorie
Galois erkannte als einer der Ersten die fundamentale Bedeutung von Gruppen in der Mathematik. Seine Zuordnung von Gruppen zu Polynomen ermöglichte eine systematische Klassifikation von Gleichungen nach ihrer Lösbarkeit.
Dieser Ansatz revolutionierte nicht nur die Algebra, sondern beeinflusste später auch andere Bereiche der Mathematik und Physik. Die Gruppentheorie wurde zu einem unverzichtbaren Werkzeug in der modernen Mathematik.
Die Tragik seines kurzen Lebens und die Größe seines mathematischen Vermächtnisses machen Évariste Galois zu einer der faszinierendsten Figuren der Wissenschaftsgeschichte. Sein Werk bleibt bis heute aktuell und inspirierend für Mathematiker weltweit.
Die wissenschaftliche Anerkennung nach Galois' Tod
Die Bedeutung von Galois' Werk wurde zu seinen Lebzeiten kaum erkannt. Erst Jahre nach seinem frühen Tod begann die mathematische Gemeinschaft die Tiefe seiner Entdeckungen zu verstehen. Der französische Mathematiker Joseph Liouville spielte eine Schlüsselrolle bei der postumen Veröffentlichung seiner Arbeiten.
1846 veröffentlichte Liouville Galois' gesammelte Schriften im Journal de Mathématiques Pures et Appliquées. Diese Veröffentlichung markierte den Beginn der internationalen Anerkennung für das mathematische Genie. Die Fachwelt erkannte allmählich die revolutionäre Natur seiner Ideen.
Die Rezeption durch zeitgenössische Mathematiker
Anfangs stießen Galois' abstrakte Konzepte auf Skepsis und Unverständnis. Seine Verwendung von Gruppen war seiner Zeit so weit voraus, dass selbst erfahrene Mathematiker Schwierigkeiten hatten, seine Argumentation zu folgen. Dies änderte sich erst mit der Entwicklung der abstrakten Algebra im späten 19. Jahrhundert.
Mathematiker wie Camille Jordan und später Emmy Noether erkannten die volle Tragweite von Galois' Arbeit. Sie entwickelten seine Ideen weiter und integrierten sie in das Fundament der modernen Mathematik.
"Galois hatte die Gabe, die tiefsten Probleme der Algebra mit einer Klarheit und Kühnheit anzupacken, die bewundernswert ist." - Joseph Liouville
Die Galoistheorie: Grundlagen und Prinzipien
Die Galoistheorie stellt eine tiefgründige Verbindung zwischen Körpertheorie und Gruppentheorie her. Sie untersucht Symmetrien von algebraischen Gleichungen durch die Analyse von Körpererweiterungen. Dieser elegante Ansatz löst fundamentale Probleme der Algebra.
Das zentrale Konzept ist die Galoisgruppe, die die Symmetrien einer Körpererweiterung beschreibt. Je einfacher die Gruppenstruktur, desto einfacher ist die zugrunde liegende Gleichung lösbar. Diese Erkenntnis revolutionierte das Verständnis algebraischer Gleichungen.
Das Haupttheorem der Galoistheorie
Das Haupttheorem der Galoistheorie stellt eine Bijektion zwischen Zwischenkörpern einer Galoiserweiterung und Untergruppen der Galoisgruppe her. Dieser fundamentale Satz ermöglicht die Übersetzung algebraischer Probleme in gruppentheoretische Fragestellungen.
Die Eleganz dieses Ansatzes liegt in der Reduktion komplexer algebraischer Probleme auf die Untersuchung von Gruppenstrukturen. Dies eröffnete völlig neue Perspektiven in der Gleichungstheorie und darüber hinaus.
Anwendungen auf Polynomgleichungen
Galois' Theorie liefert ein effektives Kriterium für die Lösbarkeit von Gleichungen durch Radikale. Eine Gleichung ist genau dann durch Radikale lösbar, wenn ihre Galoisgruppe auflösbar ist. Dies klärte endgültig das jahrhundertealte Problem der Lösbarkeit von Gleichungen.
Der Beweis der Unlösbarkeit der allgemeinen Gleichung fünften Grades war eine der spektakulärsten Anwendungen dieser Theorie. Galois zeigte, dass die Galoisgruppe der allgemeinen Gleichung n-ten Grades für n ≥ 5 die volle symmetrische Gruppe ist.
Moderne Anwendungen der Galoistheorie
Die Bedeutung der Galoistheorie beschränkt sich nicht auf die reine Mathematik. Ihre Konzepte finden heute breite Anwendung in verschiedenen wissenschaftlichen Disziplinen. Besonders bedeutsam sind ihre Beiträge zur modernen Kryptographie und Kodierungstheorie.
In der Quanteninformatik spielen Galois-Körper eine wichtige Rolle bei Fehlerkorrekturverfahren. Die Theorie endlicher Körper, die auf Galois' Arbeit basiert, ist fundamental für viele digitale Technologien.
Anwendungen in der Kryptographie
Endliche Körper (Galois-Körper) bilden die Grundlage vieler moderner Verschlüsselungsverfahren. Algorithmen wie der Advanced Encryption Standard (AES) nutzen Operationen in GF(2^8). Diese Anwendung sichert heute milliardenfach täglich digitale Kommunikation.
Die Sicherheit vieler kryptographischer Protokolle basiert auf der Schwierigkeit diskreter Logarithmenprobleme in endlichen Körpern. Galois' Pionierarbeit lieferte damit unintendiert die mathematische Grundlage für die digitale Sicherheit des 21. Jahrhunderts.
- Verschlüsselungsalgorithmen: AES, Diffie-Hellman, elliptische Kurven-Kryptographie
- Fehlerkorrektur-Codes: Reed-Solomon-Codes in CDs, DVDs und QR-Codes
- Digitale Signaturen: RSA und andere Public-Key-Verfahren
Beiträge zur Zahlentheorie
Die Galoistheorie revolutionierte auch die algebraische Zahlentheorie. Das Konzept der Galois-Darstellungen spielt eine zentrale Rolle im Beweis des Großen Fermatschen Satzes durch Andrew Wiles. Diese Darstellungen verbinden Zahlentheorie mit Analysis und Geometrie.
In der arithmetischen Geometrie ermöglicht die Galoistheorie tiefe Einsichten in die Struktur algebraischer Varietäten über Zahlkörpern. Diese Verbindung zwischen Algebra und Geometrie erweist sich als äußerst fruchtbar für moderne mathematische Forschung.
Galois' Einfluss auf die moderne Mathematik
Galois' Ideen legten den Grundstein für die Entwicklung der abstrakten Algebra im 20. Jahrhundert. Seine Betonung struktureller Eigenschaften anstelle konkreter Berechnungen ebnete den Weg für einen neuen mathematischen Stil. Dieser strukturelle Ansatz prägt die moderne Mathematik bis heute.
Die Konzepte der Gruppentheorie, die Galois einführte, wurden zu einem universellen Werkzeug in der Mathematik. Von der Topologie bis zur Quantenphysik finden Gruppen Anwendung in den verschiedensten Disziplinen.
Die Entwicklung der algebraischen Strukturen
Galois' Arbeit inspirierte die systematische Untersuchung algebraischer Strukturen wie Gruppen, Ringe und Körper. Diese Strukturen bilden heute das Fundament der modernen Algebra. Mathematiker wie David Hilbert und Emmy Noether entwickelten diesen Ansatz weiter.
Die axiomatische Methode, die Galois implizit anwandte, wurde zum Standard in der modernen Mathematik. Sein Fokus auf abstrakte Symmetrien statt konkreter Lösungen eröffnete neue Perspektiven.
Einfluss auf die mathematische Physik
Die von Galois begründete Gruppentheorie erwies sich als essentiell für die moderne Physik. In der Quantenmechanik beschreiben Gruppen Symmetrien von Elementarteilchen. Die Klassifikation elementarer Teilchen basiert auf Darstellungstheorie von Lie-Gruppen.
Auch in der Festkörperphysik spielen Raumgruppen eine cruciale Rolle bei der Beschreibung kristalliner Strukturen. Galois' Erbe reicht damit weit über die reine Mathematik hinaus.
Die Galoistheorie stellt eines der schönsten Beispiele dar, wie abstrakte mathematische Konzepte unerwartete praktische Anwendungen finden können.
Die anhaltende Relevanz von Galois' Werk zeigt sich in zahlreichen aktuellen Forschungsgebieten. Von der arithmetischen Geometrie bis zur topologischen Gruppentheorie inspiriert sein Denken weiterhin neue mathematische Entwicklungen.
Das kulturelle Erbe und die Rezeption von Galois
Das Leben und Werk von Évariste Galois hat zahlreiche Künstler, Schriftsteller und Filmemacher inspiriert. Seine dramatische Lebensgeschichte mit ihrem tragischen Ende fasziniert bis heute. Mehrere Biografien und Romane wurden über das mathematische Wunderkind veröffentlicht.
Im Jahr 2011, zum 200. Geburtstag von Galois, fanden weltweit Gedenkveranstaltungen und Konferenzen statt. Mathematiker würdigten sein Erbe mit speziellen Publikationen und Vorträgen. Diese Aktivitäten unterstreichen die anhaltende Bedeutung seines Werkes.
Galois in Literatur und Populärkultur
Autoren wie Leopold Infeld und Jean-Pierre Gauthier widmeten Galois biografische Romane. Diese Werke popularisieren sein Leben für ein breiteres Publikum. Selbst in Science-Fiction und Theaterstücken tauchen Referenzen zu seinem Werk auf.
Podcasts und Dokumentationen beleuchten regelmäßig sein faszinierendes Schicksal. Formate wie "Geschichten aus der Mathematik" machen seine komplexen Ideen einer breiten Öffentlichkeit zugänglich. Diese populärwissenschaftliche Aufarbeitung sichert sein Andenken.
Aktuelle Forschung auf Basis von Galois' Werk
Die Galoistheorie bleibt ein aktives Forschungsgebiet in der modernen Mathematik. Zahlreiche Mathematiker arbeiten an Verallgemeinerungen und Erweiterungen seiner ursprünglichen Ideen. Besonders die inverse Galoistheorie stellt ein wichtiges aktuelles Forschungsfeld dar.
Dieses Gebiet untersucht, welche Gruppen als Galoisgruppen über gegebenen Zahlkörpern realisiert werden können. Das Problem ist trotz jahrzehntelanger Forschung noch nicht vollständig gelöst. Es verbindet Zahlentheorie mit Gruppentheorie auf tiefgründige Weise.
Fortschritte in der arithmetischen Geometrie
Moderne Forschungsrichtungen wie die arithmetische Geometrie bauen direkt auf Galois' Ideen auf. Die Galois-Kohomologie spielt eine zentrale Rolle beim Studium algebraischer Varietäten. Diese Verbindung zwischen Algebra und Geometrie erweist sich als äußerst fruchtbar.
Forscher untersuchen Galois-Darstellungen, um tiefe arithmetische Eigenschaften zu verstehen. Der Beweis der Modularitätsvermutung durch Andrew Wiles nutzte solche Darstellungen wesentlich. Dies zeigt die anhaltende Relevanz von Galois' Ansätzen.
Anwendungen in der Informatik
In der Theoretischen Informatik finden Galois-Verbindungen Anwendung in der Ordnungstheorie. Diese Konzepte helfen bei der Formalisierung von Abstraktionen in Programmen. Galois' Ideen inspirieren sogar Forschung in künstlicher Intelligenz.
Die Untersuchung von Symmetriegruppen hilft beim Verständnis von Transformationsinvarianten in maschinellem Lernen. Diese unerwarteten Anwendungen zeigen die Universalität von Galois' mathematischem Denken.
"Galois' Genie lag in seiner Fähigkeit, die Essenz mathematischer Probleme zu erkennen und durch Abstraktion zu lösen." - Moderne Mathematikhistoriker
Die pädagogische Bedeutung von Galois' Werk
Die Galoistheorie bildet heute einen zentralen Bestandteil des Mathematikstudiums an Universitäten weltweit. Sie wird typischerweise in Fortgeschrittenenkursen zur Algebra unterrichtet. Das Verständnis dieser Theorie gilt als Meilenstein in der mathematischen Ausbildung.
Lehrbücher zur Algebra widmen Galois' Werk umfangreiche Kapitel. Seine eleganten Beweise und konzeptionellen Durchbrüche dienen als Lehrbeispiele mathematischer Kreativität. Studierende lernen an seiner Arbeit das Denken in Strukturen.
Vermittlung in Schulen und Hochschulen
Auch in der Schulmathematik finden Elemente der Galoistheorie Erwähnung. Die Unlösbarkeit der Gleichungen fünften Grades fasziniert begabte Schüler. Didaktische Aufbereitungen machen seine Ideen für junge Mathematiker zugänglich.
An vielen Universitäten werden spezielle Seminare zu Galois' Leben und Werk angeboten. Diese Kurse verbinden mathematische Inhalte mit wissenschaftshistorischen Betrachtungen. Sie zeigen die menschliche Seite der Mathematik.
- Bachelorstudiengänge: Einführung in die Galoistheorie im dritten Jahr
- Masterprogramme: Vertiefte Behandlung mit modernen Anwendungen
- Promotionsforschung: Spezialisierung auf aktuelle Forschungsfragen
Zukunftsaussichten und Entwicklungspotential
Die Forschung auf Basis von Galois' Werk zeigt keine Anzeichen einer Verlangsamung. Im Gegenteil: Neue Verbindungen zu anderen mathematischen Gebieten werden ständig entdeckt. Die Langlands-Programm stellt eine tiefgründige Verallgemeinerung der Galoistheorie dar.
Dieses ambitionierte Forschungsprogramm verbindet Zahlentheorie mit Darstellungstheorie. Es zählt zu den bedeutendsten ungelösten Problemen der modernen Mathematik. Galois' Ideen bilden hierfür das konzeptionelle Fundament.
Quantencomputing und neue Anwendungen
Im Bereich des Quantencomputing könnten Galois-Körper neue Anwendungen finden. Quantenalgorithmen für diskrete Logarithmen in endlichen Körpern sind ein aktives Forschungsgebiet. Diese Arbeiten könnten die Kryptographie revolutionieren.
Die Untersuchung von Galois-Darstellungen in quantenmechanischen Systemen eröffnet neue Perspektiven. Solche interdisziplinären Ansätze zeigen das Potential von Galois' Erbe für zukünftige Entdeckungen.
Das Vermächtnis eines mathematischen Genies
Évariste Galois hinterließ trotz seines kurzen Lebens ein unvergessliches Vermächtnis. Seine revolutionären Ideen veränderten die Mathematik grundlegend und öffneten Türen zu neuen Forschungsgebieten. Die Galoistheorie gehört zu den tiefgründigsten und elegantesten Konstruktionen der Mathematik.
Sein Leben steht beispielhaft für die Kraft mathematischer Intuition und den Wert wissenschaftlicher Unabhängigkeit. Trotz zahlreicher Rückschläge verfolgte er unbeirrt seine visionären Ideen. Diese Beharrlichkeit inspiriert Mathematiker bis heute.
Die zeitlose Bedeutung seiner Arbeit
Galois' Werk demonstriert die Schönheit und Effektivität abstrakten Denkens. Seine Fähigkeit, komplexe Probleme durch strukturelle Analyse zu lösen, bleibt vorbildhaft. Diese methodische Innovation prägte die gesamte spätere Mathematik.
Die Universalität seiner Ansätze zeigt sich in den vielfältigen Anwendungen seiner Theorie. Von der Kryptographie bis zur Teilchenphysik finden seine Konzepte Verwendung. Diese Breite der Anwendungen ist bemerkenswert.
"In der Geschichte der Mathematik gibt es wenige Figuren, deren Werk so nachhaltig und vielfältig gewirkt hat wie das von Évariste Galois." - Mathematics Today
Zusammenfassung und abschließende Betrachtung
Das Leben und Werk von Évariste Galois vereint tragische Elemente mit mathematischer Genialität in einzigartiger Weise. Sein kurzes Leben von nur 20 Jahren reichte aus, um die Algebra für immer zu verändern. Die Galoistheorie stellt einen Meilenstein in der Geschichte der Mathematik dar.
Seine konzeptionellen Durchbrüche legten den Grundstein für die moderne Algebra und beeinflussten zahlreiche andere Gebiete. Die anhaltende Relevanz seiner Arbeit zeigt sich in aktueller Forschung und praktischen Anwendungen.
Hauptleistungen im Überblick
- Begründung der Galoistheorie als Verbindung von Gruppen- und Körpertheorie
- Rigoroser Beweis der Unlösbarkeit allgemeiner Gleichungen fünften und höheren Grades
- Entwicklung des Lösbarkeitskriteriums für polynomiale Gleichungen
- Einführung fundamentaler Konzepte wie Galoisgruppe und Galois-Körper
- Inspiration für moderne Forschungsgebiete wie Kryptographie und Quantencomputing
Évariste Galois bleibt eine Ikone der Mathematik, deren Werk Generationen von Wissenschaftlern inspiriert hat. Seine Geschichte erinnert daran, dass wissenschaftlicher Fortschritt oft von unkonventionellem Denken und persönlichem Mut abhängt. Trotz seines tragischen Endes lebt sein mathematisches Erbe weiter und entwickelt sich ständig weiter.
Die Faszination für sein Werk und sein Schicksal wird auch in Zukunft ungebrochen bleiben. Neue Generationen von Mathematikern werden an seinen Ideen anknüpfen und sie in unerwartete Richtungen weiterentwickeln. Das Vermächtnis von Galois ist damit nicht nur historisch bedeutsam, sondern lebendig und zukunftsweisend.


Vercingetorix: Der Gallische Held und seine Revolte gegen Rom
Einleitung: Wer war Vercingetorix?
Vercingetorix gilt als einer der bekanntesten Krieger und Anführer der gallischen Stämme, der im 1. Jahrhundert v. Chr. einen großen Aufstand gegen die römische Expansion unter Julius Caesar anzettelte. Sein Name bedeutet übersetzt „großer König der Krieger“ – eine Bezeichnung, die seine Rolle als charismatischer und strategischer Führer unterstreicht. Obwohl er letztlich scheiterte und seine Niederlage das Ende der gallischen Unabhängigkeit markierte, bleibt er bis heute eine Symbolfigur des Widerstands und des Kampfes für die Freiheit.
Die frühen Jahre und der Aufstieg zum Anführer
Vercingetorix wurde um 82 v. Chr. als Sohn eines einflussreichen Adligen des keltischen Stammes der Arverner geboren. Sein Vater, Celtillus, hatte versucht, eine Allianz der gallischen Stämme zu schmieden, wurde jedoch von seinen eigenen Leuten hingerichtet, als er zu mächtig wurde. Dieses Schicksal prägte den jungen Vercingetorix, der bereits früh politische Taktiken und die Machtdynamik zwischen den Stämmen lernte.
Im Jahr 52 v. Chr., als Julius Caesar mit seinen römischen Legionen Gallien immer weiter unterwarf, gelang es Vercingetorix, die zerstrittenen Stämme zu einen. Mit überzeugender Rhetorik und militärischem Geschick wurde er zum Oberbefehlshaber der gallischen Koalition gewählt. Sein Plan: Eine vereinte Front gegen Rom zu bilden und die Besatzungstruppen aus dem Land zu vertreiben.
Strategie und Taktik der gallischen Revolte
Vercingetorix setzte auf eine Guerilla-Taktik, die den Römern großen Schaden zufügte. Anstatt sich auf offene Schlachten einzulassen, befahl er seinen Truppen, römische Versorgungslinien anzugreifen, Brücken zu zerstören und Dörfer niederzubrennen, um dem Feind keine Ressourcen zu hinterlassen. Diese „Verbrannte Erde“-Strategie zwang Caesar zu einer defensiveren Haltung.
Einer der entscheidenden Momente des Krieges war die Belagerung von Avaricum (heute Bourges). Obwohl die Stadt letztlich fiel und ein Massaker an den Bewohnern folgte, zeigte Vercingetorix’ Entschlossenheit, dass die Gallier bereit waren, hohe Opfer für ihre Freiheit zu bringen.
Die Schlacht von Gergovia
Ein großer Sieg gelang Vercingetorix in der Schlacht von Gergovia (Juni 52 v. Chr.), wo er Caesars Truppen eine empfindliche Niederlage zufügte. Er nutzte die Höhenlage der Festung aus und lockte die Römer in einen Hinterhalt. Dieser Triumph stärkte seine Position und brachte weitere Stämme auf seine Seite.
Doch obwohl die Gallier taktisch klug vorgingen, fehlte es ihnen an der langfristigen Logistik und Disziplin der römischen Armee. Caesar, ein Meister der Kriegsführung, begann, seine Legionen neu zu organisieren und Gegenangriffe zu planen.
Die Niederlage von Alesia und das Ende des Widerstands
Der Wendepunkt des Krieges kam mit der Belagerung von Alesia (September 52 v. Chr.). Vercingetorix hatte sich in die befestigte Stadt zurückgezogen, während Caesar ein riesiges Belagerungswerk errichtete – bestehend aus Wällen, Gräben und Türmen. Als gallische Entsatztruppen versuchten, die Römer von außen anzugreifen, scheiterte ihr koordinierter Angriff.
Letztlich musste sich Vercingetorix ergeben. Die Legende besagt, dass er in voller Rüstung zu Caesar ritt und seine Waffen zu dessen Füßen niederlegte. Er wurde gefangen genommen und später in Rom als Kriegstrophäe vorgeführt, bevor man ihn hinrichtete.
Die Bedeutung von Vercingetorix‘ Erbe
Obwohl sein Aufstand scheiterte, wurde Vercingetorix zu einem nationalen Mythos Frankreichs. Im 19. Jahrhundert, als Frankreich nach einer Identität jenseits der Monarchie suchte, wurde er als Symbol des Widerstands gegen Fremdherrschaft wiederentdeckt. Sein Vermächtnis lebt in Büchern, Denkmälern und sogar in modernen politischen Diskursen weiter.
Fazit des ersten Teils
Vercingetorix‘ Geschichte ist eine von Mut, Strategie und tragischem Scheitern. Sein Kampf gegen Rom zeigt die Herausforderungen, mit denen unterlegene Völker gegen übermächtige Imperien kämpfen. Doch sein Name bleibt als Inbegriff des Freiheitswillens in Erinnerung.
(Fortsetzung folgt)
Die Rolle der gallischen Stämme im Konflikt mit Rom
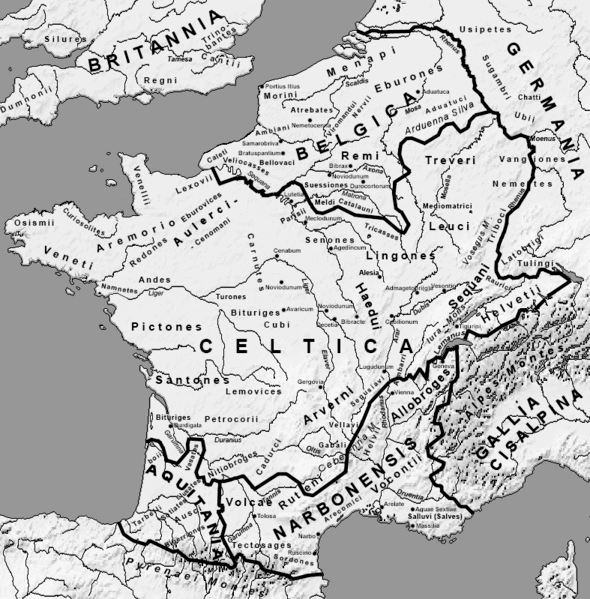
Gallien war zur Zeit von Vercingetorix kein geeintes Königreich, sondern ein Flickenteppich verschiedener keltischer Stämme, die oft untereinander in Fehden lagen. Die Arverner, der Stamm des Vercingetorix, gehörten zu den mächtigsten, doch erst durch die Bedrohung Roms gelang es, eine gemeinsame Front zu bilden. Andere wichtige Stämme wie die Häduer, die Senonen oder die Biturigen schwankten zwischen Bündnis mit Rom und Aufstand – eine Unsicherheit, die sowohl Caesar als auch Vercingetorix auszunutzen versuchten.
Interessant ist, dass einige gallische Adlige sogar mit den Römern kollaborierten, um eigene Machtinteressen durchzusetzen. Die Häduer etwa, traditionelle Rivalen der Arverner, verbündeten sich zeitweise mit Caesar, um ihre Position zu stärken. Dies zeigt, dass der Krieg nicht nur ein Kampf zwischen Galliern und Römern war, sondern auch interne Machtkämpfe widerspiegelte.
Die Bedeutung von Diplomatie und Propaganda
Vercingetorix verstand, dass ein militärischer Sieg allein nicht ausreichen würde. Er setzte auf psychologische Kriegsführung und Diplomatie, um Stämme auf seine Seite zu ziehen. Geschickt nutzte er die Furcht vor römischer Unterdrückung und appellierte an den gemeinsamen gallischen Stolz. Caesar hingegen spielte die Stämme gegeneinander aus, versprach Belohnungen für Loyalität und bestrafte Aufständische grausam.
Diese Dynamik macht deutlich, wie komplex der Konflikt war: Nicht nur Schlachten wurden auf dem Feld geschlagen, sondern auch in den Versammlungen der Druiden und den Höfen der Stammesführer.
Die militärischen Stärken und Schwächen der Gallier
Die gallischen Krieger waren für ihre Tapferkeit und ihren Kampfesmut berühmt. Mit langen Schwertern, Speeren und Schilden ausgestattet, waren sie in direkten Kämpfen gefürchtet. Allerdings fehlte es ihnen an Disziplin und strategischer Planung im großen Stil. Während die Römer in Formationen kämpften und Befehle präzise befolgten, neigten die Gallier zu spontanen Angriffen, was Caesar mehrfach ausnutzte.
Ein weiterer Nachteil war die mangelnde Logistik. Die Römer hatten ein ausgeklügeltes Versorgungssystem mit Nachschubrouten, während die gallischen Armeen oft von lokalen Ressourcen abhingen – ein Problem, besonders während Belagerungen.
Die Technologischen Unterschiede
Roms militärischer Vorteil lag auch in der technischen Überlegenheit. Die Legionäre verfügten über standardisierte Waffen, schwere Belagerungsmaschinen und gut ausgebaute Straßen für schnelle Truppenbewegungen. Die Gallier hingegen setzten auf individuelle Kampfkunst und improvisierte Taktiken.
Trotzdem zeigte Vercingetorix‘ Guerilla-Krieg, dass Flexibilität eine wirksame Waffe sein konnte. Seine schnellen Überfälle auf römische Nachschubkolonnen zwangen Caesar sogar zeitweise zum Rückzug.
Julius Caesar: Der Gegenspieler des Vercingetorix
Ohne die Figur des Julius Caesar wäre die Geschichte Vercingetorix‘ nicht vollständig. Caesar war nicht nur ein brillanter Feldherr, sondern auch ein Meister der politischen Manipulation. Sein Werk „De Bello Gallico“ (Der Gallische Krieg) diente nicht nur als militärischer Bericht, sondern auch als Propagandaschrift, um seinen Ruhm in Rom zu mehren.
Interessanterweise lobte Caesar in seinen Schriften sogar die Fähigkeiten des Vercingetorix – wohl auch, um seinen eigenen Sieg noch größer erscheinen zu lassen. Diese ambivalente Bewunderung zwischen Feinden ist ein faszinierender Aspekt ihres Konflikts.
Caesars Taktiken gegen die gallische Revolte
Caesars Erfolg beruhte auf mehreren Faktoren:
- **Schnelle Mobilität* Er teilte seine Legionen auf, um gleichzeitig an mehreren Fronten zu operieren.
- **Belagerungskunst* Die Konstruktion von Befestigungen wie in Alesia war eine seiner Spezialitäten.
- **Psychologische Kriegsführung* Durch gezielte Grausamkeit (etwa das Massaker von Avaricum) schüchterte er Gegner ein.
Doch auch Caesar machte Fehler. Die Niederlage bei Gergovia zeigte, dass selbst er verwundbar war, wenn er die Entschlossenheit seiner Feinde unterschätzte.
Die gesellschaftlichen Auswirkungen des Krieges
Der gallische Krieg veränderte nicht nur die politische Landkarte, sondern hatte auch tiefgreifende soziale Folgen. Schätzungsweise eine Million Gallier starben, weitere Million wurden versklavt. Ganze Regionen wurden entvölkert, während römische Siedler und Veteranen das Land übernahmen.
Für Rom wiederum war der Sieg über Gallien ein entscheidender Schritt zur Weltmacht. Die eroberten Ressourcen – Gold, landwirtschaftliche Güter, Sklaven – stärkten die Wirtschaft und finanzierten Caesars spätere Machtkämpfe in Rom.
Kultureller Wandel in Gallien
Nach der Eroberung begann die Romanisierung der gallischen Gebiete. Latein verdrängte allmählich die keltischen Sprachen, römische Städte entstanden, und die lokalen Eliten passten sich an, um ihre Macht zu erhalten. Doch viele gallische Traditionen lebten unter der Oberfläche weiter – ein Phänomen, das bis heute in französischer Folklore und regionalen Bräuchen spürbar ist.
Die letzten Tage des Vercingetorix
Nach seiner Gefangennahme in Alesia wurde Vercingetorix sechs Jahre lang in einem römischen Kerker festgehalten, bevor er 46 v. Chr. im Gefolge von Caesars Triumphzug durch Rom öffentlich vorgeführt und anschließend erwürgt wurde. Dieses grausame Ende unterstrich Roms Absicht, jeden Widerstand endgültig zu brechen.
Doch selbst in der Niederlage wurde Vercingetorix zur Legende. Sein Stolz und seine Weigerung, um Gnade zu bitten, beeindruckten sogar seine Feinde. In dieser Hinsicht war sein Tod nicht das Ende, sondern der Beginn eines Mythos, der die Jahrhunderte überdauern sollte.
Historische Quellen und ihre Verzerrungen
Unser Wissen über Vercingetorix stammt fast ausschließlich aus römischen Quellen – vor allem Caesars „De Bello Gallico“. Diese einseitige Überlieferung macht es schwer, die gallische Perspektive vollständig zu rekonstruieren. Moderne Archäologie hilft zwar, ein klareres Bild zu zeichnen, aber viele Fragen bleiben offen: Wie sah die Gesellschaft der Gallier wirklich aus? Wie entschieden sich Stämme für oder gegen Bündnisse?
Diese Wissenslücken machen Vercingetorix zugleich zu einer geheimnisvollen Figur, deren wahre Persönlichkeit wohl für immer Teil der Spekulation bleiben wird.
Zwischenfazit: Ein Kampf mit Langzeitfolgen
Der Aufstand des Vercingetorix war mehr als eine militärische Auseinandersetzung – er markierte den Zusammenprall zweier Kulturen und den Beginn einer neuen Ära für Gallien. Während Rom gestärkt daraus hervorging, wurde die keltische Welt nachhaltig verändert. Doch der Geist des Widerstands, den Vercingetorix verkörperte, lebte in Mythen und Geschichten weiter und inspiriert bis heute.
(Fortsetzung folgt)
Vercingetorix im kollektiven Gedächtnis: Mythen und moderne Rezeption
Nach seinem Tod verschwand Vercingetorix zunächst aus der offiziellen Geschichtsschreibung, doch im 19. Jahrhundert erlebte seine Figur eine bemerkenswerte Wiedergeburt. Während der Französischen Revolution und vor allem unter Napoleon III. wurde der gallische Held als Symbol nationaler Einheit und Widerstandskraft wiederentdeckt. Der Kaiser förderte archäologische Ausgrabungen in Alesia und ließ 1865 ein monumentales Standbild des Vercingetorix errichten - eine bewusste politische Botschaft in Zeiten wachsender Spannungen mit Preußen.
Der Mythos im Dienste der Nationenbildung
Die französische Republik übernahm später diese Interpretation und machte Vercingetorix zum Urvater der französischen Nation. Schulbücher priesen seinen Kampf für die Freiheit, wobei sie die historischen Fakten oft romantisch überhöhten. Diese patriotische Vereinnahmung zeigt, wie Geschichte für politische Zwecke instrumentalisiert werden kann. Interessanterweise beanspruchen heute auch regionale Bewegungen in der Auvergne und der Bretagne Vercingetorix als ihren kulturellen Ahnherrn.
Archäologische Spuren der gallo-römischen Zeit
Moderne archäologische Forschungen haben unser Verständnis der Epoche erheblich erweitert. Die Ausgrabungen in Bibracte, der Hauptstadt der Häduer und Treffpunkt des gallischen Widerstandsrats, geben Aufschluss über die hochentwickelte keltische Kultur. Man entdeckte:
- Komplexe Metallverarbeitungstechniken
- Ausgeklügeltes Münzwesen
- Beeindruckende Befestigungsanlagen
Diese Funde widerlegen das lange propagierte Bild der "primitiven Barbaren" und zeigen stattdessen eine vielfältige Zivilisation mit Handelsbeziehungen bis in den Mittelmeerraum.
Alesia heute: Zwischen Geschichte und Tourismus
Der Schauplatz von Vercingetorix' letzter Schlacht ist heute ein bedeutendes archäologisches Gelände mit Museumspark. Eine kontroverse Diskussion entzündet sich an der genauen Lokalisierung - einige Historiker bezweifeln, dass das offiziell anerkannte Alise-Sainte-Reine tatsächlich das historische Alesia ist. Ungeachtet dessen zieht der Ort jährlich tausende Besucher an, die die gewaltigen Belagerungswerke Caesars bestaunen können.
Vergleiche mit anderen antiken Freiheitskämpfern
Vercingetorix steht in einer Reihe mit anderen legendären Widerstandskämpfern gegen Rom:
- Arminius (Hermann der Cherusker), der 9 n. Chr. die Römer im Teutoburger Wald besiegte
- Boudicca, die britannische Königin, die 61 n. Chr. einen Aufstand anführte
- Spartakus, der Sklavenrebellion zwischen 73-71 v. Chr.
Doch während diese Figuren jeweils isolierte Erfolge erzielten, war Vercingetorix' Bewegung durch ihren territorialen Umfang und ihr politisches Programm einzigartig. Sein Versuch, eine gallische Nationalidentität zu schaffen, macht ihn zu einem besonders interessanten Forschungsobjekt.
Die Rolle der Druiden in der gallischen Gesellschaft
Oft übersehen wird die Bedeutung der druidischen Priesterkaste im Aufstand. Als Hüter der Tradition und Vermittler zwischen den Stämmen hatten sie erheblichen politischen Einfluss. Caesar berichtet von ihren langjährigen Ausbildungen und ihrer Zentralrolle in der gallischen Religion. Ihr möglicher Anteil an Vercingetorix' Strategie bleibt spekulativ, aber sicher ist, dass die Römer nach ihrem Sieg die Druiden systematisch verfolgten, da sie als Gefahr für die Romanisierung galten.
Vercingetorix in Literatur und Popkultur
Die Figur des gallischen Helden inspirierte zahlreiche künstlerische Werke:
- Den historischen Roman "Vercingétorix" von Camille Jullian (1901)
- Mehrere Filme und Fernsehproduktionen, darunter der französische Monumentalfilm "Vercingétorix" (2001)
- Comics wie "Asterix", wo er als ernsthafter Gegenpart zu den humorvollen Protagonisten auftritt
- Videospiele (z.B. "Civilization"-Reihe, "Total War: Rome II")
Diese Darstellungen schwanken zwischen historischem Realismus und nationalistischer Verklärung. Besonders der Asterix-Effekt hat das Bild des Vercingetorix in der Populärkultur stark geprägt - wenngleich stark vereinfacht.
Kritische Stimmen zur Heldenverehrung
Neuere Historiker fragen zunehmend kritisch nach den tatsächlichen Motiven und Methoden des gallischen Anführers:
- Waren seine Taktiken wirklich so innovativ?
- Wie freiwillig war die Unterstützung durch andere Stämme?
- Inwiefern profitierte er selbst von der römischen Präsenz in Gallien?
Diese differenzierte Betrachtung relativiert den Mythos, ohne die historische Bedeutung zu schmälern.
Die militarstrategischen Lehren aus dem gallischen Krieg
Militärakademien weltweit studieren noch heute Caesars Feldzüge in Gallien als Meisterstücke der Kriegskunst. Doch auch Vercingetorix' Ansätze bieten wertvolle Einsichten:
1. Die Effektivität asymmetrischer Kriegführung gegen überlegene Armeen
2. Die Bedeutung von Versorgungslinien in langen Konflikten
3. Die psychologische Komponente von Allianzbildung
Sein Scheitern lehrt zudem die Gefahren von:
- Unkoordinierten Angriffen
- Mangelnder langfristiger Planung
- Übertriebenem Vertrauen in befestigte Stellungen
Die Sprache als kulturelles Erbe
Obwohl Latein die keltischen Sprachen in Gallien verdrängte, haben sich bis heute zahlreiche keltische Wörter und Ortsnamen erhalten. Die französischen Begriffe "chemin" (Weg) oder "tonneau" (Fass) gehen auf gallische Wurzeln zurück. Diese sprachlichen Spuren bilden ein lebendiges Erbe der Kultur, die Vercingetorix zu verteidigen suchte.
Abschließende Würdigung eines widersprüchlichen Erbes
Vercingetorix bleibt eine Figur voller Widersprüche:
- Ein Führer, der Stämme einen konnte, aber nicht dauerhaft zusammenschweißen
- Ein Stratege mit bemerkenswerten Erfolgen, aber letztlicher Niederlage
- Eine historische Person, die zum Mythos wurde
Seine Geschichte wirft grundsätzliche Fragen auf:
- Kann militärischer Widerstand gegen ein Imperium erfolgreich sein?
- Wie entstehen nationale Identitäten?
- Inwieweit prägen spätere Interpretationen unser Verständnis der Vergangenheit?
Ein Vermächtnis für die Gegenwart
In einer Zeit, in der kulturelle Identitäten und Widerstand gegen Hegemonialmächte erneut an Bedeutung gewinnen, bietet das Schicksal Vercingetorix' relevante Denkanstöße. Sein Beispiel zeigt sowohl die Möglichkeiten als auch die Grenzen des Kampfes gegen übermächtige Gegner - eine Lehre, die über die Antike hinausreicht.
Letztlich steht Vercingetorix nicht nur für das gallische Gallien, sondern für den ewigen menschlichen Drang nach Selbstbestimmung. Auch wenn sein politisches Projekt scheiterte, hat sein symbolischer Widerstand die Jahrhunderte überdauert und inspiriert bis heute jene, die für Freiheit und kulturelle Eigenständigkeit eintreten.