Theodorus of Cyrene: The Enigmatic Mathematician of Ancient Greece
Introduction to Theodorus of Cyrene
Theodorus of Cyrene was an ancient Greek mathematician who lived during the 5th century BCE. Though much of his life remains shrouded in mystery, his contributions to mathematics, particularly in the field of geometry, have secured his place in history. A teacher of the renowned philosopher Plato, Theodorus played a pivotal role in shaping early Greek mathematical thought. His work on irrational numbers and the spiral that bears his name demonstrates his keen intellect and innovative thinking.
Cyrene, his birthplace, was a prosperous Greek colony in North Africa (modern-day Libya), known for its intellectual vibrancy. Theodorus' legacy, though fragmentary, offers a fascinating glimpse into the early development of mathematical theory and its intersection with philosophy.
Historical Context: The World of Theodorus
To understand Theodorus' significance, one must consider the intellectual milieu of ancient Greece during his time. The 5th century BCE was a period of immense cultural and scientific growth, often referred to as the Golden Age of Greece. Cities like Athens and Cyrene were hubs of learning, where mathematicians, philosophers, and scientists debated and expanded human knowledge.
Theodorus was a contemporary of prominent figures like Socrates and Hippocrates of Chios, working in an era when mathematics was transitioning from practical applications to theoretical exploration. The Pythagorean school, which had a strong influence on Theodorus, had already begun investigating the properties of numbers and geometric shapes, laying the groundwork for further discoveries.
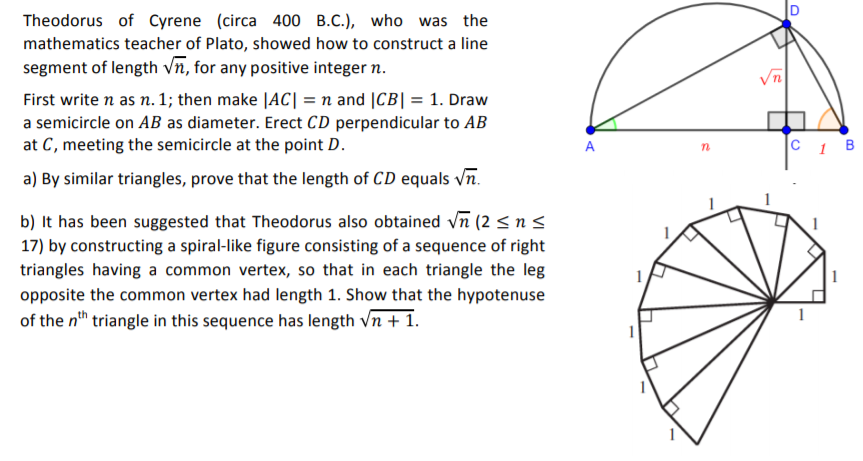
Theodorus and the Spiral
One of Theodorus' most famous contributions is the "Spiral of Theodorus," a geometric construction that demonstrates the sequential creation of right-angled triangles with hypotenuse lengths equal to the square roots of consecutive integers. This spiral, also known as the "Square Root Spiral," visually represents irrational numbers—a concept that was revolutionary at the time.
The spiral begins with an isosceles right triangle with legs of length 1. Subsequent triangles are added, each with one leg along the hypotenuse of the previous triangle and the other leg of length 1. The result is a visually striking figure that grows outward while maintaining a distinct mathematical pattern. This construction not only provided a way to visualize irrational numbers but also showcased Theodorus' ingenuity in geometric reasoning.
Contributions to the Theory of Irrational Numbers
Theodorus is often credited with advancing the understanding of irrational numbers, particularly through his work on square roots. According to Plato's dialogue "Theaetetus," Theodorus demonstrated the irrationality of the square roots of non-square integers from 3 up to 17. This was a significant step forward, as the concept of irrational numbers challenged the Pythagorean belief that all quantities could be expressed as ratios of integers.
His method of proving irrationality, though not fully detailed in historical records, likely involved geometric arguments similar to the classic proof of the irrationality of √2. Theodorus' work paved the way for later mathematicians, such as Eudoxus, to develop more rigorous theories of irrational magnitudes.
Teaching Plato and Philosophical Connections
Theodorus' influence extended beyond mathematics into philosophy, primarily through his relationship with Plato. In "Theaetetus," Plato portrays Theodorus as a respected teacher who engaged in conversations with Socrates and his students. This dialogue suggests that Theodorus was not only a mathematician but also a thinker deeply interested in epistemology and the nature of knowledge.
Plato's portrayal of Theodorus highlights the interdisciplinary nature of ancient Greek scholarship, where mathematics and philosophy were closely intertwined. Theodorus' mathematical insights likely informed Platonic ideas about the abstract nature of reality and the importance of mathematical forms.
Legacy and Later Interpretations
Despite the scarcity of surviving records, Theodorus' work has inspired mathematicians and scholars for centuries. The Spiral of Theodorus, in particular, continues to be a subject of study in both mathematics and art due to its aesthetic appeal and mathematical properties. Modern mathematicians have explored generalizations of the spiral, extending its principles to higher dimensions and more complex constructions.
Theodorus' contributions also underscore the collaborative and cumulative nature of mathematical progress. His investigations into irrational numbers built upon earlier Pythagorean discoveries and, in turn, influenced later developments in Greek mathematics. This interconnectedness reflects the enduring value of theoretical inquiry and the shared pursuit of knowledge across generations.
Theodorus’ Mathematical Methods and Techniques
Theodorus of Cyrene was renowned not only for his discoveries but also for his innovative methods in mathematics. Unlike many of his contemporaries, who relied heavily on verbal explanations and abstract reasoning, Theodorus may have employed visual and geometric demonstrations to illustrate mathematical concepts. His approach to proving the irrationality of square roots, for instance, likely involved constructing geometric figures—a technique that predates modern algebraic proofs.
Historians and mathematicians have attempted to reconstruct his methods based on references in Plato’s *Theaetetus*. One plausible reconstruction suggests that Theodorus used *anthyphairesis* (a Euclidean algorithm for ratios) to demonstrate irrationality. By systematically comparing magnitudes through reciprocal subtraction, he could show that certain lengths—such as √3 or √5—could not be expressed as simple ratios of whole numbers. This method aligns with the geometric tradition of ancient Greek mathematics, where proofs were often grounded in spatial reasoning rather than symbolic manipulation.
Theodorus and Pythagorean Influence
Theodorus’ work was deeply influenced by Pythagorean mathematics, though he also refined and challenged some of their doctrines. The Pythagoreans believed that all numbers could be expressed as ratios of integers, but the discovery of irrational magnitudes (such as the diagonal of a unit square) unsettled this worldview. Theodorus extended these investigations, moving beyond the well-known case of √2 to explore higher roots.
His insistence on demonstrating irrationality up to √17—rather than stopping at an earlier number—suggests a deliberate effort to establish a broader pattern. Some speculate that he may have encountered difficulties beyond √17, either due to increasing complexity or limitations in his methodology. Alternatively, he might have concluded that the pattern held universally, making further demonstrations unnecessary. Regardless, Theodorus’ willingness to push beyond established norms highlights his empirical rigor and intellectual independence.
The Spiral of Theodorus: Geometry and Artistic Legacy
The Spiral of Theodorus is more than just a mathematical curiosity; it represents a harmonious blend of logic and aesthetics. The spiral’s incremental growth, where each new triangle is built upon the hypotenuse of the previous one, creates a visually pleasing logarithmic spiral. This construction bridges arithmetic progression (adding unit legs) with geometric growth (expanding hypotenuse lengths).
In modern times, the spiral has been studied for its fractal-like properties and its connection to the distribution of prime numbers. Mathematicians have also explored variations, such as altering the angle between segments or using different starting dimensions. Artistic reinterpretations of the spiral appear in sculpture, digital art, and even architectural designs, demonstrating its enduring appeal as a symbol of mathematical beauty.
Theodorus’ Role in the Platonic Academy
Though Theodorus predates the formal establishment of Plato’s Academy, his teachings influenced its intellectual environment. Plato’s inclusion of Theodorus in *Theaetetus* underscores the mathematician’s reputation as both a scholar and a mentor. The dialogue portrays Theodorus as a figure who encouraged dialectical inquiry—aligning with Plato’s emphasis on collaborative learning.
Some scholars argue that Theodorus’ geometric methods may have inspired Plato’s concept of the “Divided Line,” where mathematical reasoning serves as a bridge between the physical and abstract realms. Whether directly or indirectly, Theodorus’ emphasis on systematic proof and visual reasoning resonated with Platonic metaphysics, reinforcing the interplay between mathematics and philosophy.
Lost Works and Speculations
No surviving texts authored by Theodorus exist today, leaving historians to piece together his contributions from secondhand accounts. Plato’s dialogues provide the most substantial references, but later commentators, such as Proclus and Iamblichus, also mention Theodorus in passing. These fragments suggest he may have written treatises on arithmetic, geometry, or even astronomy, though their contents remain speculative.
One intriguing possibility is that Theodorus compiled a “manual” of geometric constructions, possibly including compass-and-straightedge techniques for approximating irrational lengths. Such a work would have been invaluable to practitioners of *logistica* (applied calculation) and *theoretic arithmetic* (number theory). The absence of these texts leaves a frustrating gap in our understanding of his full impact.
Theodorus vs. Later Mathematicians
Theodorus’ contributions can be contrasted with those of later mathematicians like Eudoxus and Euclid. While Eudoxus developed a more general theory of proportions to handle irrational magnitudes, and Euclid systematized geometric knowledge in the *Elements*, Theodorus operated in an earlier, more exploratory phase. His work lacked the formal axiomatic structure of Euclid but showcased creative problem-solving that laid the groundwork for future rigor.
For example, Euclid’s proof of the irrationality of √2 (*Elements*, Book X) employs a reductio ad absurdum argument that may have evolved from Theodorus’ geometric demonstrations. Yet unlike Euclid, Theodorus likely relied on specific case-by-case constructions rather than universal proofs—a reflection of the developmental stage of Greek mathematics in the 5th century BCE.
Cultural Depictions and Modern Recognition
Despite his obscurity compared to figures like Euclid or Archimedes, Theodorus has occasionally been celebrated in literature and popular science. His spiral features in modern mathematics education as a tool for teaching irrational numbers, and his legacy is acknowledged in academic circles studying classical Greek mathematical thought.
Fictionalized accounts, such as historical novels set in ancient Greece, sometimes portray Theodorus as a “bridge” between Pythagoras and Plato—a figure embodying the transition from mystical numerology to deductive proof. While these depictions take artistic liberties, they reflect the fascination with his role in shaping early theoretical mathematics.
Unanswered Questions and Ongoing Research
Several mysteries surround Theodorus’ life and work. Why did he stop at √17? Did he travel to Athens, or did his interactions with Socrates occur in Cyrene? How did his North African origins influence his intellectual perspective? These questions remain open, but ongoing research in the history of mathematics continues to reassess his contributions.
Recent scholarship has explored the potential influence of Egyptian or Mesopotamian mathematics on his methods, given Cyrene’s geographic position as a crossroads of cultures. Others analyze the linguistic nuances in Plato’s dialogues to deduce Theodorus’ pedagogical style. Each new interpretation adds depth to our understanding of this enigmatic mathematician.
To be continued...
Theodorus’ Influence on the Development of Mathematics
The lasting impact of Theodorus of Cyrene extends far beyond his immediate contributions. While his name may not be as widely recognized as other mathematical luminaries, his work created essential stepping stones that facilitated later breakthroughs. Theodorus represents a crucial transition point between the mystical numerology of the Pythagoreans and the rigorous proof-based mathematics that would dominate Greek thought after Euclid. His willingness to confront the uncomfortable truth of irrational numbers helped shift mathematics from dogmatic belief to logical exploration.
Several key areas of mathematics trace their roots, at least partially, to Theodorus' investigations:
- The foundations of number theory
- The geometric representation of irrational quantities
- Early methods of mathematical proof
- The visualization of complex mathematical concepts
His spiral construction in particular has inspired modern mathematicians to explore its fractal properties and connections to number theory, revealing hidden depths to what might have originally been conceived as a simple teaching tool.
Theodorus in the History of Science Timeline
When we place Theodorus within the broader context of scientific development, his significance becomes even clearer. Living in the 5th century BCE, he occupies what we might call the "pre-Euclidean" period of Greek mathematics - a time when fundamental concepts were being discovered and defined. Consider the intellectual lineage:
1. Thales of Miletus (c. 624–546 BCE) - Introduced geometry to Greece
2. Pythagoras (c. 570–495 BCE) - Developed mathematical philosophy
3. Theodorus of Cyrene (c. 465–398 BCE) - Advanced irrational numbers
4. Eudoxus (c. 408–355 BCE) - Created theory of proportions
5. Euclid (c. 300 BCE) - Systematized geometry in Elements
This lineage shows Theodorus as a crucial link between the pioneering work of Pythagoras and the more sophisticated mathematics that followed. Without his contributions, the development of Greek mathematics - and thus Western mathematics as a whole - might have taken a different course.
Reconstructing Theodorus: Challenges for Historians
The fragmentary nature of evidence about Theodorus presents significant challenges for historians of mathematics. Unlike more famous figures whose works survived intact, Theodorus exists primarily in references from later writers, most notably Plato. This creates several persistent questions about his work and methods.
One major challenge involves distinguishing Theodorus' original contributions from those of his student Theaetetus, who Plato suggests may have generalized Theodorus' work on irrationals. Some scholars argue that important proofs attributed to Theodorus may actually represent Theaetetus' extensions of his teacher's ideas. The precise boundaries between their work may never be fully resolved.
The absence of Theodorus' own writings forces historians to employ several strategies of reconstruction:
- Close reading of Plato's dialogues
- Comparison with mathematical practices of his contemporaries
- Analysis of later commentators like Proclus
- Examination of archaeological evidence from Cyrene
Each of these approaches offers partial insights, but none provide a complete picture of Theodorus' mathematical practice. This has led to ongoing debates among historians about the nature and scope of his work.
Theodorus as a Teacher and Mentor
The available evidence suggests that Theodorus was not just an original thinker but also an influential educator. Plato's depiction in *Theaetetus* portrays him as a teacher willing to engage young students in serious mathematical discourse, a relative novelty in an era when advanced mathematics was often kept within exclusive circles.
Several aspects of Theodorus' pedagogical approach can be inferred:
1. He appears to have emphasized geometric demonstration over abstract reasoning
2. His spiral construction suggests a hands-on approach to mathematical concepts
3. He encouraged students to think through problems methodically
4. He was willing to challenge orthodox beliefs (like Pythagorean number theory)
This teaching style likely influenced Plato's approach to education at the Academy, particularly in its early years. Theodorus represents an important early example of a mathematician who saw teaching as integral to the development of mathematical knowledge, not merely as its transmission.
Mathematical Concepts Attributed to Theodorus
Beyond the spiral and irrational numbers, several other mathematical ideas have been associated with Theodorus, though with varying degrees of certainty. These possible contributions include:
1. Early Work on Square Roots: Theodorus may have developed systematic methods for approximating square roots, possibly building on earlier Babylonian techniques but giving them geometric foundations.
2. Constructible Numbers: His spiral essentially demonstrates the geometric construction of square roots, anticipating later Greek work on constructible numbers with compass and straightedge.
3. Prime Number Analysis: Some scholars suggest Theodorus may have noticed patterns in the irrationality of square roots related to prime numbers, though clear evidence is lacking.
4. Geometric Algebra: His approach to mathematics may have included early forms of geometric algebra, where algebraic relationships are expressed through geometric constructions.
While we cannot be certain how far Theodorus developed these concepts, their appearance in later Greek mathematics suggests he may have played a significant role in their early formulation.
Theodorus' Philosophical Implications
Theodorus' mathematical discoveries carried profound philosophical consequences that resonated through Greek thought. His demonstration of irrational numbers challenged fundamental assumptions about the nature of reality:
1. It undermined Pythagorean number mysticism by showing mathematical truths that defied whole-number ratios
2. It suggested that mathematical reality couldn't always be expressed in simple, rational terms
3. It raised questions about the relationship between discrete numbers and continuous magnitudes
4. It hinted at a mathematical universe more complex than previously imagined
These implications likely influenced Plato's own philosophical development, particularly his theory of forms. The existence of irrational magnitudes provided concrete evidence that perfect mathematical forms might differ substantially from physical appearances.
Theodorus' work also contributed to emerging distinctions between different types of mathematical knowledge:
- Practical arithmetic/computation
- Theoretical number studies
- Abstract geometric reasoning
- Proof methods and demonstration techniques
This differentiation would become crucial for the subsequent development of both mathematics and philosophy in the Hellenistic world.
Theodorus' Modern Relevance
While Theodorus lived over two millennia ago, his work remains surprisingly relevant to modern mathematics and education:
1. His spiral has become a teaching tool for introducing irrational numbers
2. His approach to geometric construction anticipates modern visual mathematics
3. His work with irrationals connects to current number theory research
4. His interdisciplinary approach (math and philosophy) mirrors modern STEM education
In our digital age, Theodorus' spiral has found new life in computer-generated art and algorithmic visualizations. Mathematicians continue to study its properties, finding new patterns and applications that Theodorus himself could never have imagined.
Final Assessment: Theodorus' Place in History
Theodorus of Cyrene occupies a unique and important position in the history of mathematics. Though less famous than his student Plato or his predecessor Pythagoras, his contributions were crucial in shaping the trajectory of mathematical thought. By bridging the gap between early Greek mathematics and the more systematic approaches that followed, Theodorus helped transform mathematics from a collection of observations into a discipline built on proof and logical structure.
His most significant achievements include:
- Advancing the understanding of irrational numbers
- Developing innovative geometric constructions (the spiral)
- Helping transition mathematical thought from mysticism to logic
- Influencing generations of mathematicians and philosophers
- Establishing teaching methods that emphasized understanding over memorization
While many details of his life and work remain lost to history, Theodorus' legacy endures in the fundamental concepts of mathematics that we still teach and explore today. In the grand narrative of mathematical discovery, he represents a crucial inflection point - the moment when Greek mathematics began its transformation from practical reckoning to theoretical science.
As we continue to uncover and reinterpret the fragments of ancient mathematical history, Theodorus' contributions remind us of the cumulative nature of mathematical knowledge. Each discovery builds upon those that came before, creating an unbroken chain of human intellectual achievement stretching back to thinkers like Theodorus and beyond. His story encourages us to value not just the famous names of history, but also the important transitional figures who helped lay the foundations for future breakthroughs.

Euclid: The Father of Geometry and His Timeless Legacy
Introduction to Euclid and His Mathematical Contributions
Euclid, often hailed as the Father of Geometry, was a Greek mathematician whose work laid the foundation for modern mathematics. Active around 300 BCE in Alexandria, Egypt, Euclid's most famous work, Elements, revolutionized the study of geometry, arithmetic, and number theory. His systematic approach, using axioms, postulates, and proofs, has influenced Western mathematics for over 2,000 years.
Early Life and Career of Euclid
Little is known about Euclid's personal life, but historical records suggest he studied at Plato's Academy in Athens before moving to Alexandria. Under the patronage of Ptolemy I Soter, Euclid taught at the Library of Alexandria, where he established a school around 300 BCE. His dedication to teaching and research led to the creation of about a dozen works, though most have been lost to time.
Euclid's Educational Philosophy
Euclid was known for his pragmatic and disciplined approach to education. One famous anecdote recounts his response to King Ptolemy, who asked if there was a simpler way to learn geometry. Euclid replied,
"There is no royal road to geometry."This statement underscores his belief in the necessity of rigorous study and dedication to master mathematical concepts.
The Structure and Impact of Elements
Elements is divided into 13 books, each addressing different aspects of mathematics. The first six books focus on plane geometry, while Books 7–10 delve into arithmetic and number theory. The remaining books explore advanced topics such as three-dimensional geometry and the properties of Platonic solids.
Key Theorems and Proofs in Elements
One of the most notable contributions in Elements is the proof of the infinitude of prime numbers. Euclid's methodical approach to proving geometric theorems set a precedent for future mathematicians. His work also includes a generalization of the Pythagorean theorem, further solidifying his legacy in the field of mathematics.
Euclid's Influence on Modern Mathematics
Euclid's axiomatic method has had a lasting impact on various fields, from algebra to computer science. His work standardized the use of logical proofs, which became a cornerstone of mathematical education. Even today, Euclidean geometry is taught in schools worldwide, highlighting its enduring relevance.
Cultural and Educational Significance
Beyond academia, Euclid's principles have influenced art, architecture, and technology. His teachings on Platonic solids have been visualized in animations and educational tools, making complex geometric concepts accessible to a broader audience. Additionally, his lost works, such as Fallacies, continue to spark interest among scholars studying logical reasoning.
Recent Developments and Scholarly Interest
In recent years, there has been a resurgence of interest in Euclid's methods, particularly in the fields of artificial intelligence and formal verification. A 2025 article reaffirmed Euclid's legacy, emphasizing the distinction between Euclidean geometry and non-Euclidean alternatives developed in the 19th century. Scholars continue to explore his teachings, highlighting their applicability in modern computational models.
Euclid's Enduring Legacy
Euclid's contributions to mathematics are unparalleled. His work has been translated into thousands of languages, ensuring its accessibility across cultures and generations. The 465 theorems and propositions in Elements remain a testament to his genius, inspiring mathematicians and educators alike to uphold the standards of rigorous proof and logical reasoning.
Euclid's Mathematical Methodology and Its Lasting Impact
Euclid's approach to mathematics was revolutionary for its time. He introduced a deductive system where each theorem was derived from a set of axioms and postulates. This methodology not only structured geometric principles but also provided a framework for logical reasoning that extended beyond mathematics into philosophy and science.
The Axiomatic System in Elements
The foundation of Euclid's Elements rests on five key postulates, the most famous being the Parallel Postulate. This postulate states that if a straight line intersects two other straight lines and the interior angles on the same side sum to less than 180 degrees, the two lines will eventually meet. This principle became a cornerstone of Euclidean geometry and was scrutinized for centuries, leading to the development of non-Euclidean geometries in the 19th century.
Influence on Scientific Thought
Euclid's emphasis on proof-based reasoning influenced prominent scientists like Isaac Newton, who modeled his Principia Mathematica after the structure of Elements. The systematic approach encouraged a culture of empirical validation, which became essential in the scientific revolution. Even today, Euclid's methods are echoed in computer algorithms and artificial intelligence, where logical deductions drive problem-solving processes.
Key Works and Lost Texts of Euclid
While Elements remains Euclid's most celebrated work, he authored several other texts that have either been lost or survive only in fragments. These works cover a range of topics, from optics to astronomy, showcasing his versatility as a mathematician and thinker.
Surviving Works Beyond Elements
- Data: A collection of geometric propositions that serve as a precursor to solving problems in Elements.
- Optics: One of the earliest surviving Greek treatises on perspective, exploring how vision and light interact with geometric forms.
- Phaenomena: A work on spherical astronomy, applying geometric principles to celestial movements.
Lost Works and Their Significance
Several of Euclid's texts have been lost to history, but their titles and descriptions provide insight into his broad intellectual pursuits. Notable lost works include:
- Conics: A study of conic sections, later expanded by Apollonius of Perga.
- Porisms: A work on geometric propositions that are intermediate between theorems and problems.
- Fallacies: A text on logical fallacies, which would have been invaluable in understanding ancient Greek reasoning.
These lost works highlight Euclid's role in shaping not just geometry but also logic, astronomy, and optics.
Euclid's Role in the Hellenistic World
Euclid's career flourished during the Hellenistic period, a time of immense intellectual growth in Alexandria. The city, under Ptolemy I Soter, became a hub for scholars, and the Library of Alexandria served as the epicenter of learning. Euclid's presence there solidified Alexandria's reputation as a center for mathematical and scientific advancement.
Collaboration and Intellectual Exchange
Euclid was part of a vibrant community of scholars who built upon each other's work. He drew inspiration from earlier mathematicians like Eudoxus and Theaetetus, refining their ideas into a cohesive system. His interactions with contemporaries, including Archimedes, further enriched his contributions, creating a legacy that transcended his lifetime.
The Alexandria School of Mathematics
The school Euclid established in Alexandria became a model for future academic institutions. It emphasized collaborative learning and rigorous debate, principles that are still valued in modern education. Students from across the Mediterranean flocked to Alexandria to study under Euclid, ensuring the dissemination of his ideas throughout the ancient world.
Euclid's Legacy in Modern Education
Euclid's influence extends far beyond ancient Greece. His teachings have been integrated into mathematics curricula worldwide, shaping how geometry is taught from primary schools to universities. The clarity and logical structure of Elements make it an enduring resource for educators and students alike.
Adaptations and Translations
Since its inception, Elements has been translated into numerous languages, ensuring its accessibility across cultures. Notable translations include:
- Arabic translations by scholars like Al-Hajjaj ibn Yusuf in the 9th century, which preserved Euclid's work during the Middle Ages.
- The first printed edition in Latin by Erhard Ratdolt in 1482, which marked the beginning of its widespread dissemination in Europe.
- Modern English translations, such as those by Sir Thomas Heath, which remain standard references in mathematical studies.
Euclid in Digital Age Learning
In the digital era, Euclid's principles have found new life through interactive software and online courses. Platforms like Khan Academy and GeoGebra use Euclid's geometric proofs to teach students dynamically. These tools allow learners to visualize theorems and engage with mathematics in ways that were unimaginable in Euclid's time, yet they remain rooted in his foundational methods.
Challenges and Criticisms of Euclid's Work
Despite its monumental influence, Euclid's work has not been without criticism. Scholars have debated the completeness and rigor of his axioms, particularly the Parallel Postulate, which led to the development of alternative geometric systems.
The Parallel Postulate Controversy
The Parallel Postulate was a subject of contention for centuries. Mathematicians attempted to prove it from the other postulates, but these efforts ultimately failed, leading to the discovery of non-Euclidean geometries by Carl Friedrich Gauss, János Bolyai, and Nikolai Lobachevsky in the 19th century. This development expanded the scope of geometry, showing that Euclid's system, while foundational, was not the only possible framework.
Modern Reevaluations
Contemporary mathematicians and historians continue to analyze Euclid's work, often highlighting its strengths and limitations. Some argue that Elements was more of a compilation of existing knowledge rather than a purely original work. However, Euclid's genius lay in his ability to synthesize and systematize these ideas into a coherent and teachable form, which remains his most significant contribution to mathematics.
Euclid's Influence on Non-Mathematical Fields
While Euclid is primarily celebrated for his contributions to mathematics, his influence extends into philosophy, art, and architecture. His systematic approach to problem-solving and logical reasoning has inspired thinkers across disciplines, demonstrating the universal applicability of his methods.
Philosophical Impact
Euclid's axiomatic method profoundly influenced Western philosophy, particularly in the development of deductive reasoning. Philosophers such as René Descartes and Baruch Spinoza adopted Euclid's structured approach in their works, using geometric principles as metaphors for logical argumentation. Descartes' Discourse on Method and Spinoza's Ethics both reflect the clarity and rigor of Euclid's Elements.
Art and Architecture
The principles of Euclidean geometry have been fundamental in art and architectural design for centuries. The use of symmetry, proportion, and geometric shapes in classical Greek and Roman architecture can be traced back to Euclid's teachings. During the Renaissance, artists like Leonardo da Vinci and architects such as Filippo Brunelleschi employed Euclidean principles to create works that emphasized harmony and balance.
Euclid in Popular Culture and Media
Euclid's legacy has permeated popular culture, appearing in literature, film, and even modern digital media. His name and ideas are often referenced to symbolize intellectual rigor and logical thinking.
Literary References
Euclid's influence can be seen in various literary works, where his name is synonymous with wisdom and precision. For example, in Edgar Allan Poe's The Purloined Letter, the detective C. Auguste Dupin uses a methodical approach reminiscent of Euclid's logical deductions. Similarly, Jorge Luis Borges references Euclid in his short stories, exploring themes of infinity and geometric perfection.
Film and Television
Euclid's concepts have also found their way into film and television, often used to convey complex ideas in an accessible manner. In the movie Good Will Hunting, the protagonist solves a challenging geometry problem inspired by Euclidean principles. Television shows like The Big Bang Theory frequently reference Euclid's theorems, highlighting their continued relevance in modern scientific discourse.
The Future of Euclidean Geometry
As technology advances, the applications of Euclidean geometry continue to expand. From computer graphics to space exploration, Euclid's principles remain foundational in various cutting-edge fields.
Computer Graphics and Virtual Reality
In the realm of computer graphics, Euclidean geometry is essential for rendering 3D models and virtual environments. Algorithms used in ray tracing and polygon modeling rely on Euclidean principles to create realistic images and animations. Virtual reality (VR) and augmented reality (AR) technologies also depend on geometric calculations to simulate immersive experiences, demonstrating Euclid's enduring impact on digital innovation.
Space Exploration and Astronomy
Euclid's contributions to spherical geometry have been crucial in the field of astronomy. Modern space missions, such as those conducted by NASA and ESA, use Euclidean principles to calculate trajectories and map celestial bodies. The Euclid Space Telescope, launched by the European Space Agency, is named in his honor and aims to explore the dark universe, further cementing his legacy in scientific exploration.
Conclusion: Euclid's Everlasting Legacy
Euclid's contributions to mathematics and beyond have left an indelible mark on human knowledge. His systematic approach to geometry, as outlined in Elements, has shaped education, science, and technology for over two millennia. From the classrooms of ancient Alexandria to the digital landscapes of the 21st century, Euclid's principles continue to inspire and guide intellectual pursuits.
Key Takeaways
- Foundational Work: Euclid's Elements remains one of the most influential mathematical texts in history, structuring geometry through axioms and proofs.
- Cross-Disciplinary Influence: His methods have impacted philosophy, art, architecture, and technology, demonstrating the versatility of his ideas.
- Modern Applications: Euclidean geometry is integral to computer graphics, space exploration, and artificial intelligence, showcasing its relevance in contemporary fields.
- Cultural Icon: Euclid's name and work are referenced in literature, film, and media, symbolizing intellectual rigor and logical thinking.
As we look to the future, Euclid's legacy serves as a reminder of the power of logical reasoning and systematic inquiry. His work continues to be a beacon for scholars, educators, and innovators, proving that the principles of geometry are not just confined to the past but are vital tools for shaping the future. In the words of Carl Friedrich Gauss,
"Mathematics is the queen of the sciences, and number theory is the queen of mathematics."Euclid, as the architect of this queen's foundation, remains an eternal figure in the pantheon of human achievement.



Euclid: The Father of Geometry and His Enduring Legacy
When we think of geometry, one name stands above all others: Euclid. Known as the Father of Geometry, Euclid's contributions have shaped mathematics for over two millennia. His seminal work, Elements, remains a cornerstone of mathematical education, influencing countless scholars and students. But who was Euclid, and how did his work transcend time? This article delves into the life, achievements, and lasting impact of Euclid, exploring his chronology and the profound legacy he left behind.
The Life and Times of Euclid
Euclid, or Ευκλείδης in Greek, lived during a pivotal period in history. While exact details of his life are scarce, historians place him in Alexandria, Egypt, around 300 BCE. This was during the Hellenistic period, a time of great intellectual flourishing under the reign of Ptolemy I. Euclid is believed to have founded the mathematical school at the Musaeum, an early precursor to modern universities.
Chronology and Historical Context
Determining Euclid's exact chronology is challenging due to the lack of contemporary records. Most estimates suggest he was born between 365–325 BCE and died around 265–300 BCE. These dates are derived from references by later writers, such as Proclus, a 5th-century CE philosopher who provided valuable insights into Euclid's life and work.
It's important to note that Euclid is distinct from Euclid of Megara, a philosopher who lived earlier. The confusion between the two highlights the need for careful historical analysis when studying ancient figures.
Alexandria: The Hub of Learning
Alexandria, during Euclid's time, was a vibrant center of learning and culture. The city's famous library, the Musaeum, attracted scholars from across the Greek world. Euclid's presence in Alexandria was instrumental in establishing the city as a hub for mathematical and scientific inquiry. His work at the Musaeum laid the groundwork for future generations of mathematicians and scientists.
Euclid's Magnum Opus: The Elements
Euclid's most famous work, Elements (Στοιχεία), is a 13-volume treatise that compiles and systematizes Greek geometry, number theory, and proofs. This monumental work has had an unparalleled impact on the field of mathematics, serving as the standard textbook for over 2,000 years.
The Structure and Content of Elements
Elements is divided into 13 books, each focusing on different aspects of mathematics. The first six books deal with plane geometry, covering topics such as triangles, circles, and parallel lines. Books seven through nine explore number theory, including prime numbers and the properties of integers. The final books delve into solid geometry, examining three-dimensional shapes and their properties.
One of the key features of Elements is its deductive and axiomatic approach. Euclid starts with a set of undefined terms, such as point and line, and five postulates, including the famous parallel postulate. From these foundations, he builds a comprehensive system of geometric proofs, demonstrating the power of logical reasoning.
The Parallel Postulate and Its Impact
The parallel postulate is one of the most debated and influential aspects of Euclid's work. It states that if a line segment intersects two straight lines forming two interior angles on the same side that sum to less than 180 degrees, the two lines, if extended indefinitely, will meet on that side. This postulate has sparked over 2,000 years of debate and ultimately led to the development of non-Euclidean geometries in the 19th century.
The parallel postulate's significance lies in its implications for the nature of space. Euclid's geometry assumes a flat, non-curved space, which became known as Euclidean geometry. However, the exploration of alternatives to this postulate by mathematicians like Lobachevsky and Riemann revolutionized our understanding of space and time, paving the way for Einstein's general relativity.
The Influence of Elements on Mathematics and Education
The impact of Elements on mathematics and education cannot be overstated. For centuries, it has been the go-to resource for students and scholars alike. Its influence extends beyond the realm of mathematics, shaping the way we think about logic, proof, and the structure of knowledge.
Global Reach and Translations
Elements has been translated into over 150 languages and has seen more than 2,000 editions published worldwide. This widespread dissemination is a testament to its universal appeal and enduring relevance. From ancient Greece to the Islamic world, the Renaissance, and modern times, Elements has been a constant presence in mathematical education.
Integration into Modern Curricula
Even today, Elements continues to play a crucial role in education. It is estimated that 70% of high school geometry curricula worldwide derive from Euclid's work. The principles and proofs outlined in Elements provide a solid foundation for students, helping them develop critical thinking and problem-solving skills.
The digital age has brought new opportunities for engaging with Elements. Projects like the Geometry Center have digitized the text, making it accessible to a global audience. Additionally, AI and computational tools are now being used to verify the proofs in Elements automatically, ensuring their accuracy and providing new insights into Euclid's methods.
Euclid's Legacy in Modern Mathematics
Euclid's influence extends far beyond the confines of classical geometry. His work has inspired generations of mathematicians and scientists, leading to groundbreaking discoveries and new fields of study.
Non-Euclidean Geometries and Beyond
The exploration of non-Euclidean geometries in the 19th and 20th centuries marked a significant departure from Euclid's assumptions. Mathematicians like Nikolai Lobachevsky and Bernhard Riemann developed alternative geometric systems that challenged the notion of a flat, Euclidean space. These innovations had profound implications for physics, particularly in the development of Einstein's theory of general relativity, which describes the curvature of spacetime.
Despite these advancements, Euclidean geometry remains a fundamental tool in many areas of mathematics and science. Its principles are applied in fields ranging from engineering to computer graphics, demonstrating the enduring relevance of Euclid's work.
Cultural and Philosophical Impact
Euclid's contributions have also had a significant impact on culture and philosophy. In ancient Greek thought, geometry was seen as a way to model the cosmic order, linking spatial and temporal concepts. This interplay between geometry and time is evident in the works of philosophers like Zeno, whose paradoxes questioned the nature of motion and infinity.
In modern times, there has been a renewed interest in Hellenic philosophy and its connection to Euclidean principles. Scholars and educators are exploring the links between Euclidean geometry and contemporary concepts in quantum physics and cosmology. This cultural revival highlights the timeless nature of Euclid's ideas and their continued relevance in today's world.
Conclusion: The Timeless Genius of Euclid
Euclid's legacy as the Father of Geometry is a testament to the power of human intellect and the enduring nature of mathematical truth. His work, Elements, has stood the test of time, shaping the course of mathematics and education for over two millennia. From the ancient streets of Alexandria to the digital classrooms of the 21st century, Euclid's principles continue to inspire and guide generations of learners.
As we reflect on Euclid's contributions, it is clear that his impact extends far beyond the realm of geometry. His deductive reasoning, axiomatic approach, and rigorous proofs have influenced fields as diverse as philosophy, physics, and computer science. In a world where knowledge is constantly evolving, Euclid's work remains a steadfast beacon of logical clarity and intellectual rigor.
In the next part of this article, we will delve deeper into the specific proofs and theorems presented in Elements, exploring their applications and the ways in which they have shaped modern mathematics. Stay tuned for a closer look at the timeless genius of Euclid and his enduring legacy.
The Mathematical Foundations of Euclid's Elements
Euclid's Elements is not just a collection of geometric principles; it is a masterclass in logical reasoning and deductive proof. The work begins with a set of definitions, postulates, and common notions that form the bedrock of Euclidean geometry. These foundational elements are crucial for understanding the structure and rigor of Euclid's approach.
Definitions, Postulates, and Common Notions
Euclid starts Elements with a series of definitions that establish the basic terms of geometry. These include fundamental concepts such as:
- Point: "That which has no part."
- Line: "Breadthless length."
- Straight line: "A line which lies evenly with the points on itself."
- Surface: "That which has length and breadth only."
- Angle: "The inclination to one another of two lines in a plane which meet one another and do not lie in a straight line."
Following the definitions, Euclid presents five postulates, which are assumptions specific to geometry:
- To draw a straight line from any point to any point.
- To produce a finite straight line continuously in a straight line.
- To describe a circle with any center and radius.
- That all right angles are equal to one another.
- The parallel postulate: That, if a straight line falling on two straight lines makes the interior angles on the same side less than two right angles, the two straight lines, if produced indefinitely, meet on that side on which the angles are less than two right angles.
In addition to the postulates, Euclid introduces five common notions, which are general principles applicable beyond geometry:
- Things which are equal to the same thing are also equal to one another.
- If equals are added to equals, the wholes are equal.
- If equals are subtracted from equals, the remainders are equal.
- Things which coincide with one another are equal to one another.
- The whole is greater than the part.
The Power of Deductive Reasoning
Euclid's use of deductive reasoning is one of the most significant aspects of Elements. Starting from his definitions, postulates, and common notions, Euclid systematically builds a series of propositions (theorems) through logical proof. This method ensures that each new concept is firmly grounded in the previous ones, creating a cohesive and rigorous system.
For example, the proof of the Pythagorean theorem (Proposition 47 in Book I) is a masterful demonstration of deductive reasoning. Euclid uses a series of geometric constructions and logical steps to show that in a right-angled triangle, the square on the hypotenuse is equal to the sum of the squares on the other two sides. This theorem has far-reaching applications in fields ranging from architecture to physics.
Key Theorems and Proofs in Euclid's Elements
Elements contains a wealth of theorems and proofs that have become foundational in mathematics. These propositions cover a wide range of topics, from basic geometric constructions to complex number theory. Below, we explore some of the most significant theorems and their applications.
Book I: Foundations of Plane Geometry
Book I of Elements establishes the basic principles of plane geometry. It includes essential theorems such as:
- Proposition 1: To construct an equilateral triangle on a given finite straight line.
- Proposition 5: In isosceles triangles, the angles at the base are equal to one another.
- Proposition 16: In any triangle, if one of the sides is produced, the exterior angle is greater than either of the interior and opposite angles.
- Proposition 32: In any triangle, the sum of the three interior angles is equal to two right angles.
- Proposition 47: The Pythagorean theorem.
These propositions are not merely academic exercises; they have practical applications in various fields. For instance, the principles of triangle geometry are used in navigation, astronomy, and engineering.
Book II: Geometric Algebra
Book II of Elements is often referred to as "geometric algebra" because it deals with the geometric interpretation of algebraic identities. This book includes propositions that are equivalent to algebraic formulas, such as:
- Proposition 4: If a straight line is cut at random, the square on the whole is equal to the squares on the segments and twice the rectangle contained by the segments. This is equivalent to the algebraic identity (a + b)² = a² + b² + 2ab.
- Proposition 5: If a straight line is cut into equal and unequal segments, the rectangle contained by the unequal segments of the whole together with the square on the straight line between the points of section is equal to the square on the half. This corresponds to the identity ab + ( (a - b)/2 )² = ( (a + b)/2 )².
These geometric interpretations of algebraic concepts were crucial in the development of algebraic geometry and laid the groundwork for future mathematical advancements.
Book III: Circles and Their Properties
Book III focuses on the properties of circles, including theorems about chords, tangents, and angles within circles. Key propositions include:
- Proposition 1: To find the center of a given circle.
- Proposition 3: If in a circle a straight line through the center bisects a straight line not through the center, it also cuts it at right angles; and if it cuts it at right angles, it also bisects it.
- Proposition 20: In a circle, the angle at the center is twice the angle at the circumference subtended by the same arc.
- Proposition 31: In a circle, the angle in a semicircle is a right angle.
These theorems have applications in optics, astronomy, and mechanical engineering, where the properties of circles and spherical shapes are essential.
Euclid's Influence on Islamic and Renaissance Mathematics
Euclid's Elements has had a profound impact on mathematical traditions beyond ancient Greece. During the Islamic Golden Age, scholars translated and expanded upon Euclid's work, preserving and advancing mathematical knowledge. Later, during the Renaissance, European mathematicians rediscovered and built upon these Islamic contributions, leading to a renaissance in mathematical thought.
The Islamic Golden Age and Euclid
In the 8th and 9th centuries, Islamic scholars began translating Greek mathematical texts, including Elements, into Arabic. These translations were crucial in preserving ancient knowledge and making it accessible to a broader audience. Notable Islamic mathematicians who contributed to the study and expansion of Euclidean geometry include:
- Al-Khwarizmi: Known as the "father of algebra," Al-Khwarizmi wrote commentaries on Euclid's work and developed algebraic methods that complemented geometric proofs.
- Omar Khayyam: A Persian mathematician and poet, Khayyam worked on the theory of parallel lines and contributed to the understanding of Euclid's fifth postulate.
- Nasir al-Din al-Tusi: Al-Tusi wrote extensive commentaries on Elements and made significant contributions to trigonometry and spherical geometry.
The Islamic world's engagement with Euclid's work ensured that his ideas were preserved and expanded upon, ultimately influencing the development of mathematics in Europe.
The Renaissance and the Revival of Euclidean Geometry
During the Renaissance, European scholars rediscovered the works of ancient Greek and Islamic mathematicians. The translation of Elements into Latin and vernacular languages played a pivotal role in the revival of mathematical studies. Key figures in this renaissance include:
- Fibonacci: An Italian mathematician who introduced the Hindu-Arabic numeral system to Europe and wrote extensively on Euclidean geometry.
- Regiomontanus: A German mathematician and astronomer who translated and commented on Elements, contributing to the development of trigonometry.
- Johannes Kepler: A German astronomer who used Euclidean geometry in his laws of planetary motion, bridging the gap between mathematics and astronomy.
The Renaissance period saw a renewed interest in the rigorous, logical approach of Euclidean geometry. This revival laid the groundwork for the scientific revolution and the development of modern mathematics.
The Enduring Relevance of Euclidean Geometry
Despite the advent of non-Euclidean geometries and modern mathematical theories, Euclidean geometry remains a fundamental tool in various fields. Its principles are applied in engineering, computer science, physics, and even art. The enduring relevance of Euclidean geometry is a testament to the timeless nature of Euclid's work.
Applications in Modern Engineering
Euclidean geometry is essential in civil engineering, where it is used to design structures, calculate dimensions, and ensure stability. For example, the principles of triangle geometry are applied in truss design, while the properties of circles are crucial in arch and dome construction.
In mechanical engineering, Euclidean geometry is used to design gears, levers, and other mechanical components. The precise calculations and geometric constructions outlined in Elements provide a solid foundation for these engineering applications.
Computer Graphics and Euclidean Geometry
The field of computer graphics relies heavily on Euclidean geometry. Algorithms for rendering 2D and 3D images, calculating distances, and determining intersections are all based on Euclidean principles. For instance, the Bresenham's line algorithm, used to draw lines on a raster grid, is rooted in the geometric concepts outlined by Euclid.
Additionally, computer-aided design (CAD) software uses Euclidean geometry to create precise models and simulations. Engineers and architects rely on these tools to design everything from buildings to aircraft, demonstrating the continued relevance of Euclid's work in modern technology.
Euclidean Geometry in Physics
In classical physics, Euclidean geometry is used to describe the motion of objects in Newtonian mechanics. The concepts of distance, velocity, and acceleration are all grounded in Euclidean space. Even in quantum mechanics, where non-Euclidean geometries play a role, Euclidean principles are used to model the behavior of particles in certain contexts.
Furthermore, Euclidean geometry is essential in optics, where it is used to study the behavior of light and design lenses. The principles of reflection and refraction, as described by Snell's law, are based on geometric constructions that trace their roots back to Euclid's Elements.
Conclusion: Euclid's Timeless Legacy
Euclid's Elements is more than just a historical artifact; it is a living testament to the power of logical reasoning and deductive proof. From its foundational definitions and postulates to its complex theorems and proofs, Elements has shaped the course of mathematics and influenced countless fields of study.
The impact of Euclid's work extends far beyond the ancient world. During the Islamic Golden Age, scholars preserved and expanded upon his ideas, ensuring their survival and transmission to future generations. The Renaissance saw a revival of Euclidean geometry, leading to the scientific revolution and the development of modern mathematics.
Today, Euclidean geometry remains a fundamental tool in engineering, computer science, physics, and beyond. Its principles are applied in cutting-edge technologies and continue to inspire new generations of mathematicians and scientists. As we look to the future, Euclid's legacy serves as a reminder of the enduring power of human intellect and the timeless nature of mathematical truth.
In the final part of this article, we will explore the cultural and philosophical impact of Euclid's work, as well as its influence on modern education and digital innovation. Stay tuned for a deeper dive into the lasting legacy of the Father of Geometry.
The Cultural and Philosophical Impact of Euclid's Work
Euclid's contributions extend beyond the realm of mathematics, influencing philosophy, culture, and even art. His rigorous approach to geometry has shaped the way we perceive space, time, and the structure of the universe. This section explores the broader cultural and philosophical implications of Euclid's work.
Geometry and Cosmic Order in Ancient Greek Thought
In ancient Greece, geometry was not merely a practical tool but a means of understanding the cosmic order. Philosophers like Plato and Aristotle saw geometric principles as reflections of the fundamental structure of reality. Plato, in particular, believed that geometric forms were the essence of the universe, with the physical world being an imperfect manifestation of these ideal forms.
Euclid's Elements embodied this philosophical perspective, presenting geometry as a systematic and logical framework for understanding the world. The interplay between geometry and time, as explored in Greek philosophy, is evident in concepts like Zeno's paradoxes, which questioned the nature of motion and infinity. Euclid's rigorous proofs provided a way to resolve these paradoxes, offering a structured approach to understanding spatial and temporal relationships.
The Interplay Between Geometry and Time
The relationship between geometry and time has been a recurring theme in philosophical and scientific thought. In ancient Greek philosophy, time was often conceptualized through geometric metaphors, such as the spiral and the wave. These metaphors were used to describe the cyclic nature of time and the motion of celestial bodies.
Euclid's work contributed to this interplay by providing a precise and logical framework for understanding spatial relationships. His geometric principles were applied to astronomical observations, helping to model the movements of planets and stars. This integration of geometry and time laid the groundwork for later advancements in astronomy and physics.
Euclid's Influence on Modern Education
The impact of Euclid's Elements on education cannot be overstated. For over 2,000 years, it has been a cornerstone of mathematical instruction, shaping the way students learn and understand geometry. This section explores the enduring role of Euclid's work in modern education.
The Role of Elements in Contemporary Curricula
Even in the digital age, Elements remains a fundamental resource in mathematics education. It is estimated that 70% of high school geometry curricula worldwide derive from Euclid's principles. The logical structure and deductive reasoning presented in Elements provide students with a solid foundation in critical thinking and problem-solving.
Modern textbooks often draw on Euclid's proofs and theorems, adapting them to contemporary teaching methods. For example, the Common Core State Standards in the United States include geometric concepts that trace their roots back to Euclid's work. Students learn to construct geometric proofs, solve problems using Euclidean principles, and apply these concepts to real-world scenarios.
Digital Innovations and Euclidean Geometry
The advent of digital technology has opened new avenues for engaging with Euclid's Elements. Online platforms and educational software have made it possible to visualize and interact with geometric concepts in ways that were previously unimaginable. Projects like the Geometry Center have digitized Elements, making it accessible to a global audience.
Furthermore, AI and computational tools are now being used to verify the proofs in Elements automatically. These tools not only ensure the accuracy of Euclid's work but also provide new insights into his methods. For instance, automated theorem provers can analyze the logical structure of Euclid's proofs, highlighting the elegance and rigor of his approach.
The Legacy of Euclid in Modern Mathematics
Euclid's influence extends far beyond classical geometry, shaping the development of modern mathematical theories and applications. This section explores the lasting impact of Euclid's work on contemporary mathematics and its various branches.
Non-Euclidean Geometries and Beyond
While Euclidean geometry assumes a flat, non-curved space, the exploration of non-Euclidean geometries in the 19th and 20th centuries revolutionized our understanding of space and time. Mathematicians like Nikolai Lobachevsky and Bernhard Riemann developed alternative geometric systems that challenged Euclid's assumptions.
These innovations had profound implications for physics, particularly in the development of Einstein's theory of general relativity. Einstein's work demonstrated that space and time are interconnected and can be curved by the presence of mass and energy. This revolutionary idea was built on the foundation of non-Euclidean geometries, which in turn were inspired by Euclid's original postulates.
Applications in Computer Science and Engineering
Euclidean geometry continues to play a crucial role in computer science and engineering. In computer graphics, algorithms for rendering images and calculating distances are based on Euclidean principles. For example, the Bresenham's line algorithm, used to draw lines on a raster grid, relies on the geometric concepts outlined by Euclid.
In engineering, Euclidean geometry is used to design structures, calculate dimensions, and ensure stability. The principles of triangle geometry are applied in truss design, while the properties of circles are crucial in arch and dome construction. Additionally, computer-aided design (CAD) software uses Euclidean geometry to create precise models and simulations, demonstrating the continued relevance of Euclid's work in modern technology.
The Future of Euclidean Geometry
As we look to the future, the principles of Euclidean geometry continue to inspire new generations of mathematicians, scientists, and educators. This section explores the potential future applications and advancements in Euclidean geometry, highlighting its enduring relevance in a rapidly evolving world.
Emerging Technologies and Euclidean Principles
The rise of emerging technologies such as virtual reality (VR) and augmented reality (AR) presents new opportunities for applying Euclidean geometry. These technologies rely on precise geometric calculations to create immersive and interactive environments. For example, VR systems use Euclidean principles to render 3D spaces and calculate the positions of virtual objects.
Additionally, advancements in robotics and autonomous systems are driving the need for sophisticated geometric algorithms. Robots use Euclidean geometry to navigate their environments, avoid obstacles, and perform complex tasks. The principles outlined in Elements provide a solid foundation for these applications, ensuring their accuracy and reliability.
Euclidean Geometry in Quantum Physics
In the realm of quantum physics, Euclidean geometry continues to play a role in modeling the behavior of particles and the structure of space-time. While non-Euclidean geometries are essential for describing the curvature of space-time, Euclidean principles are used to model the behavior of particles in certain contexts.
For instance, the path integral formulation of quantum mechanics, developed by Richard Feynman, relies on geometric concepts to describe the probabilities of particle interactions. These geometric principles are rooted in the foundational work of Euclid, demonstrating the enduring relevance of his ideas in cutting-edge scientific research.
Conclusion: The Enduring Legacy of Euclid
Euclid's Elements is a testament to the power of human intellect and the enduring nature of mathematical truth. From its foundational definitions and postulates to its complex theorems and proofs, Elements has shaped the course of mathematics and influenced countless fields of study. Its impact extends beyond the ancient world, influencing Islamic and Renaissance mathematics, and continuing to inspire modern education and technological advancements.
The cultural and philosophical implications of Euclid's work are profound, shaping our understanding of space, time, and the structure of the universe. His rigorous approach to geometry has provided a framework for logical reasoning and deductive proof, influencing fields as diverse as philosophy, physics, and computer science.
In the digital age, Euclid's principles continue to be a fundamental tool in education and technology. From computer graphics to engineering, the applications of Euclidean geometry are vast and varied. As we look to the future, the enduring relevance of Euclid's work serves as a reminder of the timeless nature of mathematical truth and the power of human intellect.
In conclusion, Euclid's legacy as the Father of Geometry is a testament to the enduring impact of his work. His contributions have shaped the course of mathematics and influenced countless fields of study, from ancient philosophy to modern technology. As we continue to explore the frontiers of knowledge, Euclid's principles remain a steadfast beacon of logical clarity and intellectual rigor, inspiring new generations of mathematicians, scientists, and educators.
Émile Picard: A Titan of Mathematical Innovation
Introduction
Émile Picard, a formidable name in the annals of mathematics, stands as a testament to human intellectual pursuit at its finest. An acclaimed French mathematician, Picard’s work left an indelible mark on the mathematical world, shaping the landscape of complex analysis and algebraic geometry in the late 19th and early 20th centuries. This first exploration into Picard’s illustrious career delves into his early life, foundational contributions, and the profound influence he wielded over future generations of mathematicians.
Early Life and Academic Journey
Born on July 24, 1856, in Paris, Charles Émile Picard grew up amidst the bustling intellectual milieu of France’s capital. His academic proclivity became apparent at an early age. Inspired by the mathematicians and scientists who preceded him, Picard pursued his studies with fervor. He entered the prestigious École Normale Supérieure in 1874, a breeding ground for many of France’s eminent scholars. Under the guidance of professors who recognized his innate talent, Picard immersed himself in the intricacies of mathematics, laying the groundwork for a career that would transform theoretical concepts into pragmatic solutions.
Groundbreaking Contributions to Mathematics
Picard’s early work focused on pure mathematics, where he gravitated towards analysis—a field that examines the properties and behaviors of mathematical functions. In this domain, his contributions were nothing short of revolutionary. Chief among these was the development of the "Picard Theorems," which are pivotal to the theory of complex functions. His first notable result, the Little Picard Theorem, states that every entire function that omits two or more values in the complex plane must be constant. This theorem was significant because it provided crucial insights into the nature of complex variables—a foundation for many subsequent discoveries in the field.
Following the Little Picard Theorem, he formulated the Great Picard Theorem, an even more powerful assertion. This theorem informs us that if a function defined in a neighborhood of a point omits three distinct values, it must be constant once extended to that point, assuming an essential singularity exists there. This work not only set a new standard in understanding complex functions but also in our comprehension of singularities—a critical concept in complex analysis.
Impact on Algebraic Geometry
Beyond his contributions to complex analysis, Picard made significant strides in the realm of algebraic geometry, a field concerned with zeros of multivariate polynomials. He was instrumental in developing methods to solve equations that appear in both algebra and geometry—a pursuit that marries the two disciplines. His work laid the groundwork for later developments in the field, influencing the techniques and perspectives that would prevail throughout the 20th century.
Picard’s exploration into linear algebraic groups and Galois theory enriched the mathematical community's understanding of how algebraic groups behave and interact. His work helped establish key connections between seemingly disparate areas of mathematics, offering a more unified approach to problem-solving and theoretical exploration.
The Honors and Accolades
Due to his pioneering work, Picard garnered numerous accolades. He became a member of the French Academy of Sciences at a notably young age, highlighting the academic community's recognition of his genius. His influence extended beyond France's borders, earning him international repute and invitations to lecture at prestigious institutions worldwide.
Moreover, his expertise was sought after in many governmental and scientific committees, allowing him to contribute to policy-making and the broader application of mathematics in technology and science. This involvement attests to the significance and applicability of his work, further cementing his legacy in the scientific domain.
Conclusion
Émile Picard’s early life and career set the stage for a history-changing journey in the world of mathematics. His work in complex analysis and algebraic geometry not only advanced theoretical understanding but also provided practical tools for future mathematical exploration. As we delve deeper into Picard's contributions, the vast scope of his influence and his lasting legacy continue to inspire awe and admiration within the scientific community. His journey speaks volumes, demonstrating how curiosity, coupled with rigorous analysis, can yield knowledge that transcends generations.
Mentorship and Influence on Future Mathematicians
Émile Picard's influence transcended his groundbreaking research; he was also a highly regarded mentor and educator. Throughout his academic career, Picard held teaching positions at several esteemed institutions, including the University of Paris (Sorbonne). His pedagogic style was distinguished by clarity and precision, traits that endeared him to students and colleagues alike. Picard’s lectures were known for their rigour and intellectual depth, sparking an enthusiasm for mathematics among his students, many of whom would go on to become influential mathematicians in their own right.
A measure of Picard’s legacy can be seen through the successes of his protégés, who carried forward his teachings and extended his methodologies. By fostering a collaborative environment, Picard positioned himself as a cornerstone in the academic community, influencing countless contemporaries and upcoming scholars. His ability to articulate complex theoretical concepts enabled many students to navigate the demanding landscape of high-level mathematics and make their own significant contributions.
Contributions to Mathematical Literature
In addition to his teaching duties, Émile Picard was a prolific writer who contributed extensively to mathematical literature. His publications are notable not just for their breadth, but also for their depth and clarity. Among his most celebrated works is the multi-volume "Traité d’Analyse," a treatise on analysis that served as a standard reference for many years. This opus demonstrated Picard's profound understanding of mathematical theory and his ability to distill complex ideas into accessible language.
Picard’s publications covered a wide array of topics, including differential equations, potential theory, and the theory of algebraic functions. Through these writings, Picard sought to bridge various mathematical concepts, thereby offering a more comprehensive framework for understanding advanced mathematical theories. His work also underscored the interconnectedness of mathematics, promoting a holistic approach that resonated with both his contemporaries and those who followed.
His Role in International Mathematical Community
Émile Picard’s reputation as a leading mathematician was not confined to France; it permeated the international mathematical community. This was due in part to his active participation in numerous international congresses and symposia, as well as his contributions to various scientific committees and organizations. Picard played crucial roles in organizing and chairing significant mathematical conferences, where he facilitated dialogues and collaborations that advanced global mathematical discourse.
His presence on the international stage was further cemented when he became the President of the International Mathematical Union (IMU), an organization dedicated to promoting international cooperation in mathematics. In this capacity, Picard advocated for open dialogue and the free exchange of ideas across borders, fostering an environment of collaboration that transcended national and cultural barriers.
Legacy in Mathematical Society
Picard’s legacy within the mathematical society is not merely a reflection of his academic contributions but also of his efforts to nourish and sustain the vibrancy of the mathematical community. Through his involvement with various mathematical societies, he championed initiatives that aimed to promote mathematics both as a profession and as a field of study. His presidency at the Société Mathématique de France and influential pieces in the society’s journal exemplify his commitment to the growth and dissemination of mathematical knowledge.
Furthermore, Picard was actively involved in educational reform within France, advocating for curricula that emphasized the importance of mathematical literacy, critical thinking, and problem-solving skills. His vision for mathematics education entailed not only producing mathematicians but also equipping students across disciplines with tools to apply mathematical reasoning within their specific fields.
Innovations and Their Lasting Impact
While Émile Picard's direct contributions to mathematics are profound, his indirect influence is equally significant. Innovations he introduced have had a broad and lasting impact, permeating many aspects of mathematical and scientific thought. His theorems and theories laid the foundation for future explorations in complex analysis and algebraic geometry, fields that have since evolved in fascinating and unexpected ways.
One area where Picard’s influence is especially notable is in the development of modern-day analysis and topology. Methods initially conceptualized by Picard have been expanded upon to explore new dimensions in these disciplines, impacting developments in both theoretical and applied mathematics. His work not only pushed the boundaries of what was conceivable at the time but also laid down pathways for the scientific community to venture into new territories.
Conclusion
The mathematical legacy of Émile Picard is a narrative defined by pioneering contributions, effective mentorship, and an unwavering dedication to academia and the global scientific community. His rich legacy is ensconced in his profound theoretical discoveries, the generations of mathematicians he nurtured, and the strides made in international cooperation through his leadership roles. As we reflect on his contributions, it is clear that Picard's work resonates well beyond his era, continuing to inspire and challenge contemporary mathematicians and scholars the world over. His life and work are testaments to the enduring power of intellectual inquiry and collaboration across the field of mathematics.
Picard and the Evolution of Mathematical Thought
The influence of Émile Picard extends beyond his tangible contributions to the theory of mathematics; he also played a pivotal role in the evolution of mathematical thought during a period marked by rapid scientific advancement. The late 19th and early 20th centuries were times of great transformation in the sciences, with burgeoning fields such as physics and engineering looking increasingly to mathematics for solutions to complex problems. Picard’s work contributed significantly to this exchange of ideas, providing critical insights that bridged theoretical mathematics and its practical applications.
One of the defining aspects of Picard’s impact was his ability to foresee and address the needs of both pure and applied mathematics. His approach underscored the importance of developing mathematical theories that, while abstract and challenging, could nonetheless elucidate real-world phenomena. This foresight paved the way for future collaborations between mathematicians and scientists, creating a lasting synergy that persists in contemporary research practices.
Recognition and Awards
Throughout his life, Émile Picard received numerous awards and honors that acknowledged his contributions to mathematics and the scientific community. His election to the French Academy of Sciences at an early age was one of many accolades marking his distinguished career. Furthermore, Picard was granted honorary memberships and fellowships by various esteemed scientific organizations across Europe and beyond, reflecting his widespread influence and the universal value of his work.
Among the most distinguished was Picard’s reception of the Poncelet Prize in 1886, awarded by the French Academy of Sciences for outstanding achievements in applied mathematics. Such recognition served not only as a personal accolade but also as an affirmation of the broader significance of his contributions to the mathematical world and their impact on allied scientific disciplines.
Challenges and Perseverance
In the realm of great achievements, it is easy to overlook the challenges that pave the way to innovation and discovery. Like many intellectual pioneers, Picard encountered obstacles in his pursuit of mathematical understanding. During his lifetime, the field of mathematics was undergoing substantial transformations, with new theories and methodologies constantly evolving. Navigating these breakthroughs required not only mathematical skill but also adaptability and a commitment to lifelong learning.
Despite these challenges, Picard demonstrated an indomitable spirit, continually revising and expanding his theoretical frameworks to accommodate emerging knowledge. His perseverance in the face of adversity not only advanced his field but also set an example for those who followed, highlighting the importance of resilience in the pursuit of scientific inquiry.
Picard’s Influence on Modern Mathematics
The enduring impact of Émile Picard on modern mathematics cannot be overstated. His theorems and methodologies form a cornerstone for many advanced studies in complex analysis and topology. Today, his work is cited in both theoretical explorations and practical applications, from advanced computational models to cutting-edge research in physics and engineering. Mathematicians continue to draw inspiration from Picard’s techniques, which provide valuable insights into the structure and behavior of functions and their singularities.
Picard’s work has also influenced various branches of mathematics beyond his immediate areas of focus. His contributions to algebraic geometry, for example, have informed approaches in areas like cryptography, coding theory, and even aspects of quantum computing, showcasing the versatility and broad applicability of his insights.
Picard’s Enduring Legacy
In reflecting on the legacy of Émile Picard, it becomes clear that his impact transcends the confines of mathematics. His work exemplifies the notion that theoretical exploration, driven by curiosity and meticulous analysis, can yield results that stand the test of time. Picard’s lasting legacy is not only found in the theorems that bear his name but also in the spirit of inquiry and collaboration that he championed throughout his career.
His life and work continue to inspire generations of mathematicians and scientists to probe deeper, think critically, and embrace the interconnected nature of scientific disciplines. The intellectual paths he forged serve as a guiding light for those who seek to push the boundaries of human understanding and contribute meaningfully to the body of scientific knowledge.
Conclusion
The story of Émile Picard is one of brilliance, perseverance, and far-reaching influence. His remarkable contributions to mathematics have solidified his place among the great thinkers of his time, leaving a legacy that resonates throughout the scientific world. From his groundbreaking theorems to his role as a mentor and leader, Picard's influence is evident in both the historical progression and future potential of mathematical study. As we honor his memory, we celebrate not only his achievements but the ongoing journey of exploration and discovery that he so passionately embodied. Through his life's work, Picard reminds us of the boundless possibilities held within the pursuit of knowledge, inspiring future generations to carry forward the torch of scientific exploration.

